方程式赛车滚子链链轮静强度分析计算方法

于明杰，黎奉常

（武汉理工大学 汽车工程学院，湖北 武汉430070）

1 引言

链传动是一种挠性传动，它由链条和链轮组成，过链轮轮齿与链条链节的啮合传递动力和运动[1]。相较于带传动，其传动时无打滑现象，安装和制造成本较低，这对于对传动精确度要求较高、成本控制较为严格的方程式赛车是一个不错的选择。而链轮作为赛车传动系统较为关键的零部件，为了实现轻量化，近年来在进行设计时多采用铝（7075-T6）材料，而该种铝合金相对于通常采用的40Cr 合金钢硬度较低，抗冲击和抗磨损性能比较差，相对于采用合金钢的链条更加容易损坏，所以着重对链轮进行分析。

近年来，国内外对赛车各零部件进行了大量轻量化的探索，其中不乏采用拓扑优化方法进行链轮的轻量化处理，而拓扑优化的基础是对零部件进行准确的应力和应变分析。对于有限元软件，在分析时链轮与链节、链节与链节之间存在着许多的接触关系，这些接触关系组成了一个多接触系统，其力学求解十分复杂。研究表明，当具有多接触约束的机械系统在进行仿真分析的时候，往往存在着明显的计算效率低下的现象，尤其在分析模型比较庞大的时候，甚至会导致求解失败[2]。针对这一问题，蒲明辉等人[3]使用Adams 虚拟样机技术，将链传动动力学分析中链节之间的约束以柔性连接代替刚性连接，缩短了仿真时间，提高了仿真效率。

本文基于理论推导，简化了链轮链条的受力模型，将简化后的结果应用于链轮的静力分析中，通过比较多接触模型和简化后的力分析模型，验证力分析模型的正确性以及计算效率优越性。

2 方程式赛车滚子链传动特点

在方程式赛车链传动系统中，由于比赛项目的多样——直线加速、8 字绕环、高速避障、耐久，链轮需要承受直线加速弹射起步时的冲击载荷以及高速避障与耐久时的动态载荷。本文着重把赛车弹射起步时的冲击载荷转化为静载荷进行分析。

3 链传动的简化力分析模型

在链轮与链节的滚子达到平衡过程中，每个链节的受力并不是孤立进行的。每个链节存在类似的平衡状态，只有逐个达到平衡后，各链节才能停止上移，达到啮合平衡状态[4]。

链轮平衡时各啮合链节的受力平衡简图如图1 所示。

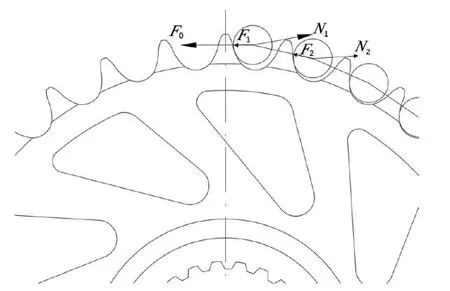
图1 各啮合链节的受力平衡简图

由上述引文对刮板输送机链轮和链节的分析可知，滚子链链轮和刮板输送机链轮的受力形式基本相同，所以将引文的公式进行简化后，啮合力的变化方程为：

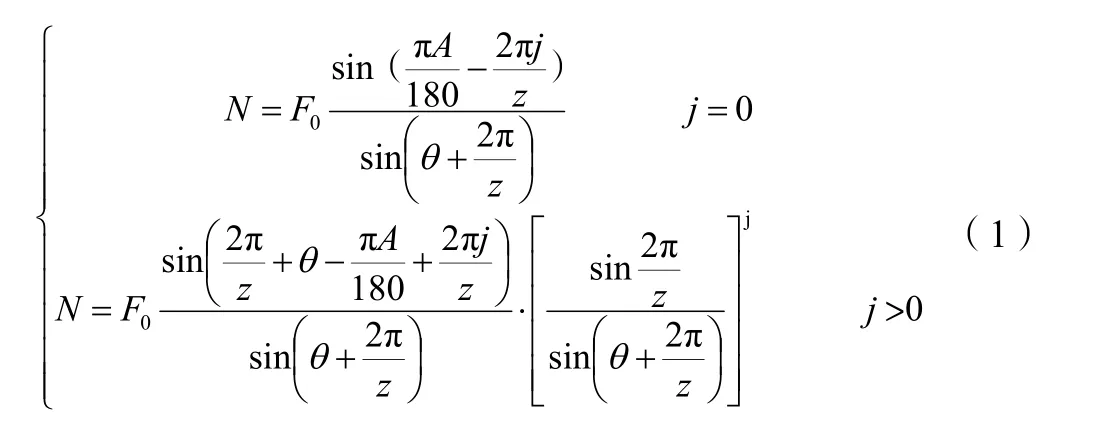
式（1）中：A为链轮的旋转角度，°；z为链轮齿数；j=floor（Az/360）；θ为齿形半角，rad。

4 链传动简化模型与多接触模型的对比分析

近年来，中国方程式赛车传动系统多采用密度较小、综合性能较好的7075 铝合金材料，可以满足使用要求。仿真采用的是武汉理工大学燃油方程式赛车队2019 赛季使用的链轮，该链轮为32 齿滚子链链轮。

表1 为链轮基本尺寸参数。

表1 大链轮参数表

4.1 大链轮的建模

大链轮的三维模型如图2 所示。

图2 大链轮的三维模型

按照国家标准GB/T 1243—1997 在三维建模软件Catia中分别构建链轮和链条的三维立体模型（其中链条为采购件，按照实际尺寸建模）。其中，齿形按照标准以及配合链条实际尺寸进行建模，而花键则参考德雷克斯勒技术文件上的花键尺寸进行建模，外形则进一步参考链轮所在位置具体尺寸，满足2019 年中国大学生方程式汽车大赛规则中链板的宽度至少为链条最宽处宽度的3 倍，且链条在链条中心线向左和向右各1.5 倍链条宽度范围内，都能被防护罩防护。

4.2 受力模型的进一步简化

对于32 齿链轮，先将每个齿上的力进行简化。赛车实际行驶时，遇到的工况非常复杂，但可主要分为匀速、弹射起步、紧急制动3 个工况。经过分析，发现大链轮的危险工况为弹射起步工况，集成变速箱将力矩传递给小链轮，小链轮通过链条将力矩传递给大链轮，在起步瞬间，可以假设大链轮静止，承受来自链条的全部拉力[5]。

第一个齿啮合力最大时其他齿啮合力并非最大，但因其为循环工况，指定第一个齿啮合力最大即可。给定紧边张力F0=7 214 N 在j=0 时计算得第一个齿啮合力最大时链轮的转角为A=11.25°，则在这种情况下（齿形半角θ=15°），算得各齿所受啮合力的大小。N1=0.438 6F0=3 164 N，N2=0.246 2F0=1 776 N，N3=0.108 0F0=779 N，N4=0.047 4F0=342 N。

第一个齿受力最大时的转角关系如表2 所示。

表2 第一个齿受力最大时的转角关系

4.3 链轮装配体的有限元分析模型

链轮与链条的材料属性表如表3 所示。

表3 链轮与链条的材料属性表

通过Catia 与ANSYS 的数据接口导入ANSYS 软件进行有限元分析。在Engineering Data 中建立材料7075 铝，并输入弹性模量7.20×1010Pa、泊松比0.330。利用CAD/CAE 之间接口，将大链轮与链条装配的CATProduct 三维数模导入ANSYS Workbench 软件中。大链轮与链条的约束采用ANSYS 自动生成。采用网格密度为1.5 mm 的四面体网格。在大链轮花键的一端施加Fix Support 约束[6]。

由上面的计算结果可知，第4 个齿的啮合力N4=0.047 4F0=342 N，对比第1 个齿N1=0.438 6F0=3 164 N，两者相差一个数量级，所以没有必要对后面的齿的啮合力进行计算。

对于力简化模型，直接在链轮前四个齿的工作段上添加F1、F2、F3、F4四个力（后面的轮齿受力较小，分析意义不大）。

而对于多接触分析模型，定义链轮与链节、链节与链节之间的接触形式为No Separation，然后在第一个链节上施加作用力F0=7 214 N。

两种分析模型的边界条件如图3 和图4 所示。有限元分析结果如图5 和图6 所示。

图3 简化力分析模型边界条件

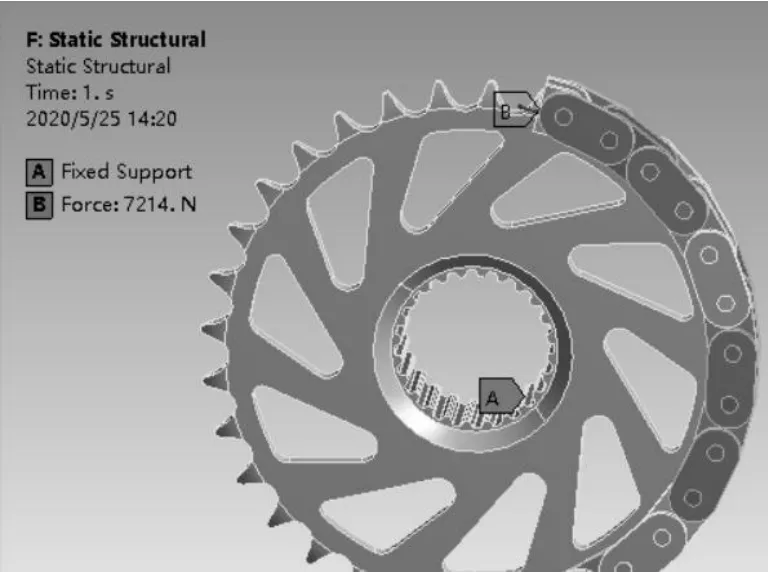
图4 多接触模型边界条件

图5 简化力模型安全系数

图6 多接触模型安全系数

由上图可知，简化力学模型分析方法最终得出的安全系数值与多接触模型得出的结果相差3.6%，在误差可接受范围内。对于计算效率，由于多接触模型的计算复杂度太大，计算结果未能完全收敛以达到更加精确的地步，而简化力分析模型只有一个实体和较少的边界条件，计算结果较快地收敛，更快地得到了计算结果。

4.4 实验分析

将加工后的模型装配到赛车上，并进行多次跑动试验。大链轮实物和大链轮实际使用分别如图7 和图8 所示。由图7、图8 可知，链轮装配到赛车上后，除了有轻微的磨损，没有缺齿等严重损伤。在训练过程中，未发现其他异常现象，说明其静力特征满足要求。

5 结论

建立了链轮的简化力分析模型，并结合有限元分析校核其静强度。对比简化力分析模型和多接触链轮模型的有限元分析结果，相互验证合理，结合实际证明其满足使用要求。虽然进行了静强度分析，但由于赛车动态运行过程中的受力情况更为复杂，加上链轮磨损与金属疲劳的因素，并不能仅根据静强度分析保证其长期可靠性。下一步的工作则是着重分析链轮在长时间工作下的失效形式。

图7 大链轮实物

图8 大链轮实际使用