耦合Riccati方程数值迭代方法
, , ,
(湖南工业大学 理学院,湖南 株洲 412007)
1 研究背景
本文考虑一类耦合非对称代数Riccati方程(coupled nonsymmetric algebraic Riccati equation,CNARE)
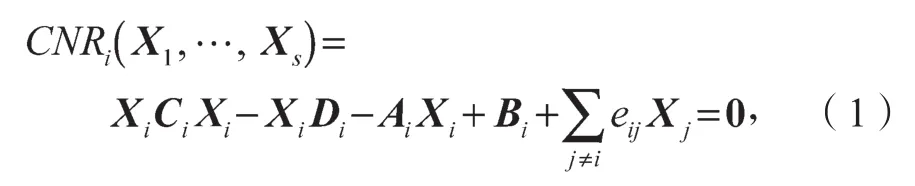
式中:Xi∈Rn×n为方程的解,i,j∈U={1,2,…,s},其中s是大于1的整数;
Ai∈Rm×m,Bi∈Rm×n,Ci∈Rn×m,Di∈Rm×n为方程的系数矩阵;
eij为非负常量,且满足列和为1。
此类方程在粒子输运理论[1-2]、控制理论[3]和马尔可夫链[4-6]等领域中有着广泛而深入的应用。在实际建模中,人们对此类方程感兴趣的是其具有实际意义的最小非负解。特别地,当s=1时,耦合方程(1)还原成非对称Riccati方程
Q(X)=XCX-XD-AX+B=0。
其最小非负解的存在性和相关数值求解方法已经得到了充分的研究[7]。
为了更好地研究更广泛的耦合方程(1)的最小非负解的存在性和相关的数值迭代方法,本文将耦合方程(1)写成如下统一形式:

El为只有(i,j)块和(j,i)块分别为eijIn和ejiIn,其余块都为0的矩阵,共有p=s(s-1)/2个。
2 定义与预备定理
对任何矩阵A和B,A>B(A≥B)表示矩阵A中所有元素大于(大于或等于)矩阵B中的所有元素,特别地若A≥0,则称A为非负矩阵。
定义1[8-9]若矩阵A∈Rn×n的非对角元非正,则称A为Z-矩阵。
任何Z-矩阵都可写成sI-B,其中B≥0。
定义2[8-9]若s≥ρ(B),Z-矩阵A=sI-B(B≥0)称为M-矩阵。特别地,若s=ρ(B),称A为奇异的M-矩阵;若s>ρ(B),称A为非奇异的M-矩阵,其中ρ(B)为B谱半径。
定理1[10]对Z-矩阵A,下述命题等价:
1)A是非奇异的M-矩阵;
2)A是非奇异矩阵且满足A-1≥0;
3)存在某一向量v>0使Av>0;
4)A的所有特征值都有正的实部。
定理2[10]设A∈Rn×n是一个M-矩阵,如果B∈Rn×n中的元素满足关系bii≥aii,aij≤bij≤0,i≠j,1≤i,j≤n,则B也是一个M-矩阵。
本文假设耦合方程(2)满足如下条件:
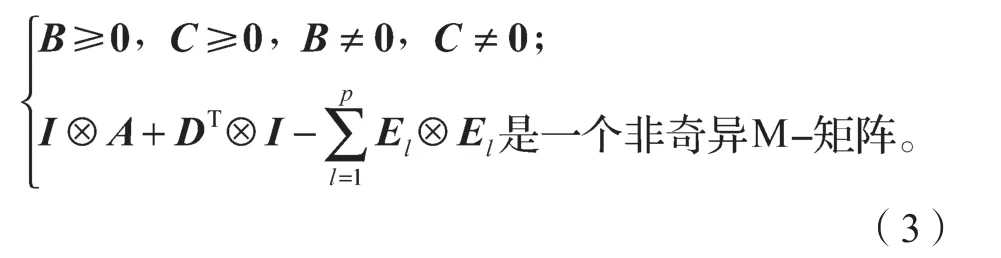
注1 由克罗内克积的性质可知,当且仅当A,D和E是Z-矩阵时IA+DTI-∑ElEl也是Z-矩阵。在不混淆的情况下,本文从此开始省略求和符号∑的上下标。
3 迭代方法
3.1 牛顿迭代
考虑对耦合方程(2)的牛顿迭代法。假设Rm×n是Banach空间,R是Riccati函数在空间Rm×n到自身的映射,则其Frechet导数为[12-13]
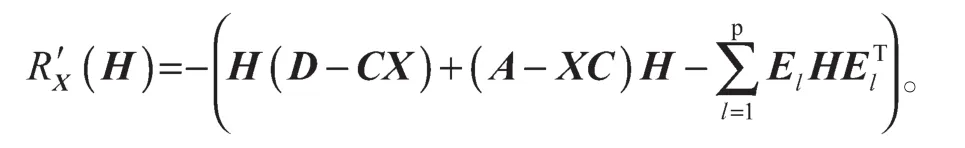
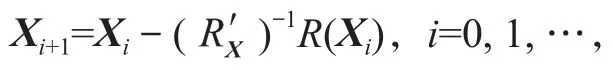
则求解耦合方程(2)等价于如下迭代格式:
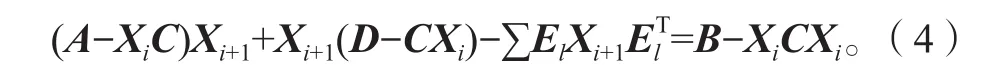
对上述牛顿迭代格式有如下收敛性定理3。
定理3如果存在一个非负矩阵X使得方程(2)满足R(X)≤0,且条件(3)成立,则对上述非负矩阵X,一定存在(2)的一个非负解S使得S≤X,特别地,S是方程(2)的最小非负解。此外,对于牛顿迭代格式(4),当X0=0时,序列{Xi}是适定的,并满足
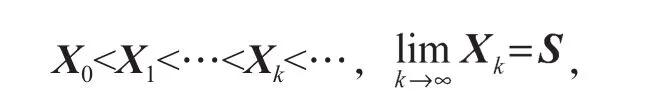
而且矩阵
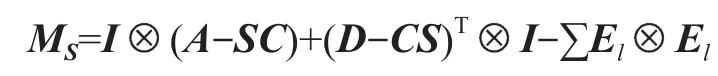
也是一个M-矩阵。
证明设X为任意一个非负矩阵,使得
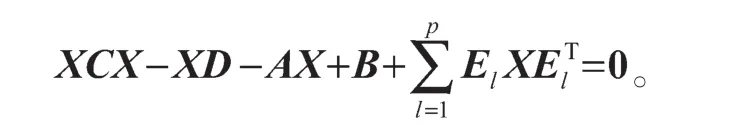
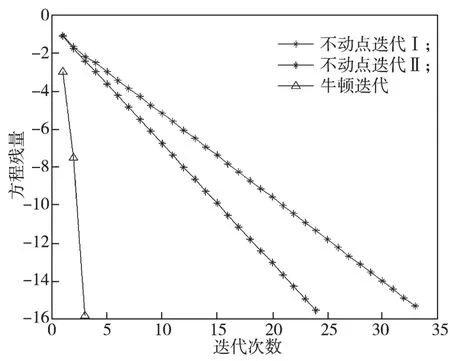
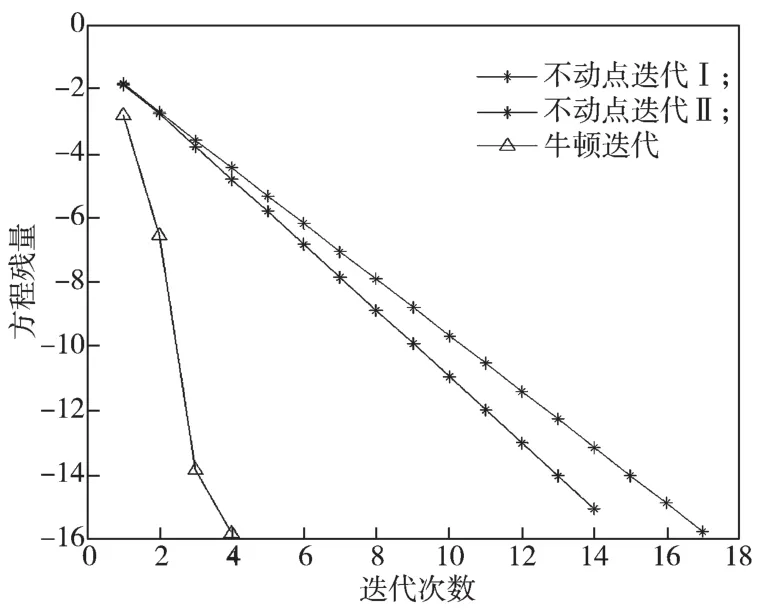
对于牛顿迭代式(4),用数学归纳法证明对所有的k满足:Xk 是非奇异M-矩阵。 当X0=0时,有 即有 式中vec运算是将矩阵的列转化成一个长矢量[14]。 设当k=i≥0时归纳假设成立。 由式(2)和式(4)得 (A-XiC)(Xi+1-X)+(Xi+1-X)(D-CXi)-∑El(Xi+1-X)El= B-XiCXi-AX+XiCX-XD+XCXi=-(Xi-X)C(Xi-X)。 因为Xi 另一方面,由式(4)得 由式(2)和式(6)可得 (A-Xi+1C)(Xi+1-X)+(Xi+1-X)(D-CXi+1)-∑El(Xi+1-X)El= -(Xi+1-Xi)C(Xi+1-Xi)-(Xi+1-X)C(Xi+1-X)<0。即有 因此由定理1中的命题3)可知, 是非奇异M-矩阵。 再次由式(4)和式(6)可得 因此有Xi+1 最后,假设对所有的i≥0,非奇异M-矩阵 注2 上述结果与文献[13]中定理9.1.1有相似的性质。 将耦合方程(2)中系数矩阵A、D进行分解,写成 A=A1-A2,D=D1-D2, 且满足A2,D2≥0,A1,D1是Z-矩阵。则耦合方程(2)变为 其中线性算子 定理4如果对于非负矩阵X,R(X)≤0,则由不动点迭代式(8)给定初始迭代点X0=0,对任意的k≥1有 证明对不动点迭代式(8),采用数学归纳法证明 Xk 当k=0时,有 这个方程等价于 设当k=i≥0时归纳假设成立。 由式(7)和式(10)得 另一方面,由式(10)得 因此有Xi+1 本章通过数值实验验证牛顿迭代和不动点迭代的收敛理论,并比较两种迭代方法的数值表现。计算采用Matlab 14a编程,其机器精度为2-53,约为2.2e-16。在不动点迭代法中,矩阵A1和D1分别为矩阵A和D的对角矩阵和下三角矩阵,记为不动点迭代I和不动点迭代II。当两类算法方程残量小于10-15时,终止算法。方程残量的计算公式为 例1考虑一类耦合非对称代数Riccati方程(1),其对应的系数矩阵为 解分别采用牛顿迭代和两类不动点迭代方法编程求解上述问题。当所有算法终止后,将迭代次数和方程残量列于表1中。 表1 例1中牛顿迭代与不动点迭代数值表现Table1 Numerical representation of Newton’s method and two fixed-point iterations in example 1 从表1可以看出,迭代终止时,牛顿法迭代次数比不动点迭代I和不动点迭代II少很多。迭代终止时,牛顿法迭代能获得比不动点迭代I和不动点迭代II更小的方程残量。对两种不动点迭代而言,不动点迭代II的迭代次数比不动点迭代I少,其获得的方程残量也比不动点迭代I更小。实际上,不动点迭代I等价于Jacobi迭代,而不动点迭代II等价于Gauss-Seidel迭代。 图1为3种迭代方法方程残量的历史图。从图中可以看出,牛顿迭代法是二次收敛,而两种不动点迭代都是线性收敛,但不动点迭代II比不动点迭代I在每步都能获得更小的方程残量。 图1 例1中牛顿迭代与不动点迭代方程残量历史图Fig.1 Residual history diagram for Newton’s method and fixed-point iteration equation in example 1 例2考虑一类耦合非对称代数Riccati方程(1),其对应的系数矩阵为 解与例1类似,分别采用牛顿迭代和两类不动点迭代方法编程求解上述问题。当所有算法终止后,将迭代次数和方程残量列于表2中。 表2 例2中牛顿迭代与不动点迭代数值表现Table2 Numerical representation of Newton’s method and two fixed-point iterations in example 2 从表2可以得出,当迭代终止时,牛顿法所需的迭代次数比不动点迭代要少得多,而且能获得更小的方程残量。 图2为3种迭代方法方程残量的历史图。从图中可以看出牛顿法迭代是二次收敛的,而2种不动点迭代都是线性收敛。 图2 例2中牛顿迭代与不动点迭代方程残量历史图Fig.2 Residual history diagram for Newton’s method and fixed-point iteration equations in example 2 本文采用牛顿迭代法和不动点迭代法求解一类非对称耦合的Riccati方程。在一定条件下证明了这两种迭代方法单调收敛到具有实际意义的最小非负解,数值实验验证了提出方法的有效性。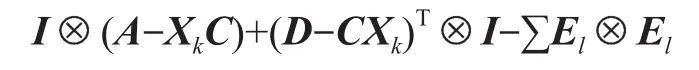
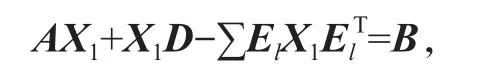
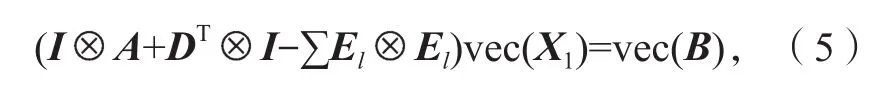
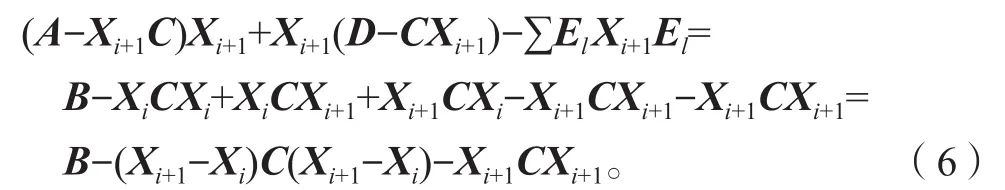
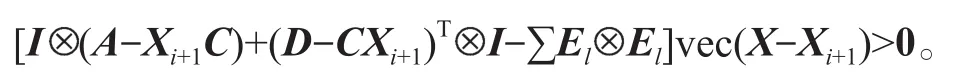
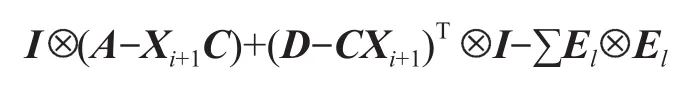
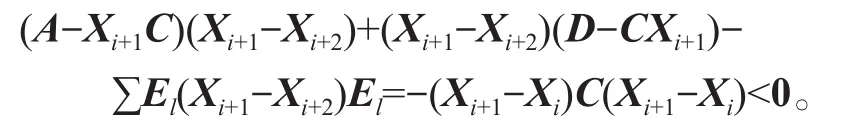
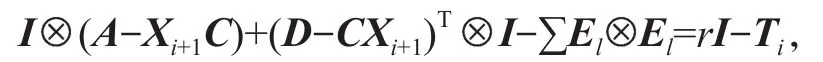
3.2 不动点迭代
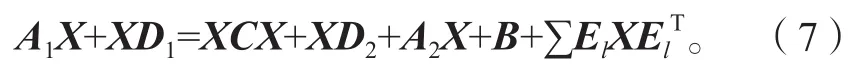
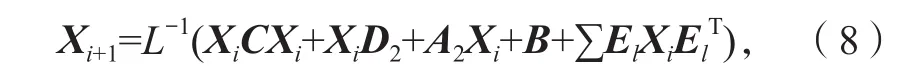
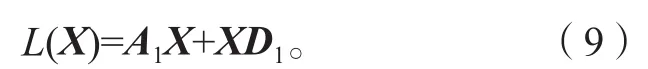
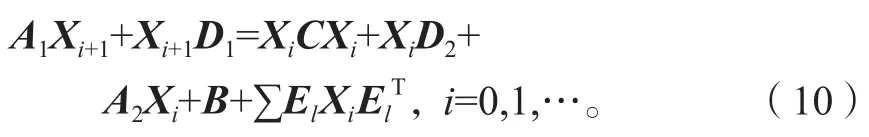
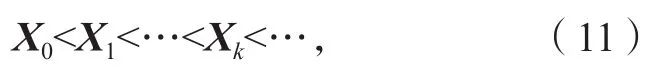
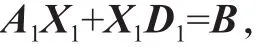
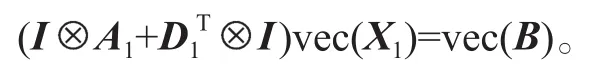
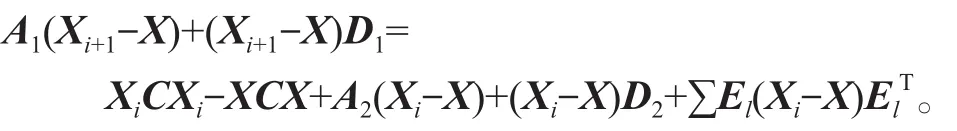
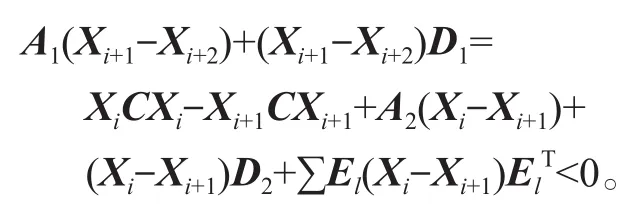
4 数值实验
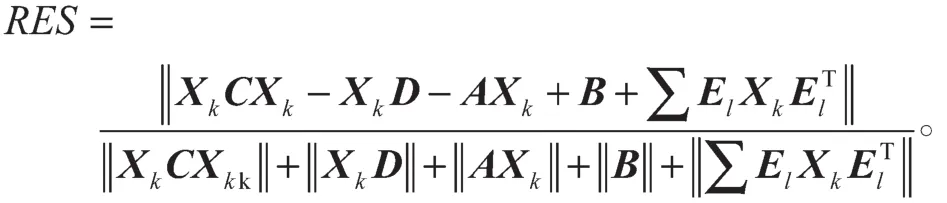




5 结语

