轴力-弯矩相互作用恢复力模型开发与评估

补国斌，谭良斌，宾 佳

（1.湖南工业大学 土木工程学院，湖南 株洲 412007；2.湖南中天建设集团股份有限公司，湖南 株洲 412003）

1 研究背景

随着基于性能抗震设计理论的不断发展和完善，结构弹性与弹塑性时程分析方法在土木工程行业的实际工程和科研领域中得到了广泛应用[1]。建筑结构弹性和弹塑性动力时程分析中，结构或构件的弹塑性分析模型可以基于楼层、构件、截面和材料4个不同的层次。从楼层到材料层次，随着建模程度的逐级精细化，计算效率相应降低。其中，基于构件或截面层次的分析模型一般采用恢复力模型或称滞回模型表征力与位移的滞回关系，主要包括折线形恢复力模型和曲线型恢复力模型[2-5]。但是，这些模型大多为平面恢复力模型，考虑多轴加载条件下变轴力-双向弯矩相互作用的模型相对较少[6]。

考虑变轴力对弯矩的影响以及双向弯矩的相互耦合作用，一直是基于截面层次恢复力模型的难题之一[7]。基于材料层次的单元模型，如纤维模型（fiber model）和多弹簧模型（MS model），虽然均能自动考虑变轴力与双向弯矩的耦合作用[8]，但是它们对于庞大的高层和复杂结构而言，其计算效率较基于构件或截面层次的恢复力模型有较大程度的降低。并且因为钢筋混凝土结构力学机理和变形性能的复杂性，有时候基于构件试验拟合的构件或截面模型反而能够更好地反映一些特殊复杂的结构受力行为[9]。中国《建筑抗震设计规范》2016版（GB50011—2016）明确指出：对复杂建筑结构进行多遇地震作用分析时，应该采用不少于两个合适的力学模型进行分析和比较[10]。因此，开发具有足够的精度、基于截面层次的变轴力-双向弯矩相互作用模型，不仅能够提高计算的效率，而且对建筑结构的弹塑性分析具有现实意义。

本文拟针对以上制约结构弹塑性分析技术发展的关键问题，开发轴力-弯矩相互作用恢复力模型（简称N-M模型），并介绍其开发的基本思路和原理。最后，以一具有实测震害记录（加速度、速度和位移）的框架结构模型为对象，并与基于纤维模型（Fiber模型）的计算结果进行对比，综合评估N-M模型在模拟结构非线性动力响应、开展振型分析和预测结构整体极值响应中的有效性。

2 轴力-弯矩相互作用模型开发原理

采用C++语言，基于金属塑性理论（metal plastic theory），开发了轴力-弯矩相互作用模型，简称N-M模型。通过轴力-弯矩相互作用屈服线（N-M曲线）表征轴力和单向弯矩之间的相互作用，如图1所示。图1中N和M分别为构件的轴力和弯矩，C和T分别表示受压和受拉状态，下标c和y分别表示开裂和屈服状态。B和B′代表大小偏心情况的界限受力状态，Mm和Mm′表示开裂线与屈服线交点对应的弯矩。开裂线假定为直线，可通过弯矩为0

的点和开裂弯矩对应点两点确定。屈服线可以假定为直线、多折线或抛物线形式，图中右半部分和左半部分分别代表正负弯矩情况。可通过各种截面分析工具或规范公式确定特征点，再作出曲线[11]。

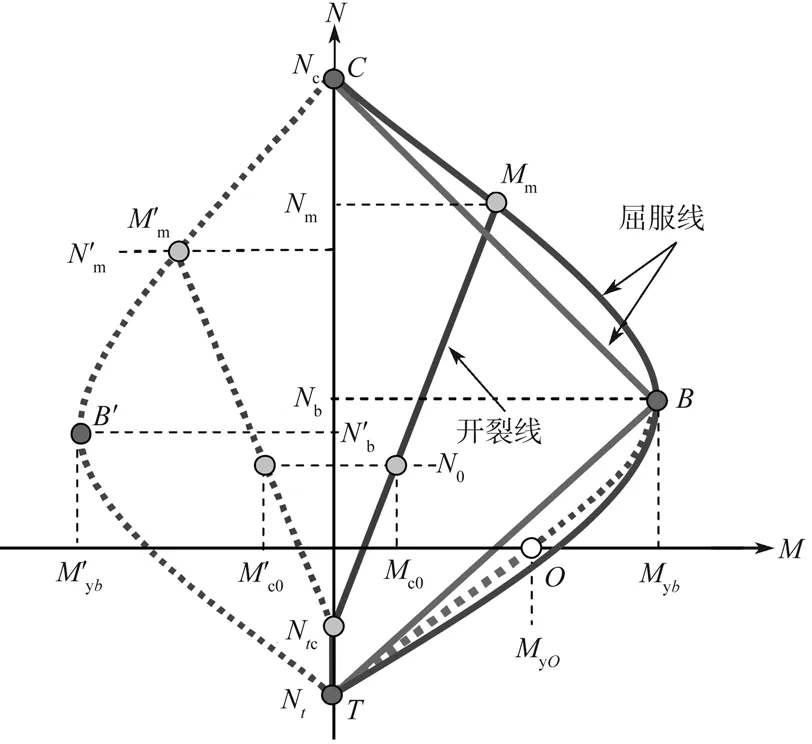
图1 轴力-弯矩相互作用曲线Fig.1 Axial force-bending moment interaction curves

采用双轴弯矩屈服线（M-M曲线）表征双向弯矩的耦合关系，如图2所示。图2中，x和y表示加载的方向；p代表屈服或极限状态；r表示转角；ρ和ρ′分别表示前加载向量和后加载向量；Δρ表示位移增量向量。

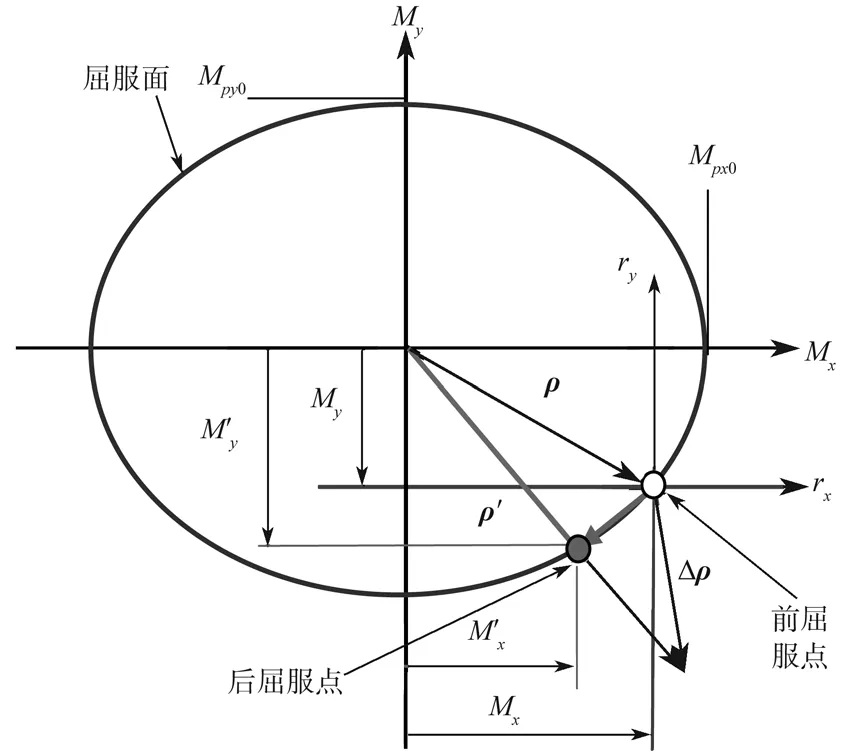
图2 双轴弯矩相互作用曲线Fig.2 Bi-axial bending moment interaction curves

目前，N-M模型的源代码已被添加进结构静动力非线性分析程序CANNY[12]，程序基于试验对比结果给定了默认的模型参数，以便于科研或者工程应用。关于该模型更详细的原理可以参考CANNY程序说明手册。

3 结构模型、地震动输入和评估方法

3.1 结构模型

本研究采用美国 CSMIP（California Strong Motion Instrumentation Program）强震记录数据库[13]提供的有实测震害记录的建筑，对N-M模型进行评估。该建筑建于1966年，为钢筋混凝土框架结构，其平面和立面示意及1994年Northridge地震中加速度测点布置如图3所示，图中除截面尺寸单位为英寸外，其余单位均为mm。其中，Ch.1～Ch.16表示楼层不同位置处测点，各测点的加速度、速度和位移时程见文献[14]。该建筑先后经历了1971年San Fernaddo地震、1987年Whittier地震和1994年Northridge地震。在前两次地震中，该建筑发生了轻微的损伤，并且进行了一定程度的加固修复。在1994年Northridge地震中，发生了较为严重的破坏，各柱出现了不同程度的剪切破坏（见图4）。

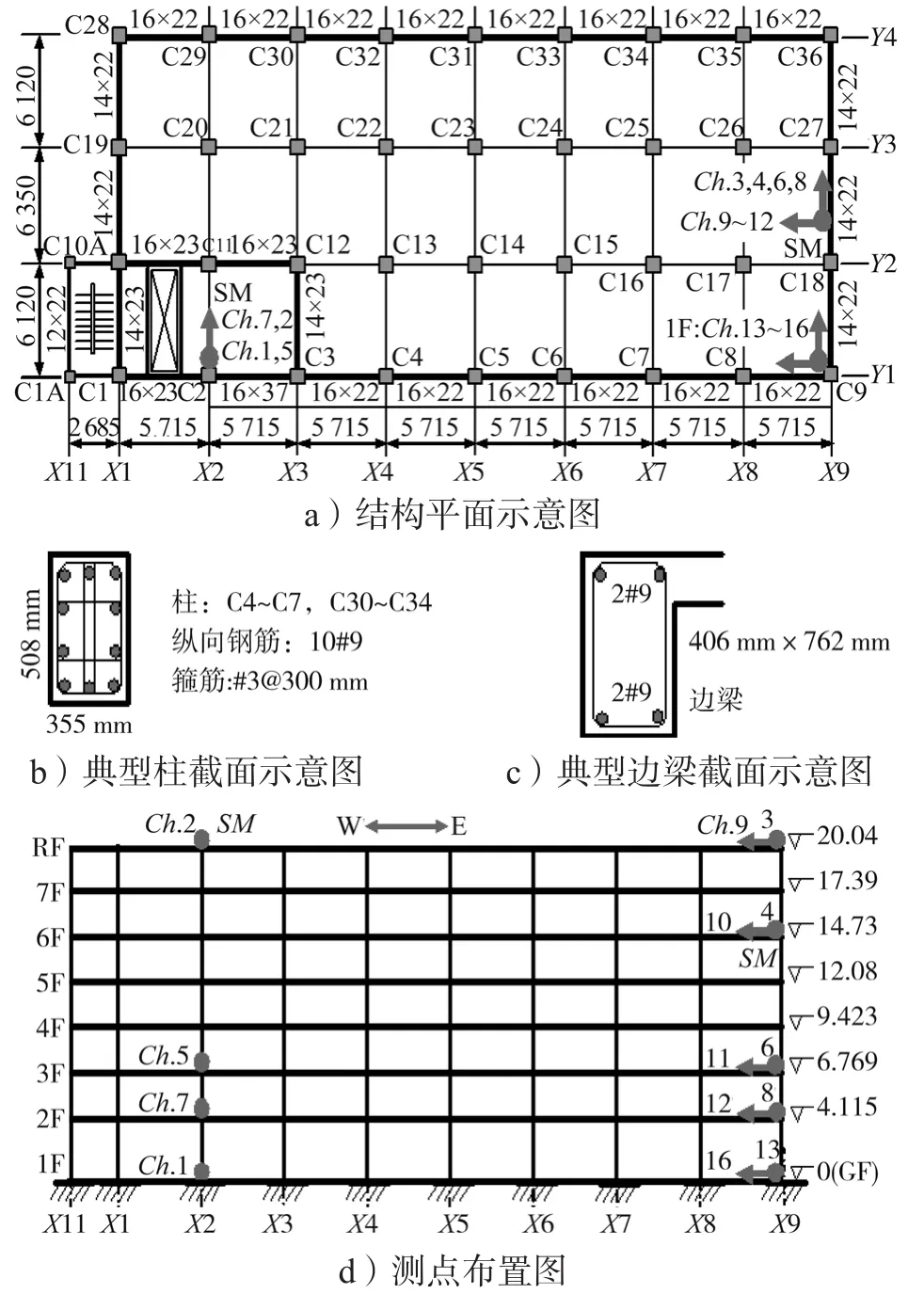
图3 结构平立面及加速度测点布置Fig.3 Layout of structural plan,elevation and acceleration measuring points

图4 柱剪切破坏Fig.4 Shear failure of columns

该结构模型的详细信息，如材料、荷载、设计条件和配筋等信息，见文献[14]。

3.2 地震动输入

地震动输入如图5所示。其中TX、TY、TZ和RZ分别为x，y，z平动方向和绕z轴转动方向。采用加速度时程输入方式，对应的加速度测点编号见图5。

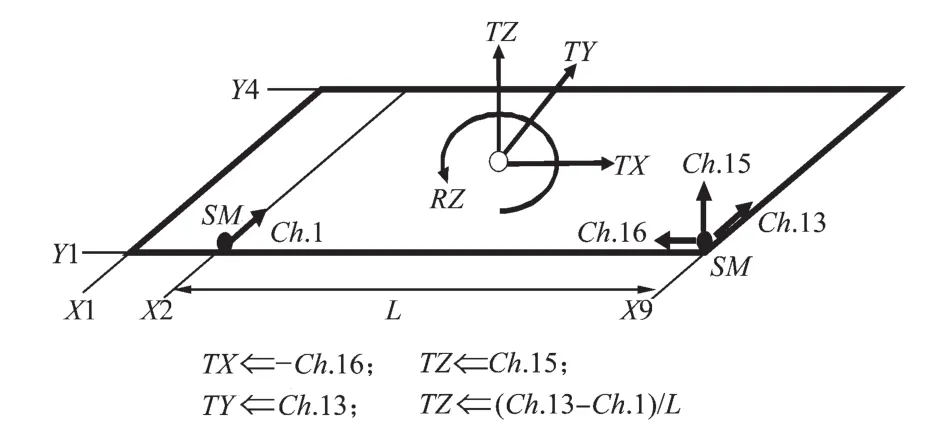
图5 地震动输入Fig.5 Seismic input

3.3 评估方法

基于前文论述的N-M模型和地震动记录，采用CANNY程序建立3.1节中所示的结构模型，并且进行动力非线性时程分析，同时也进行低周反复荷载作用分析。将时程分析结果与震害记录进行对比，以评估N-M模型模拟结构动力响应的有效性。对于振型分析和整体极值响应数据，因为震害记录中未提供或者记录不全面，故采用基于N-M模型的结果和当前广泛应用并且精度较高的纤维模型计算结果进行对比分析。

4 轴力-弯矩相互作用模型的评估

4.1 时程分析结果与震害记录对比

图6和图7分别为N-M模型工况与实测记录下顶层x方向和y方向的加速度、速度和位移时程的记录结果。

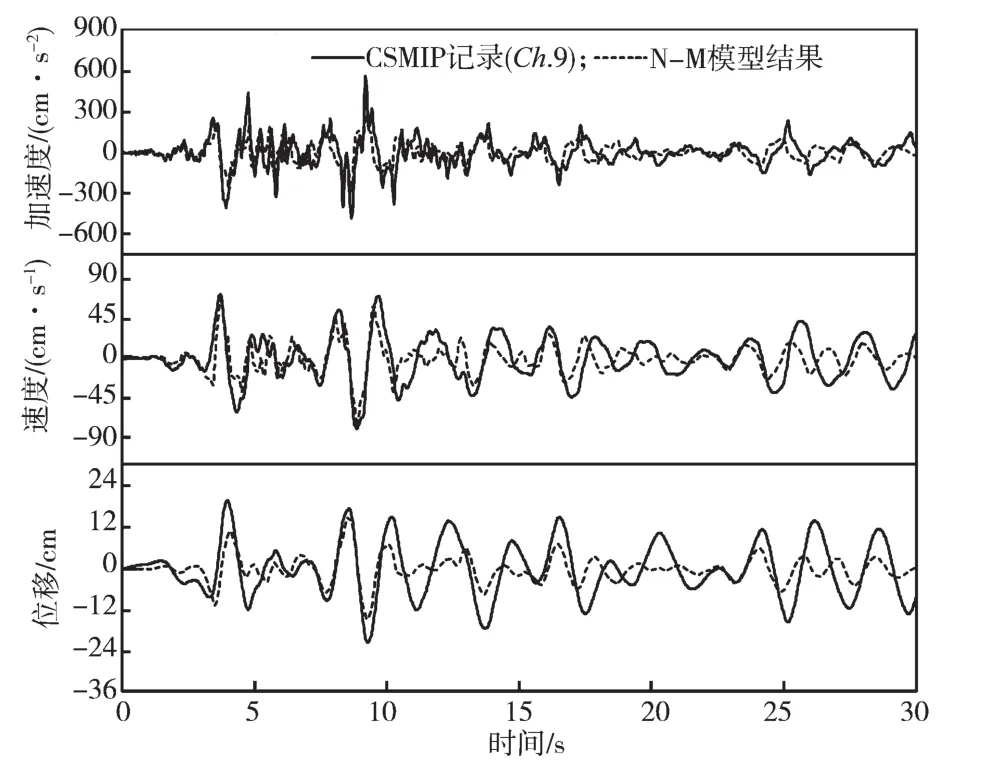
图6 顶层x方向时程对比曲线Fig.6 Time history comparison curves of roof in x direction

由图6可以得知，顶层x方向的加速度、速度和位移时程数值结果与实测记录数据具有良好的吻合度，且加速度时程曲线的吻合度最高。x方向的顶层位移时程与实测记录有些许差距，可能的原因是该建筑结构先后经历了1971年的San Fernaddo地震和1987年的Whittier地震，有轻微的累积损伤，而分析中并没有考虑这两次地震的影响。且结构在前两次地震损伤后进行了一定程度的加固，本次模拟中因无法准确估量故也未考虑加固的影响。

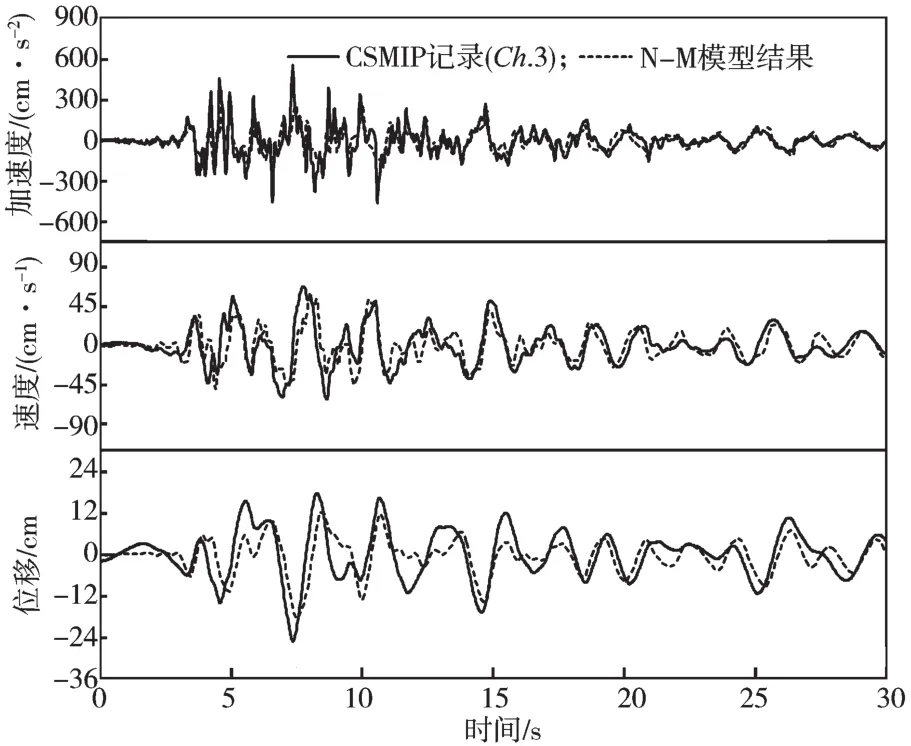
图7 顶层y方向时程对比曲线Fig.7 Time history comparison curves of the roof in y direction

由图7可以得知，顶层y方向的加速度、速度和位移时程数值结果与实测记录数据同样具有良好的吻合度，且加速度时程曲线的吻合度最高。对比图6和图7中的相应曲线可以得知，y方向的时程曲线吻合度相对于x方向的更优。因地震工程的复杂性，从土木工程应用的角度，可以确定图6和图7已经达到高度吻合的水平。

4.2 振型分析结果

因CSMIP没有提供结构的周期和频率等振型数据，故采用目前广泛应用且精度较高的纤维模型（Fiber模型）对3.1节所述结构建立数值模型。所得N-M模型和Fiber模型工况的振型分析数据如表1所示。表中，T表示结构的周期，相对误差以纤维模型为判定基准。

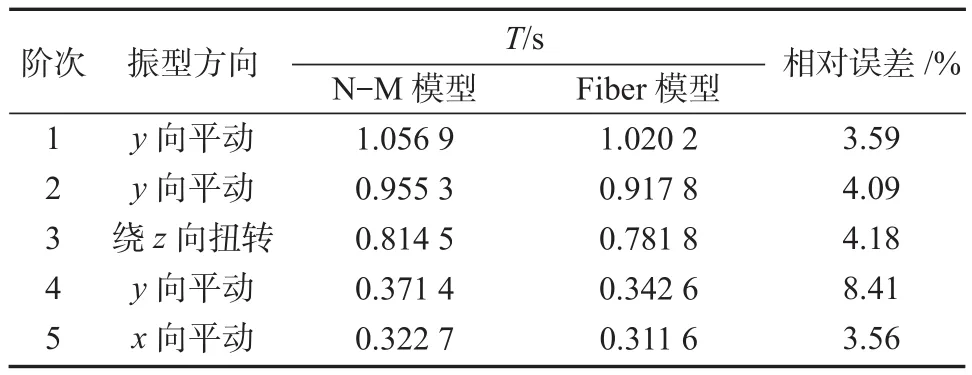
表1 振型分析结果对比Table1 Comparison of modal analysis results

由表1可知，N-M模型工况和Fiber模型工况下结构的振型方向完全一致，振型结果非常接近，最大相对误差不超过10%。因而，N-M模型在振型分析中具有较高的精度。

4.3 结构整体响应极值

因部分楼层未布置加速度测点或测点破坏，无法对各楼层响应极值进行全面对比，故采用Fiber模型工况与N-M模型工况进行对比。图8所示为两种模型工况下最大层间剪力的结果比较。

图8 两模型的最大层间剪力比较Fig.8 Comparison of maximum inter-story shear forces between the two models

由图8可以得知，两模型工况下各层x向和y向的最大层间剪力均较为接近，最大相对误差分别为8.0%（x方向，第7层）和5.5%（y方向，第7层），均未超过10%，表明N-M模型具有较高精度。

图9所示为两种模型工况下最大层间位移角的结果比较。

由图9可以得知，两模型工况下各层层间位移角均在1/50（框架结构弹塑性位移角限值）以内。且各层x方向和y方向最大层间位移角均较为接近，最大相对误差分别为7.2%（x方向，第3层）和8.9%（y方向，第4层），均未超过10%，也表明N-M模型具有较高精度。

4.4 低周反复荷载作用下力与位移的关系

分别采用N-M模型和Fiber模型，以控制顶点位移为加载准则，对模型进行低周反复荷载作用分析。加载控制的位移分别为0.1,-0.1,0.2,-0.2,0.3,-0.3,0.4,-0.4,0 m，每步位移增量为0.002 m。图10所示为低周反复荷载作用下两模型4～5层层间剪力和层间位移关系对比（即仅取中部楼层作为代表楼层进行比较）。

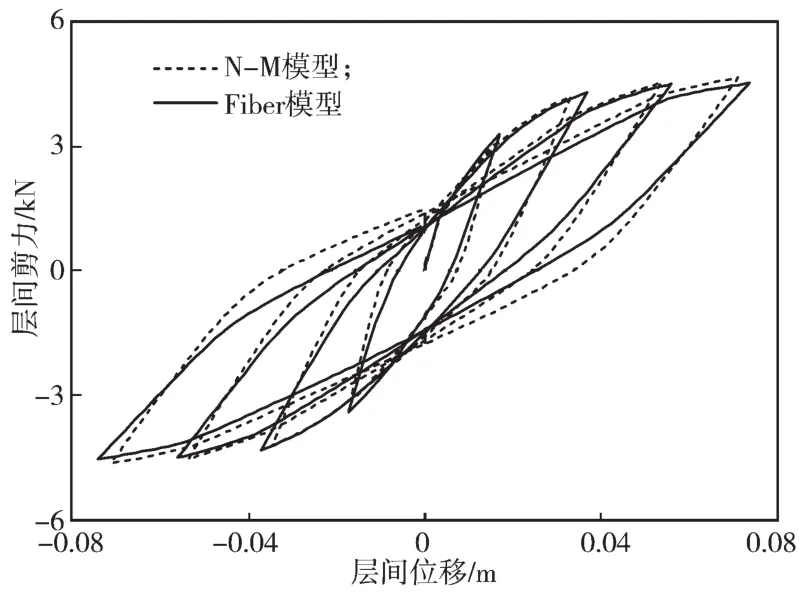
图10 两模型的力与位移关系比较Fig.10 Comparison of force-displacement relationbetween the two models

由图10可以得知，两模型的层间剪力和层间位移关系总体吻合良好。两者骨架曲线和加卸载刚度基本一致，但是N-M模型的峰值点数值略小于Fiber模型的对应值。Fiber模型模拟的捏缩滑移效应比N-M模型的模拟效果略微明显。

5 结论

本文研发了轴力-弯矩相互作用恢复力模型（N-M模型），介绍了其基本原理，并采用有实际震害记录的框架模型进行模型的可靠性评估，可得出如下结论：

1）研发的N-M模型采用C++语言编程，基于金属塑性原理，可通过轴力-弯矩相互作用曲线表达轴力和单向弯矩的相互作用，采用双轴弯矩屈服线表达双向弯矩的耦合影响。

2）N-M模型在预测和模拟结构动力非线性时程反应（加速度、速度和位移等）、振型分析和动力响应极值和低周反复荷载作用下的响应方面，均具有较高的可靠度，与实测震害记录或成熟的纤维模型计算结果相比，相对误差均在10%以内。

3）N-M模型相对于纤维模型，具有力学机理更明确、编程实现更简单、计算更可靠、计算效率更高等优点，可在结构非线性分析中进一步完善和加以推广应用。