筏板基础刚度取值对其承载性状影响的数值分析

， ，，

（湖南工业大学 土木工程学院，湖南 株洲 412007）

1 研究背景

随着我国经济的持续、快速发展，城市建设和相应的基础设施建设取得了快速发展。在多高层建筑物施工过程中，并不是所有的地基承载力都符合要求，所以如何减小对地基土的附加压力就显得格外重要，筏板基础就是这种情况下的产物。

筏板基础不仅能满足地基土的承载力要求，而且可以依靠基础的连续性和双向抗弯性能来加强建筑物的抗弯刚度，对地基的不均匀沉降具有很好的调整能力。而且它施工简单，工期相对较短，具有良好的经济性及实用性。

许多学者通过数值模拟、实际工程等方式对筏板基础进行了相关研究[1-6]。如孙衍法等[7]通过有限元模型，对已有各种简化模型进行了分析比较，得出各种简化模型的优缺点，并且通过比较筏板基础厚度、地基土的刚度等因素对筏板受力机理的影响，得到筏板基础优化设计的依据。吴春萍等[8]通过有限元数值模拟，研究了筏板基础边缘外伸长度对平板式筏板基础沉降问题的影响程度，得知外伸长度对基础沉降具有一定的影响，但是外伸长度过大或者过小对沉降均不利。孙秀竹等[9]利用ANSYS软件建立了地基与基础的整体模型，两者之间通过接触面连接，并且分析了筏板基础刚度对基底反力和上部结构内力的影响，所得结果表明，对于减小基础沉降和减小在上部结构中产生的次应力，筏板基础存在一个合理的厚度。宫剑飞等[10]通过对实际工程的沉降观测，认为大面积筏板基础的沉降有别于传统的高层建筑物以下的基础沉降，其认为筏板基础在考虑是局部弯曲还是整体弯曲时，可以用抗裂度进行衡量。

还有学者通过对桩筏基础中的筏板基础进行研究，如王杰等[11]通过有限元法建立了桩筏、地基土、上部结构的共同作用分析模型，研究了筏板厚度对桩顶反力、最大挠度、筏板内力的影响，得知设计中存在一个最佳筏板厚度值。陈云敏等[12]提出一种新的桩筏基础相对刚度的表达式，并从桩反力的角度出发，得到了合理板厚的表达式。

目前，有关筏板基础的数值模拟试验研究中，有的研究只考虑将筏板基础看做一块板进行受荷载分析，而没有考虑地基与基础之间的相互作用；有的研究只是通过建立筏板基础与土体的接触面，却并没有考虑四周土体对筏板基础的包裹作用；还有的研究仅通过建立统一的桩筏基础模型来分析筏板基础的受力特性。但是在实际工程中，筏板基础单独受荷（即底部没有桩）的情况也是存在的。而在筏板基础的相关研究中，刚度对筏板基础的影响分析相对较少，有的也只是单纯考虑筏板基础刚度在不同取值情况下的承载性状变化，并没有把土体与筏板基础相互作用这一必然因素考虑进去。

基于已有研究，本文拟利用FLAC3D有限差分软件能够考虑土体与基础的相互作用的特点，分析不同刚度的筏板基础在土体中承载性状的差异性，以期为类似工程提供一定的理论参考。

2 数值模拟

2.1 模型建立

由于本文主要针对基础刚度对筏板基础承载性状的影响展开相关研究，故忽略上部结构刚度的影响，直接利用FLAC3D软件建立地基与土体相互作用的数值模型。为了使建立的模型能够简单真实地反映地基与筏板基础相互作用的影响，在地基与土体之间建立接触面，筏板基础相对于周围土体材料而言是刚性的，采用“硬”接触描述两者之间的真实接触面，接触面相关参数见表1。

表1 接触面参数Table1 Parameters of the contact surface

初步选取筏板厚度为0.8 m，埋深为1.5 m，筏板的基础模型尺寸如图1所示。模型分为两层土体，便于直观地反应筏板基础的变形情况。为了消除基础沉降对周围土体的影响，结合前人的研究[9]，土体深度取筏板底部以下50 m，水平方向自筏板边缘外取32 m，其计算模型如图2所示。

图1 筏板基础截面示意图Fig.1 Schematic diagram of raft foundation section

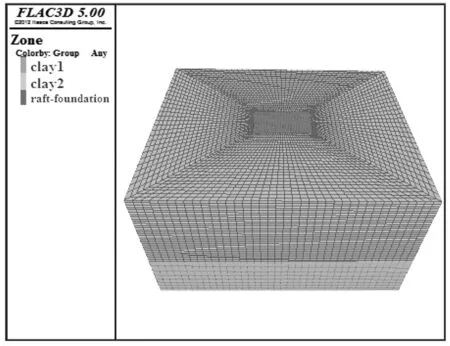
图2 筏板计算模型图Fig.2 Calculation model

2.2 本构模型与边界条件

筏板基础宜采用各向同性弹性本构模型，筏板基础长 19.2 m、宽 13.2 m，密度为2 500 kg/m3，泊松比取0.23，荷载间距为6 m，荷载距筏板边缘0.6 m，初步取筏板基础弹性模量为8 GPa，土体采用典型的摩尔-库伦弹塑性本构模型，土层分布及相关物理参数如表2所示。本模型的边界条件如下：固定模型底部各个方向的位移，四周约束水平位移，顶面为自由边界，不进行固定；应力边界条件为只考虑筏板基础和土体在Z方向的自重应力，忽略水压力以及其它外加荷载的影响。

表2 土层物理参数Table2 Physical parameters of soil layers

2.3 加载

首先，需要对计算模型进行自重应力平衡处理，然后对筏板基础施加外荷载。筏板基础上所受集中荷载的大小如图1所示。考虑到基础受荷载作用的面积为0.6 m×0.6 m，数值计算时柱轴力以均布荷载的形式施加到柱子所在的范围。

3 数值模型验证与分析

将FLAC3D数值模拟筏板基础的三维变形云图放大200倍后，如图3所示。

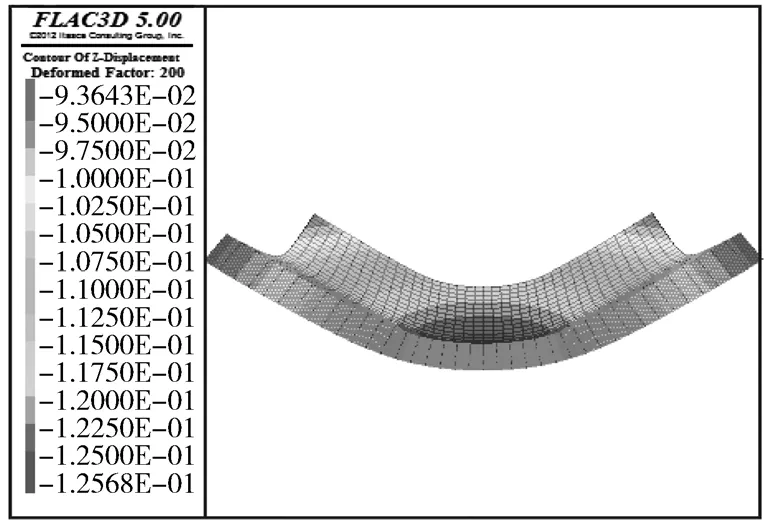
图3 筏板基础三维变形图Fig.3 Three-dimensional deformation diagram of raft foundation

由图3可以看出，筏板基础沉降的最大值发生在基础的中间部位，此次数值计算所得的结果与中国科学建筑研究院所做的试验得出的沉降等值线图形状基本一致[10]，说明本文所建立的数值模型是合理的。

对筏板基础B轴进行位移沉降监测，得到的沉降位移曲线如图4所示。

图4 B轴沉降监测曲线Fig.4 B-axis settlement monitoring curve

由图4可以看出，沉降曲线呈抛物线，由曲线可知，基础最大沉降量出现在B轴中点附近，与文献[4]所得的结果基本一致。

4 数值分析结果

4.1 基础刚度的影响

数值模拟中，通过改变筏板基础刚度的取值，对基础的承载性状进行系统研究，各试验相应的刚度取值如表3所示。

表3 筏板基础刚度取值Table3 Stiffness values of raft foundation

4.1.1 基础刚度对筏板基础内力的影响

图5所示为筏板最大竖向应力随基础刚度的变化曲线。

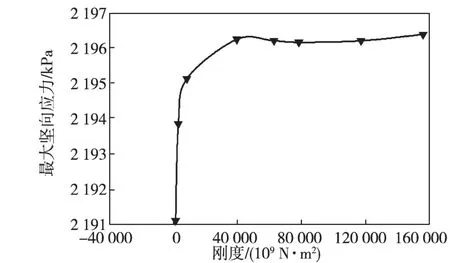
图5 筏板的最大竖向应力变化曲线Fig.5 Maximum vertical stress variation curve

由图5所示最大竖向应力变化曲线可以得知，当筏板刚度EI为622.85×109～7 785.67×109N·m2时，筏板的最大竖向应力的增速特别快；当刚度EI为7 785.67×109～ 38 928.38×109N·m2时，筏板的最大竖向应力增速逐渐变缓；当刚度EI为38 928.38×109～155 713.54×109N·m2时，筏板基础的最大竖向应力基本不变，趋于一个定值。或者说，在综合考虑筏板基础自身的因素下，考虑其经济效益，基础的最佳刚度为77 850.68×109N·m2左右。如果此时进一步增加基础刚度，其对应力分配的调整效果已不再明显。

图6是荷载作用在不同刚度的筏板基础下的相应应力云图。

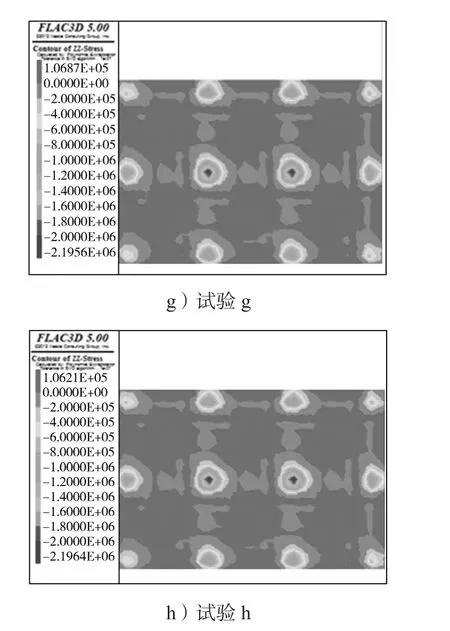
图6 筏板基础应力云图Fig.6 Stress nephogram of raft foundation

由图6可以得知，筏板基础的最大的竖向应力发生在中间桩的位置处，而4个角上受到的竖向应力值相对最小。

4.1.2 刚度对筏板基础最大沉降量的影响

图7所示是荷载作用在不同刚度的筏板基础下产生的相应沉降云图。

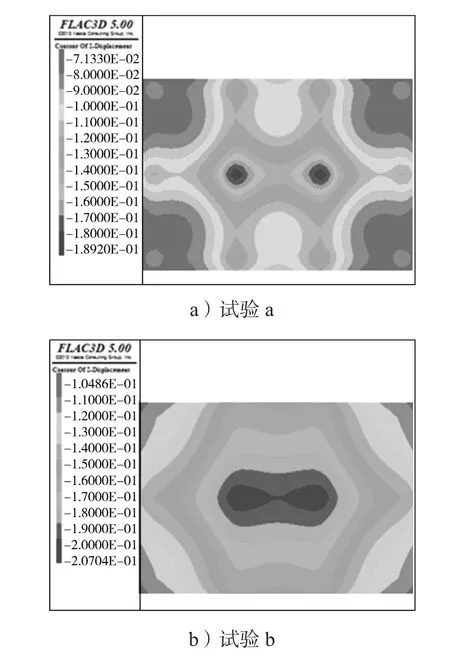
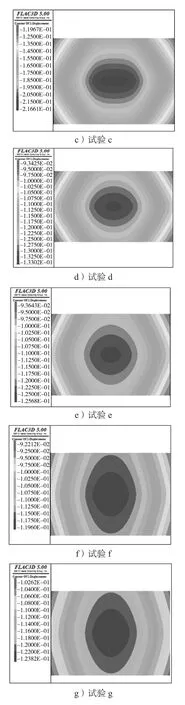
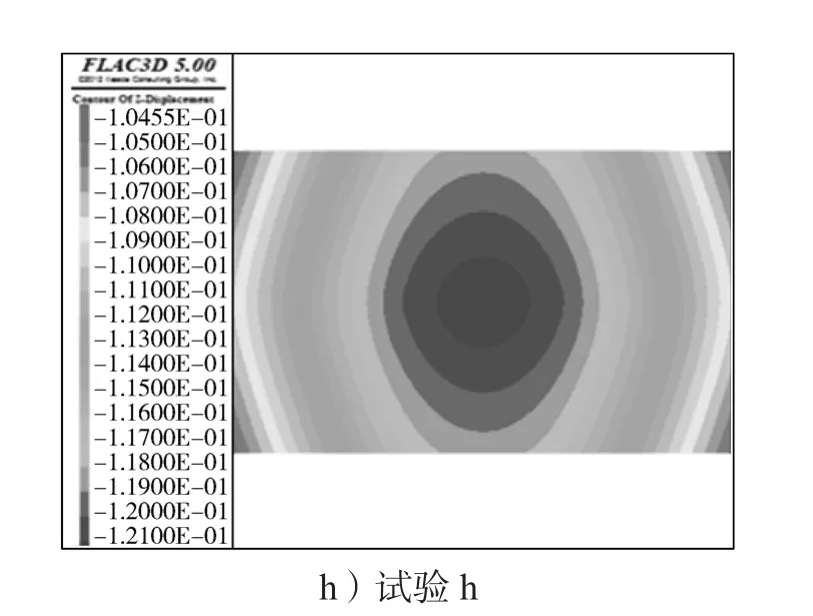
图7 筏板基础沉降云图Fig.7 Nephogram of raft foundation settlement

对位移云图进行分析，由图7中的a、b图可知，此时刚度相对较小，筏板基础产生较为严重的局部变形，调整不均匀沉降的能力很弱，局部的基础不能把荷载有效地分配给筏板基础的其他部分，导致其产生了局部的沉降异常。随着刚度的增加，最大沉降量越来越小，且沉降云图变化越来越规则。由图a筏板基础的中点附近出现局部沉降反常，基础的翘曲程度极为严重，再到图g中的最大沉降值范围变化越来越大，其范围逐渐往四周扩散，沉降云图中不再出现如图a的奇异区域，说明筏板基础的整体沉降越来越均匀，表明随着筏板基础刚度的增加，其抗弯能力随之增加，其整体的弯曲程度变得越来越缓和，这对消除基础不均匀沉降是有利的。

由图7可以推断，筏板基础的最大沉降出现在基础中心附近。将基础的最大沉降值与刚度关系绘成曲线，如图8所示。

图8 筏板基础最大沉降值随刚度的变化曲线Fig.8 Maximum settlement change curve of raft foundation with stiffness

由图8 可知，当刚度EI小于 7 785.67×109N·m2时，筏板基础的最大沉降值随着刚度的增加而增大，但是从曲线的大致走向来看，特别是当刚度值大小为7 785.67×109～ 77 850.68×109N·m2时，筏板基础的最大沉降值随着刚度增大而急剧减小，甚至远小于刚度等于 7 785.67×109N·m2时的值，由 0.216 61 m 减少到0.119 586 m，约减小了44.7%；当刚度值再持续增加至 155 713.54×109N·m2时，其减小的幅度接近1%，最大沉降值趋于一个定值。

4.1.3 刚度对基础沉降以及沉降差的影响

图9所示为基础沉降差随基础刚度的变化曲线，由图可以得知，筏板基础的沉降差随着刚度EI的增大而逐渐减小。当刚度值为622.85×109N·m2～38 928.38×109N·m2时，沉降差减小了 66.7%，刚度增加到 155 713.54×109N·m2时，沉降差较开始时减小了85.6%，整块筏板基础的沉降差仅为0.061 6 m。这一结果说明，刚度EI值越大，筏板基础的沉降越均匀，其翘曲的程度不再明显。

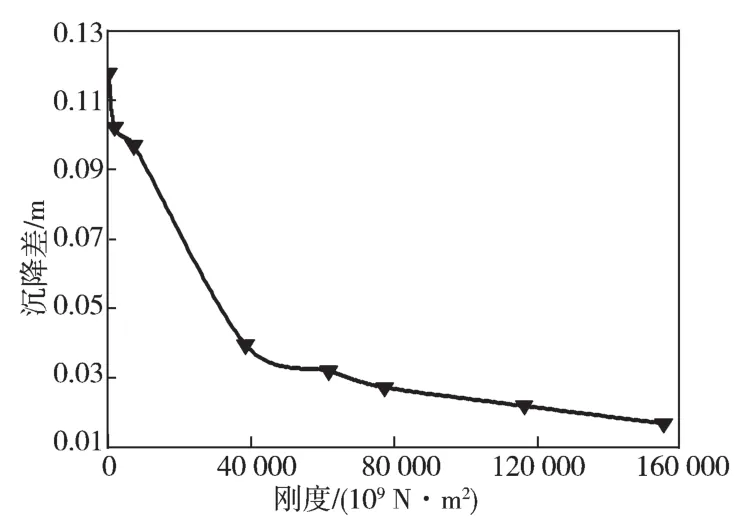
图9 筏板基础沉降差随基础刚度的变化曲线Fig.9 Curve of settlement difference of raft foundation with foundation stiffness

4.1.4 理论计算与试验结果对比

筏板基础刚度对沉降的影响实际上是层状弹性地基上筏板基础的沉降计算问题。利用层状弹性半空间体系的相关理论对筏板基础发生最大沉降的位置进行变形理论计算[13]，并与试验得到的结果进行比对，因在试验中刚度值较小时，筏板基础发生了严重的局部变形，为防止不满足小挠度问题的假设，故只取E值为8,10,15,20 GPa时的变形值与计算值进行对比，对比结果如表4所示。

表4 试验与理论计算对比Table4 Comparison between experiment and theoretical calculation m

由表4可以得知，当E值为8 GPa和10 GPa时，两者的计算误差分别约为12%和4%，但是当E值为15 GPa时，误差达到了48%左右，考虑层状弹性地基得到的筏板基础沉降值与本次试验得到的沉降值相差较大，故在筏板基础设计时，不考虑地基的分层计算基础沉降是不可取的。但随着刚度的变化，最大沉降值的变化趋势基本上是一致的。

4.2 群柱效应的影响

柱荷载传递到筏板基础上的力简化成独立模式与考虑上部结构影响的群柱效应存在一定的区别。建立考虑群柱效应的数值模型，如图10所示，将其试验结果与本文不考虑群柱效应得到的试验结果进行对比分析。

图10 考虑群柱效应的模型示意图Fig.10 Schematic diagram of the model with group column effect considered

为保证两种情况下筏板基础所受荷载相同，在对群柱施加荷载时要考虑柱体自重，即施加在柱体上的荷载要减去柱体的自重。

4.2.1 群柱效应对筏板基础最大竖向应力的影响

图11是考虑群柱效应和无群柱效应时筏板基础的最大竖向应力值变化曲线对比图。

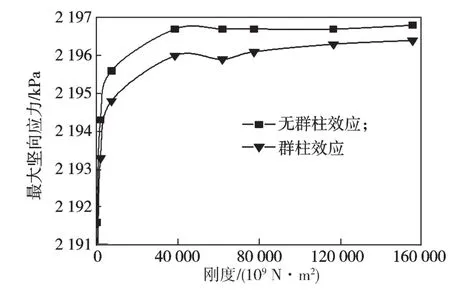
图11 筏板基础最大竖向应力值对比图Fig.11 Comparison diagram of maximum vertical stress values of raft foundation

由图11可知，从应力变化趋势上分析，无论是否考虑群柱效应，筏板基础的最大竖向应力值在筏板基础刚度值达到 38 928.38×109N·m2后基本保持不变。群柱效应的存在对最大竖向应力值有一定的影响。在刚度较小时，群柱效应对最大竖向应力值的影响不明显，两种情况下的最大竖向应力曲线几乎是重合的。当刚度值超过 7 785.67×109N·m2时，考虑群柱效应的筏板基础的最大竖向应力值小于无群柱效应时的应力值，两者最大时相差了0.03%。群柱效应对于筏板基础的最大竖向应力有一定的影响，但这种影响只有刚度达到一定值后才会显现出来，并且这种影响很小。

4.2.2 群柱效应对筏板基础最大沉降量的影响

图12是考虑群柱效应和无群柱效应时筏板基础的最大沉降值变化曲线对比图。

图12 筏板基础最大沉降值对比图Fig.12 Comparison diagram of maximum settlement value of raft foundation

由图12可以得知，在两种情形下，筏板基础最大沉降值的变化趋势几乎是相同的。但是考虑了上部结构群柱效应影响的筏板基础的最大沉降值明显低于将柱荷载简化为独立模式作用于筏板基础情形下的最大沉降值，两者的差值最大时约相差了31%。可见，考虑群柱效应影响时，筏板基础的最大沉降值将会减小；而不考虑群柱效应的影响将会高估筏板基础的沉降量。

5 结论

通过数值计算的方法，分析了筏板基础刚度的变化对最大竖向应力、最大沉降值、沉降差等的影响规律，可得出如下结论：

1）增大筏板基础的刚度的确可以有效减小筏板基础的最大沉降量和沉降差，特别是对于减小沉降差而言，刚度越大越有利。

2）实际工程中刚度并不能无限增大，设计时应该综合考虑其变形、受力，以及经济合理性，因为当筏板基础的刚度达到一定值后，对减小其最大沉降量已无多大作用。

3）在本次试验中，最佳的刚度值为10 GPa。这样既可保证筏板基础相对均匀沉降，又能达到规范要求的最大沉降值，还可让其最大应力处于一个稳定的状态而不至于存在过大的应力突变，避免对结构物的不利影响。

4）柱荷载传递到筏板基础上的力简化成独立模式与考虑上部结构影响的群柱效应存在一定的区别。在本次试验中，群柱效应的存在对筏板基础最大竖向应力的影响是很小的，但对筏板基础最大沉降值的影响非常明显；如不考虑群柱效应的影响，将会高估筏板基础的最大沉降量。