一种锥形磁极电磁铁设计及吸力特性研究
张华伟,米永存,李 鹏,魏 彬,曹 宽
(西安航天精密机电研究所,西安710000)
0 引 言
电磁铁因结构简单、可靠性高、体积小等优点,广泛应用于运载火箭、导弹和雷达战车等动力系统中,用作其自动化装置中的驱动或执行元件。本文电磁铁用于失电制动执行机构中,通过电磁吸力控制机构的活动部件解锁,实现电信号对机构机械运动状态的控制。
近年来,国内外许多学者对电磁铁的性能特性作了研究。太原理工大学的王旭平等对电磁铁的磁链和动铁心位置的关系进行了分析[1]。西北工业大学的梅亮等对圆环形电磁铁进行了性能研究[2]。太原理工大学的吴波等对电磁铁进行静瞬态电磁场的仿真[3]。青岛大学的王新亮等用有限元法对电磁铁进行不同气隙下的吸力仿真,但未对优化设计进行研究[4]。So-NamYun等优化计算了电磁铁极靴参数,并通过相关实验进行了验证[5]。综上文献,主要从电磁铁的电磁和结构的角度进行研究,但对锥面吸力电磁铁有效工作特性的优化设计很少涉及。
本文以一台吸力不小于50 N的锥形磁极电磁铁样机为例,在有限的结构尺寸条件下,通过等效磁路法进行解析推导,利用解析结果进行有限元优化设计,分析了不同锥形磁极角度吸力特性的变化规律,进行了样机研制和性能对比,给出了优化结构和结论。
1 结构及工作原理
本文电磁铁是一种锥形磁极结构,其磁路主要由衔铁、端盖、机壳和磁轭四部分组成;这四部分之间的环形绝缘槽中放置电枢绕组,作为整个电磁铁的激励源,结构如图1所示。
衔铁作为整个电磁铁的活动部件,通过电信号产生电磁吸力,这就使磁化后的衔铁向磁轭运动,进而进行吸合解锁。
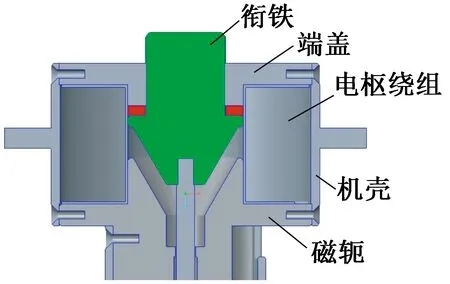
图1 电磁铁结构图
2 数学模型
目前,电磁铁性能特性求解一般采用磁路法或数值法。
2.1磁路法
磁路法是一种磁电比拟的分析方法。把电磁铁的相关磁路部件分割成各种磁阻元件,通电绕组引入磁动势等参数,组成一个磁阻电路进行求解计算。建立的磁路等效模型如图2所示。
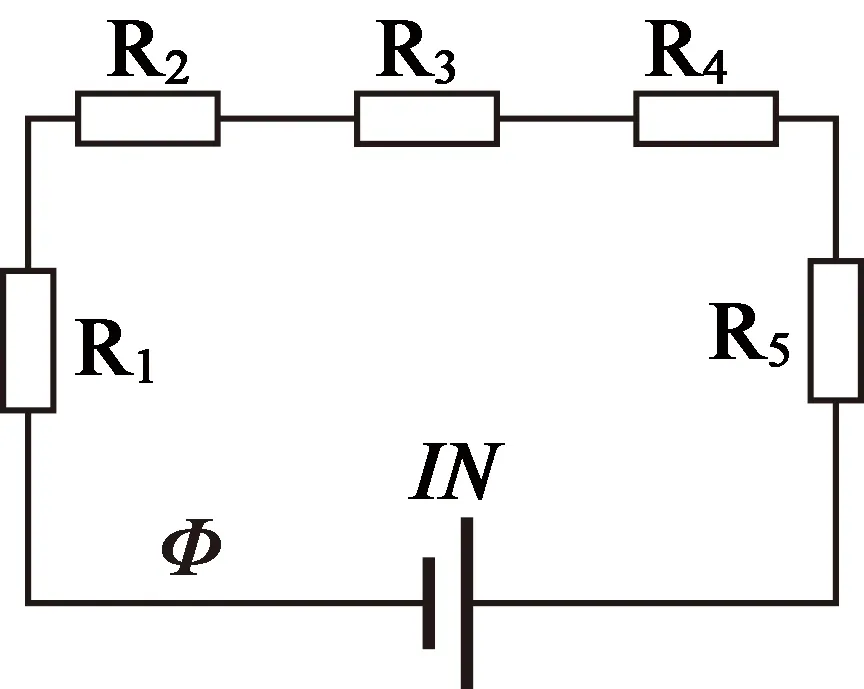
图2 磁路等效模型
图1中,R1为气隙磁阻;R2为衔铁磁阻;R3为端盖磁阻;R4为机壳磁阻;R5为磁轭磁阻;IN为磁动势。等效磁路模型需做出如下假设:不考虑漏磁影响;机壳、端盖、磁轭和衔铁以外的结构按空气磁导率建模。
根据磁路结构模型和等效磁路欧姆定律,电磁铁产生的磁动势:
IN=Φ(R1+R2+R3+R4+R5)
(1)
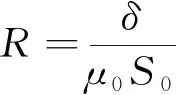
(2)
式中:μ0为空气磁导系数,μ0=1.25×10-8H/m;S0为气隙截面积(m2);δ为气隙长度(m)。
电磁吸力与气隙中磁通密度的平方及磁力线穿过磁极的总面积成正比。假设磁通密度均匀分布磁极表面,电磁吸力可表示:

(3)
式中:F为电磁吸力(J/cm);S为磁极表面积(cm2);B为磁通密度(Wb/cm)。
磁力线是封闭的曲线,满足磁路基尔霍夫第一定律又称磁通连续定律:在磁路任意节点处,进入与离开该面的磁通代数和为零。将F的单位换成千克,B的单位换成高斯,μ0数值代入式(3),得:
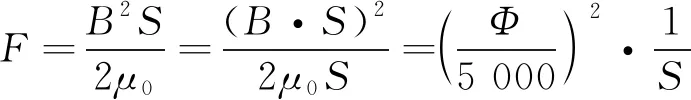
(4)
2.2数值法
数值法是通过模拟求解微积分方程,得到磁位势的分布规律,具有精确、快速等优点。静磁场分析通过麦克斯韦方程组进行微分方程求解计算:

(5)
磁性材料的磁化曲线方程有:

(6)
式中:D为电位矢量(C/m);ε为介电常数(F/m);σ为电导率(S/m);μ为磁导率(H/m)。
式(5)引入矢量磁位A,磁通密度B表示为A的旋度,即:B=×A。
把B=μH代入式(5),得:
(7)
采用圆柱坐标系分析本文的轴对称稳定磁场,式(7)写为分量形式:
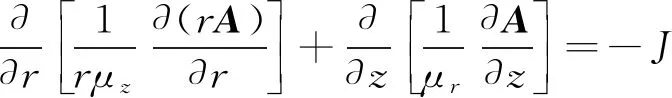
(8)
计算求解矢量磁位A,进而求出气隙磁密B,再根据式(3),得到电磁铁的电磁吸力F。
3 磁路法优选计算
本文电磁铁受结构尺寸限制,结构如图3所示。电磁铁电枢绕组最大外圆直径D1为48 mm,考虑实际绕线时的槽满率,电枢绕组外径取0.75D1,绕组内径D2为23 mm,等效外径D均为29.5 mm,电磁铁磁极端面到磁轭吸合面的距离为6 mm,电磁铁高度L为22 mm。

图3 电磁铁结构示意图
由于空气磁导率相对导磁材料磁导率要小上千倍,经基尔霍夫第二定律磁通计算,可认为磁动势主要消耗在气隙中,即:
IN=ΦR1
(9)
从图3可以看出,在保证磁轭锥口L1、磁轭锥底L2和6 mm行程不变的条件下,随着锥形磁极角度θ的增大,磁极气隙X在不断减小(磁阻随之减小)。由式(1)和式(3)可知,假设磁动势IN不变,磁极有效面积S不变(竖直方向),随着锥形磁极角度的增加,磁阻减小,磁通密度B随之变大,电磁吸力F也增大。在θ=0时磁阻最大,磁场吸力相对较小,可以以此状态为优选方案。
当θ=0时,锥形磁极面积:
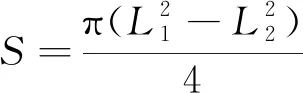
(10)
将F的单位换成牛顿,式(2)、式(4)、式(10)代入式(9),可得计算公式:

(11)
式中:g为重力加速度(m/s2)。
本文电磁铁要达到50 N的初始吸力,根据式(11)可得电动势IN=2 780.9 At。
铜线的电阻率会受工作温度的影响。因为本文设计的锥形磁极电磁铁通电时间很短,电磁铁工作温度不会过高,设电磁铁最大工作温度为60 ℃,由于电磁铁最大的供电电压为28 V,则电枢绕组的线径:

(12)
(13)
根据漆包线标准规格选取线径为0.5 mm,又电枢绕组初始设计径向截面积:

(14)
实际线圈叠绕而成,可将圆铜线等效成方铜线进行匝数折算,则线圈匝数:
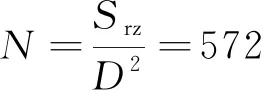
(15)
取线圈匝数为570匝,根据式(3)计算结果,要达到50 N吸力,需要的电流为4.63 A。
4 有限元优化计算
利用Ansoft软件的有限元分析计算模块,对本文优选方案进行参数化建模,并进行二维瞬态场仿真分析。设置求解边界为气球边界;线圈570 匝,激励电流4.63 A;衔铁为运动部件,额定行程6 mm。衔铁、端盖、机壳和磁轭设置为导磁材料,隔磁环、线圈骨架和电枢绕组设置为非导磁材料,其他计算区域设置为真空。电磁铁具有轴对称性,取1/2二维模型就可以计算出整个电磁铁的磁场特性,并且有利于减少计算时间,如图4所示。通过角度θ和衔铁位置的改变,计算得出不同衔铁结构和位置的电磁吸力特性曲线,如图5所示。

(a) θ=0

(b) θ=60°图4 电磁铁二维仿真模型
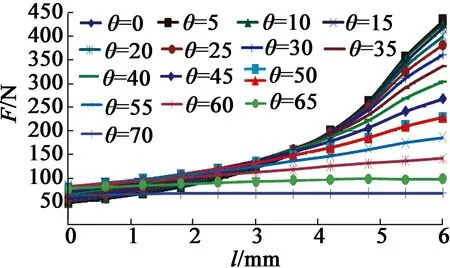
图5 电磁吸力特性曲线图
由图5可知,当θ=0时,初始电磁吸力为48.18 N,吸合时的电磁吸力为432.35 N。和本文设计值50 N相差3.6%,在工程允许的误差范围内,验证了磁极锥形角为0时,磁路法对初始电磁吸力计算的可靠性。
计算对比不同θ角度下,电磁铁吸合前的电磁初始吸力和吸合后的电磁吸力,具体参数如表1所示。
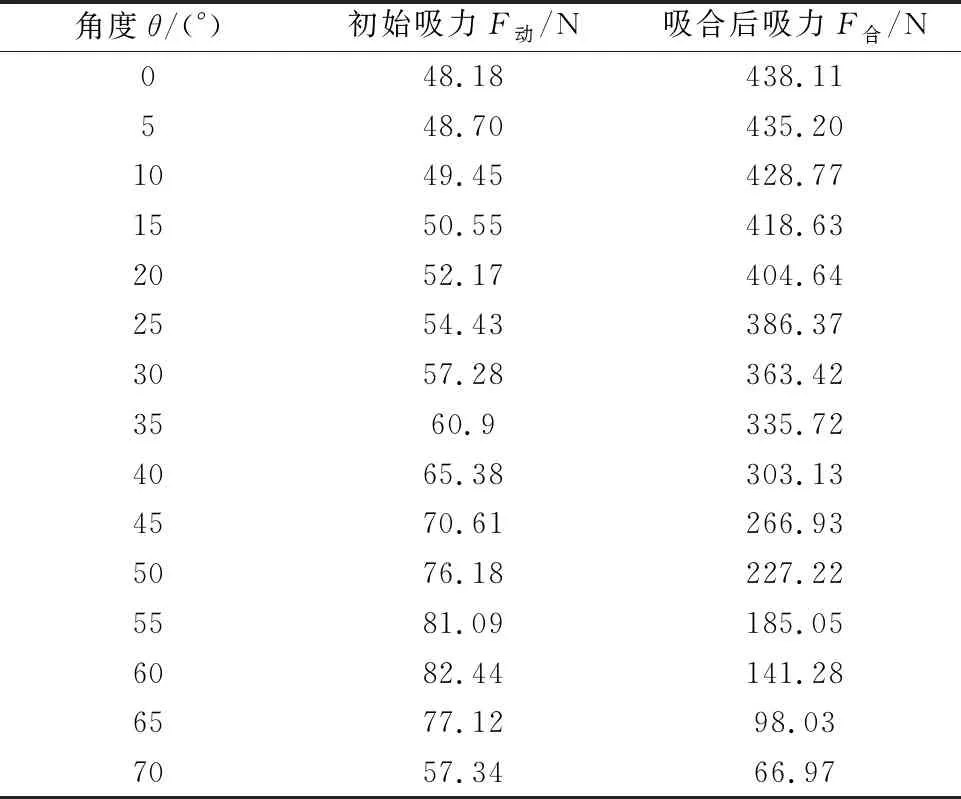
表1 不同角度θ下电磁吸力
从表1可知,随着θ角从0到70°增加的过程,初始吸力从48.18 N(θ=0)增加到82.44 N(θ=60°),然后减小到57.34 N(θ=70°),是一个抛物曲线的变化过程,在θ=60°时初始吸力达到最大值。对电磁吸力进行分析,吸力分析图如图6所示。

图6 电磁吸力分析
由图6可知关系:
F=F1cosθ
(16)
δ=6cosθ
(17)
由式(4)、式(16)和式(17)可知,当θ角增大时,气隙δ逐渐减小,电磁吸力F1在0~60°之间增加较为明显,之后增加缓慢;而轴向吸力F在60°之后开始下降,这是由于式(16)中余弦值下降幅度超过了F1的增长幅度,轴向吸力F在θ=60°达到最大值82.44 N,较48.18 N(θ=0)提高了68%,从而得到60°最优锥形磁极设计角度,电磁吸力与锥形磁极角度关系,如图7所示。

图7 电磁吸力及气隙曲线图
5 试验验证
为了验证有限元优化设计的准确性,对一台60°锥形磁极电磁铁样机进行了试验验证,如图8所示。

图8 电磁铁性能试验
本次试验额定电压28 V,对吸合电流、电磁吸力实测值与理论计算值进行了对比,如表2所示。

表2 电磁铁试验值和计算值对比
从表2中可以看出,吸合电流的试验值小于计算值,主要是由于漆包线绕制过程中,实际绕线没有很规律地绕制,造成电阻偏差。电磁铁吸力的试验值小于计算值,和试验电流偏小有很大关系。此外,仿真建模与实际机加工和装配工艺的差异也会影响测试结果。对比两种结果,误差相对较小,测试结果验证了仿真计算的可靠性。
6 结 语
本文采用磁路法和有限元计算相结合的方法,对一种锥形磁极电磁铁进行了设计和吸力特性研究,得到如下结论:
(1) 采用磁路法简化了电磁铁的等效磁路,分析了磁路磁阻,推导出锥形磁极为0时的电磁吸力特性和电磁铁各主要尺寸之间的解析式,建立了初始优选方案的数学模型,得到了有限元法的可靠验证。
(2) 利用有限元仿真计算,对不同锥形磁极角度下的电磁吸力进行优化计算,得出了60°锥形磁极的最优角度,电磁吸力较0°锥形磁极电磁铁提高了68%,为锥形磁极电磁铁的优化设计和应用提供了参考。
(3) 通过一台方案样机进行了试验验证,试验结果验证了磁路法和有限元二者相结合设计的可靠性和高效性,为同类电磁铁的设计提供了一种思路。

