新型PSGA算法在通航物流系统效能优化中的应用

张昊，安景文

(1.中国矿业大学 管理学院，北京 100083；2.中航通飞华北飞机工业有限公司，河北 石家庄 051430)

然而，遗传算法的运行性能除了与遗传算子有关，更取决于算法结构框架的效率水平.本文将尝试对遗传算法的算法结构进行重新设计，同时设计引入一种新型适应度调和因子(AF因子)，以使新算法的效率更高，更适合在通航物流系统等对算法时间效率要求较高的场景下应用.

1 PSGA改进遗传算法

1.1 基本遗传算法

遗传算法(GA)的算法流程是对自然界优胜劣汰机制的模拟与抽象，它所面向的主要应用领域是各种难以找到精确解的NP问题，主要由3种信息交换机制构成，分别是：选择算子、交叉算子与变异算子.通过建立包含多个个体的种群，对个体按照3种信息交换机制进行自身部分信息的随机互换，同时循环对种群中的个体进行优胜劣汰，使种群中个体趋于同一化，使个体的适应度值收敛，进而获得最优解.遗传算法的算法流程如图1.

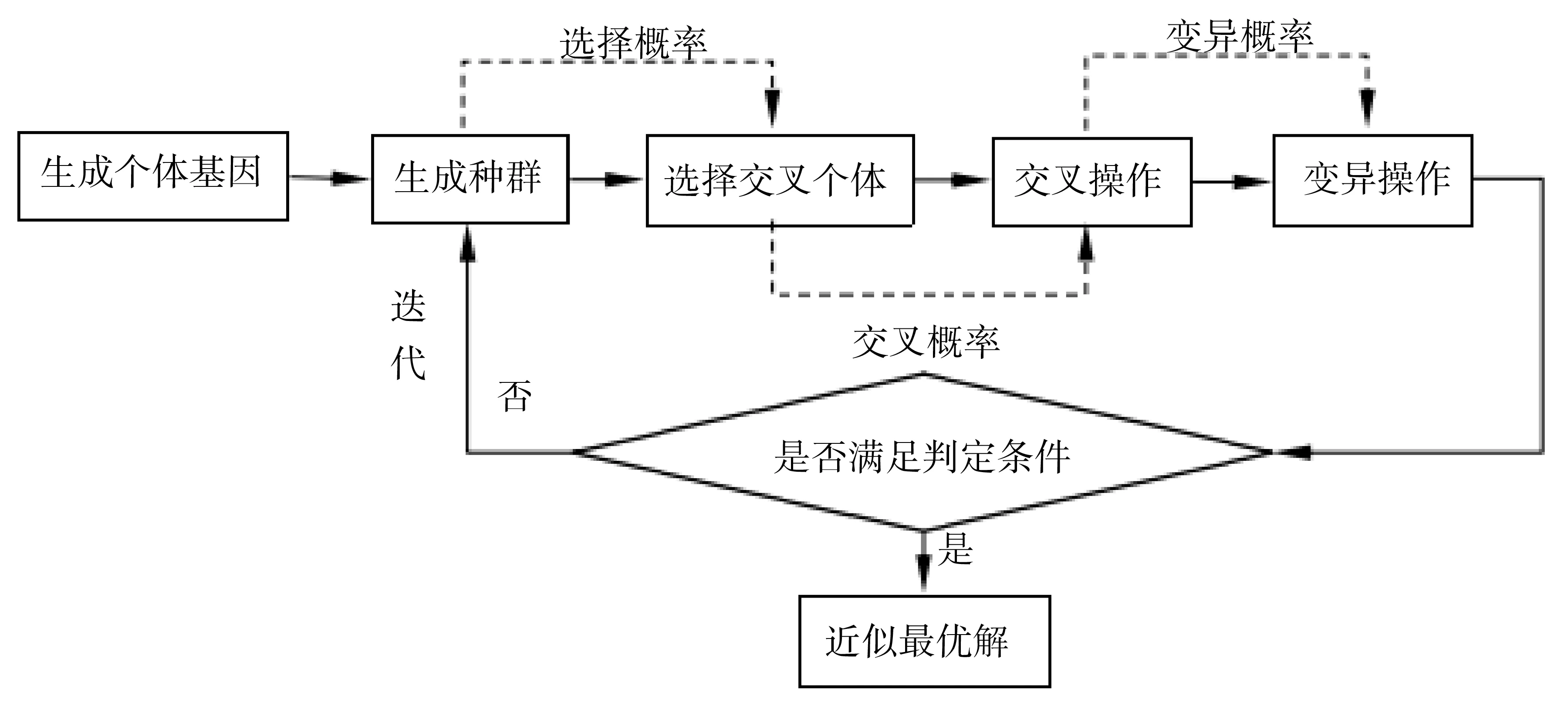
图1 遗传算法优化流程

1.2 PSGA算法分析

与其他智能优化算法相比，GA算法可以使搜索范围快速遍布整个可行解空间，可以在理论意义上更加快速地发现最大值或最小值所在位置.但是从另一方面来看，GA算法也存在很明显的局限性.例如：遗传算法的个体基因构成往往针对于具体工程问题，在问题规模较大的情况下，GA算法的基因构造也会更加复杂，会使编程规模和求解效率受到显著影响；GA算法的1个运行单位至少包含3个运算步骤，当总遗传个体的数量较多时，算法的整体性能也会受到显著影响.

1.2.1 PSGA算法结构

基于上述遗传算法的特点分析，本文对传统遗传算法的结构与流程进行了重新设计，提出了一种新型变种群极搜索遗传算法(PSGA).PSGA算法的结构逻辑是：首先在种群中找到需要繁殖的个体特征值，一般为最大值和最小值；之后，对个体特征值进行变种群繁殖，在繁殖过程中增加对繁殖方向进行实时控制的调节因子，即AF因子，使最大值的种群繁殖向当前最优值所在的周边区域发散；同步地，使最小值的种群繁殖向整个解空间进行发散；通过多代迭代后，个体的搜索范围在尽可能最大限度地覆盖解空间的同时，也已经尽可能最大限度地探索到了更加精确的最优解.PSGA算法的结构流程如图2所示.

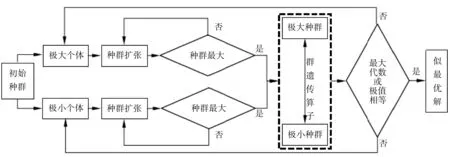
图2 PSGA算法结构流程

1.2.2 PSGA算法的适应度调和因子

· 堪萨斯城(Kansas City Plant)国家安全园区负责39种重要非核组件的生产，包括点火、保险和控制组件；

PSGA算法中对“两极”的控制以及对最大适应度种群和最小适应度种群搜索空间大小的控制是通过种群适应度调和因子(AF因子)来实现的.AF因子调和能力的强弱与种群进化最大代数、当前进化代数、当前种群中的最大适应度值和最小适应度值以及当前个体适应度值相关.当进化过程中任意一代中的两极个体进行新的种群繁衍时，其所生成的子个体分布位置即由AF调和因子来控制.当进行繁殖的个体适应度值更趋向于目标函数理想值时，AF调和因子会控制其产生的子个体分布位置更集中于该个体周围的空间范围，以确认是否该个体的周围空间还存在更好的个体；相应地，当进行繁殖的个体适应度值与目标函数理想值相差较大时，AF调和因子会让被繁殖个体生成的子个体分布空间更大，使新的个体能够在新的空间中探索更好的适应度值，其大小由以下公式确定.

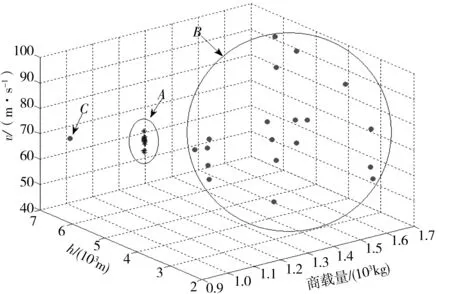
图3 适应度因子调和下的种群个体分布

其中，FAF为调和因子，itermax、iter为极种群的最大进化代数和当前进化代数，fmax和fmin为当前代数中的最大适应度值和最小适应度值，f为当前个体的适应度值，m为调和指数，α、β为调和系数.

极种群中的个体按照各自的适应度值所确定的上述适应度调和因子来确定其分布的空间范围.

图3为1个PSGA算法算例中进化到最后一代的种群分布图.可见适应度调和因子在控制种群个体分布空间范围上的效果.A区域中的星号非常集中，在一个很小的空间中排布，代表这些个体的适应度值更趋于符合问题求解的理想解，这时AF调和因子在某个体的繁衍过程中将生成的新个体的分布控制在围绕该个体的很小区域内，即出现了A区域中的效果.由图3中同样可见，圆点的分布空间要比星号广了很多，甚至其部分个体分布得更远，如C点所示.这说明在进行某个体的繁殖过程中，该个体的适应度值相对于问题的理想解相距很远，这时通过AF因子的控制，使新生的个体在空间分布上更广，更能有机会探索到更好的适应度值.

2 PSGA算法运行性能分析

为了更加清楚地了解PSGA算法的运行特性，以下将利用PSGA算法对不同复杂度的标准测试函数最优解搜索过程进行考察，通过使用Matlab8.3平台进行编程实现.

2.1 Booth’s function测试

Booth’s function函数的基本形式为

f(x,y)=(x+2y-7)2+(2x+y-5)2,

其中，测试域为-20≤x≤20和-20≤y≤20.该函数有一个最小值，在(1,3)处取得最小值为f(1,3)=0.其三维空间如图4所示.

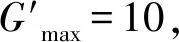
表1 Booth’s function函数PSGA算法运行10次最优解对比表Tab.1 Booth’s function’s optimal solution after 10 times operation with PSGA

由表1可见，在10次运算中使用PSGA算法求得的最优解最小精度为10-6数量级，其中有6次达到了10次运算中的最大精度10-10数量级，平均最优解的精度在10-7，为6.963 08×10-7,更接近函数已知的最优解F(x,y)=0；相对地，使用传统GA算法求解，在最优值的精度上就低了一些，最高精度在10-8数量级，最低精度在10-4数量级，平均精度为2.329 04×10-5.另一方面，从最优解的求解时间上看，使用PSGA算法所需要的时间最多为1.454 s，在连续10次运行中平均耗时为1.2931 s，普遍少于1.5 s，而相应地，在规定的2 s时限内，传统GA算法运行求解的最小值平均水平要明显低于PSGA算法.在限定时间内，平均运算效率PSGA算法较GA算法高出35.35%.这说明，PSGA算法的运行效率要明显高于传统遗传算法，在运行中能够快速收敛，在进化代数上要小于遗传算法，同时深度搜索能力更强，能够快速定位最优解的位置，求解质量更好.

2.2 Lévi function测试

Lévi function函数的基本形式如下：

f(x,y)=sin2(3πx)+(x-1)2(1+sin2(3πy))+(y-1)2(1+sin2(2πy)),

其中，测试域为-20≤x≤20和-20≤y≤20.该函数有一个最小值，在(1,1)处取得最小值为F(1,1)=0.其三维空间如图5所示.

图4 Booth’s function测试函数三维图

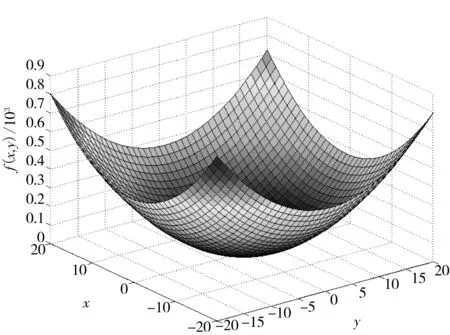
图5 Lévi function测试函数三维图

在使用PSGA算法进行优化求解时，预设参数与Booth’s function函数相同，同样连续运行10次，对比遗传算法运行数据如表2记录所示.

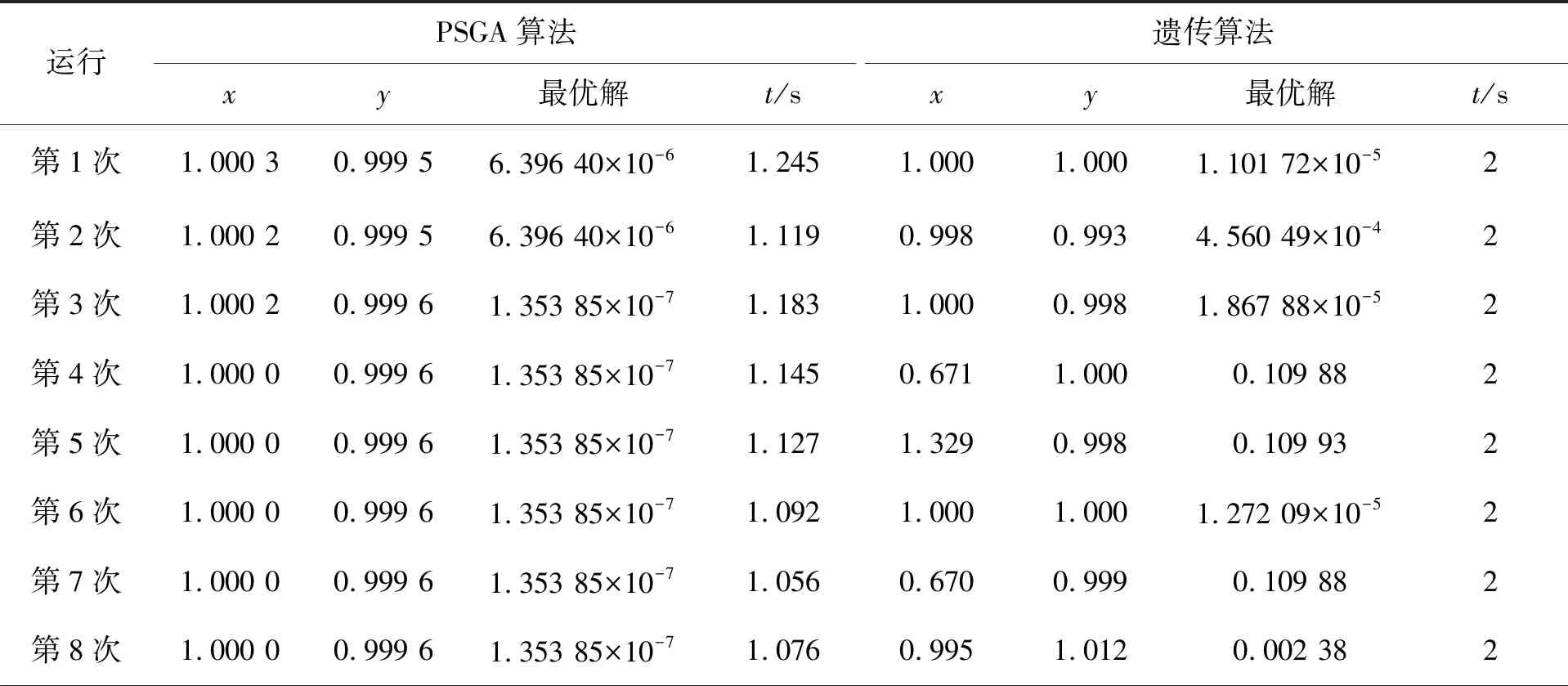
表2 Lévi function函数PSGA算法运行10次最优解对比表Tab.2 Lévi function’s optimal solution after 10 times operation with PSGA

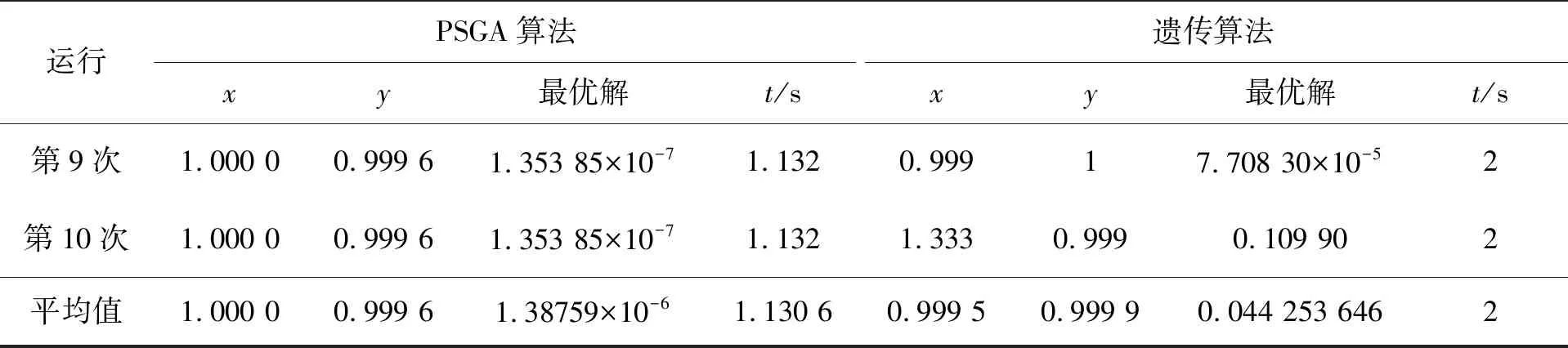
续表2Continued Tab.2

由表2可见，在Lévi function函数的寻优过程中，PSGA算法与GA算法的平均运算精度都有所下降，但在规定时间内，PSGA算法的精度基本稳定在10-7量级，在10次运算中有8次达到了10-7量级，最小精度为10-6次数为2次，对比函数已知的最优解F(1,1)=0可知，在对精度要求不是极高的应用环境下，PSGA算法10次运行所求得的最优解是有效的；相对地，可以看到GA算法在精度上下降了很多，求解平均精度只有10-2，平均值为0.044 253 646，最高精度也只有10-5，最低精度下降到了10-1数量级，比PSGA算法的平均精度低很多.同时这也说明在时效性要求高的应用场景中，传统遗传算法的寻优效率会有一定局限性.此外，从最优解求解时间上看，使用PSGA算法最多为1.245 s，平均耗时为1.130 6 s，平均运算效率比GA高出43.50%.说明PSGA算法的运行效率和求解质量更好.

3 PSGA算法在通航物流配载系统优化中的应用

本文以通航物流配载系统的配载效能为目标，以飞行高度、飞行速度、商载重量、燃油质量、大气压强以及通用飞机自身的设计特性为主要参考因素，建立单位任务配载经济效能优化模型，以某型号通航货运飞机的实际状态参数为例，使用PSGA算法对模型进行求解.

设PSGA算法的目标函数为

Fmax=max{Feco},

其中，Feco={Fe1,Fe2,…Fei…}，且有

其飞行状态环境约束为

其中，

Feco为经济效能水平指数，Ml、Mp、Ms分别为某型通航飞机的燃油载量、飞机空重和飞机商载，KAB为执行一次单位通航物流任务从A点到B的飞行距离，α、β为配载系数，α>0、β>0，令α+β=1，C0、C1、C2、C0D、C1D、C2D为与通用飞机飞行特性相关的状态系数，vmax为飞机最大巡航速度，hmax为飞机最大巡航高度.

设目标函数为PSGA算法的个体适应度函数，种群扩张的最大代数为itermax，当前代数为iter，个体当前适应度为ad，本代中最大适应度为admax，最小适应度为admin，当前代初始个体为adini.

设PSGA算法的AF因子为F(α,β)，则有

相关参数初始值为

C0=0.013,C1=0.000 06,C0D=0.003 6,C1D=-0.067,C2D=0.18;θ=0°,

Mp=3 402,vmax=100,hmax=6 000,Mmax=5 250,

itermax=50,m=2,α=10,β=3.

根据以上配载状态设计和算法参数设置，在Matlab8.3软件环境下进行编程和数据分析.

图6所示为单位通航物流配载任务效能极小值种群的进化过程比较图.图6a是极小值衍生的初始种群空间分布图，图6b是极小值种群经过30代进化后的空间分布图.图6中的任意一个三角形标志都代表了一个满足问题要求的配载状态解.根据2幅个体种群进化对比图，初代中的三角形个体随机分布在解空间的不同位置，呈现局部聚集和全局发散的态势，有些个体甚至分布到了空间的角落部分，这是在自适应调和因子的作用下，种群具备了较强的解空间开拓能力所致；而在经过若干代的迭代之后，个体已经完成了大部分解空间的探索过程，找到了相对初代更加优秀的解和相应的局部解空间，这时种群整体体现出来的是总体适应度水平更高且在解空间中呈现集中性、聚集性的特点.图6b中所示的三角形区域相较于图6a更加聚集，即是适应度调和因子在迭代后期进行有向性调节的结果.

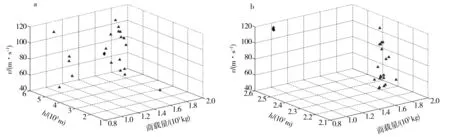
a.第1代极小值种群分布；b.第30代极小值种群分布.

图7是单位通航物流任务配载效能水平优化曲线对比图.图7a点线为使用经典遗传算法进行优化的过程.图7b中的连续实线为使用PSGA算法进行优化的过程，2种算法都是在最大种群规模为20，最大进化代数为50的同等环境下进行的，其中遗传算法的3个算子的概率为：选择概率0.6、交叉概率0.6、变异概率0.1.两种算法都进行10次运算后取平均值.据图7b可见，在PSGA算法中的种群适应度值跨度明显更大，这说明PSGA算法在各代的进化过程中解空间搜索范围更大；同时在图7中也可以看出遗传算法的进化曲线更缓，PSGA算法的曲线则更加陡峭，这说明PSGA算法在进化中的最优解搜索速度更快，但由于搜索范围更大，PSGA算法不易陷入局部最优解.由图7c中的联合比较图可见，PSGA算法在第10代搜索到的最优效能水平指数为537.931 0，遗传算法在第35代搜索到的最优效能水平指数为536.476 3，可见PSGA算法在同种群条件下的收敛速度更快，寻找到的最优解质量更好，运行效率更高.

a.GA算法；b.PSGA算法；c.GA算法/PSGA算法.

在上述所搜索到的最优个体中，任务载机在飞行状态稳定在高空2 212.55 m，飞行速度维持在215.21 km/h，商载量965.13 kg，燃油量836.92 kg，最远飞行距离为1 442.90 km时的单位通航物流配载任务效能指数达到最优.

4 总结

设计和提出了一种新型变种群极搜索遗传算法(PSGA)以及为该算法所设计的适应度调和因子(AF因子).通过以2类不同复杂度的基准测试函数为例进行MATLAB编程，比较了同环境下PSGA算法与GA算法的时间效率和求解精度.根据测试数据表明，PSGA算法在效率和精度上要明显优于传统GA算法.通过将该算法和传统GA算法同时应用于通航物流系统配载效能优化问题，比较两者在收敛效率和求解精度上的差别，说明了PSGA算法在时间效率要求较高的应用场景下,其有效性和适用性均比传统GA算法要好.