一种改进的协同过滤推荐算法

李昆仑，戎静月，苏华仃

(河北大学 电子信息工程学院，河北 保定 071000)

近年来随着云计算、大数据、互联网的快速发展，电商也随之发展起来并得到了用户的认可和应用.随着电商用户及商品数目的增多，为了使用户在大量的商品中快速、方便地找到符合自己需求的项目，同时电商将用户需要的项目推荐给用户，许多学者进行了相关的研究，个性化推荐系统[1]应运而生.推荐算法是推荐系统中最重要的部分，算法的优劣直接影响推荐效果的好坏.传统的推荐算法已经很难满足用户的个性化需求，目前主要的推荐算法有协同过滤推荐算法[2]、基于内容的推荐算法[3]、基于关联规则的推荐算法[4-5]、混合推荐算法[6]等.其中协同过滤推荐算法不需要考虑具体推荐内容，技术上易于实现，所以应用最为广泛.但是也面临着一些难以解决的问题，比如数据缺失引起的数据稀疏性问题[7]、新用户加入引起的冷启动问题[8-9]、用户兴趣变化引起的用户兴趣漂移[10]等问题.

基于用户的协同过滤推荐算法主要是根据用户的历史评分数据，用已评分的数据计算用户相似度产生近邻集，从而产生推荐.随着电商项目的迅速增加，推荐系统中用户和产品的数量持续增加，用户购买量及评分数的增长远远比不上电商项目的增长速度，当用户和产品数量达到千万或更多时，U-I(用户对产品的评分) 矩阵将变得十分庞大.然而，推荐系统中每个用户对产品的评价是有限的，因此U-I 矩阵十分稀疏，从而产生数据稀疏性问题[11].在个性化推荐系统中，用户对产品的喜好程度通常可以由其对历史产品的评价信息来反映.面对稀疏的评估数据，推荐系统难以准确地判断用户偏好.

针对数据稀疏性问题，传统的解决方案是用现有数据的均值填充缺失的数据[12]，但是这会给预测结果带来很大误差,进而影响推荐系统的推荐精度.对此文献[13]提出的改进的算法中加入了用户兴趣相似性和评分相似性；文献[14]给用户的属性分配权重加入到相似度的计算当中，提出了一种基于用户多属性的协同过滤算法；文献[15]将用户属性、用户兴趣与传统的相似度相结合，调整不同的权重，通过动态选择近邻集的方法来降低数据稀疏性.上述方法都是通过加入一些新的因素，调整不同因素所占的比例，与传统相似度相结合来提高推荐精度，虽然数据稀疏性在一定程度上得到了缓解，但是计算量却明显增大.

另一方面，冷启动问题也会引起推荐系统推荐精度差的问题.冷启动问题包括用户冷启动问题和项目冷启动问题[16].用户的冷启动是针对推荐系统的新用户，他们对有些产品的评价记录很少甚至没有，该推荐系统无法从少量的评价数据中获得新用户的兴趣爱好，因此无法准确推荐.项目冷启动意味着当新项目添加到系统时，很少被用户选中甚至没有.针对这些新项目，系统很难找到合适的办法来准确向用户推荐.由于本文主要针对基于用户的协同过滤推荐算法，主要研究用户冷启动.针对冷启动问题，目前解决冷启动问题的方法很多，常用的方法主要包括以下3个方面：1)向新用户随机推荐或推荐热门产品[17].随机推荐之后，根据用户的反馈不断改进用户的偏好模型，与此同时可能给用户推荐的产品用户都不喜欢，这样会降低用户对系统的信任度.随机推荐的改进是向用户推荐热门产品，但仍然无法做到个性化推荐；2)传统协同过滤的改进方法[18]，对用户或产品间相似性度量方法的改进；3)结合机器学习的方法[19].对此文献[20]提出加入用户的注册信息，利用用户的注册信息进行推荐.文献[21]提出利用用户的社交网络账号，对新用户推荐其好友喜欢的物品.由于涉及用户隐私，数据获取并不容易实现.

针对数据稀疏性和用户冷启动问题，本文首先通过改进的填充方式填充原有的稀疏数据，充分利用有评分的数据，避免了一个或几个用户对数据填充的不准确，提高了填充精度.然后在相似度的计算中加入用户的属性，如年龄、性别、职业、邮编，这样可以避免新用户的加入造成的冷启动问题.实验结果表明，与传统方法相比，该方法具有更高的推荐精度.

1 推荐系统中常用的相似性计算方法及评分预测方法

传统的基于用户的推荐算法中最重要的工作是寻找到目标用户的近邻集[22]，通过近邻用户向目标用户进行商品推荐，因此近邻用户的寻找精度将直接影响推荐效果.近邻用户是通过相似度的计算来确定的，将相似度按照由大到小的顺序排列，取前N个用户得到目标用户的近邻集.推荐算法大致可分为3步：1)获取用户-项目评分矩阵，对其数据进行预处理；2)通过用户/项目之间的相似度获得目标用户的最相似近邻用户集；3)根据所有近邻用户对目标项目的评分，来预测目标用户对目标项目的评分从而进行推荐.

1.1 常用相似度计算方法

相似度计算是寻找近邻用户的关键，相似度计算主要包括余弦相似度、修正的余弦相似度、皮尔森相关系数、各种距离相似度等.

1.1.1 余弦相似度

余弦相似度主要是通过计算2个向量的夹角来判断其相似性，又称为夹角余弦[23]，取值在-1～1，夹角余弦越大，表示2个向量的夹角越小，则其相似程度越高.具体的计算公式如下：

(1)

1.1.2 修正余弦相似度

余弦相似度没有考虑用户的评分尺度的影响，即有些用户对所有项目的评分相对较高，而有些用户要求严格对所有项目的评分相对较低，例如(5,5,5)和(1,1,1)的余弦相似度值为1，2个向量将会非常相似，但实际情况恰好相反.因此提出修正的余弦相似度，将用户的平均评分引入计算公式，减少评分尺度的影响，具体计算公式如下[24]:

(2)

1.1.3 皮尔森相关系数

皮尔森相关系数，又称为相关相似性，需要找到2个用户共同评过分的项目，然后计算其相关性[25]，计算公式如下：

(3)

1.1.4 距离相似度

前面介绍的余弦相似度主要关注向量方向的差异度，而距离相似度关注2个点的距离，距离越近相似度越大.距离包括欧式距离、曼哈顿距离、切比雪夫距离、闵可夫斯基距离、马氏距离等，因为距离和相似度大致成反比.距离相似度公式如下：

(4)

1.2 常用评分预测方法

根据相似度确定目标的近邻用户之后，需要通过近邻用户对目标项目的评分进行评分预测，评分预测方法有平均评分法、加权平均评分法、偏移的加权平均评分法.

1.2.1 平均评分法

平均评分法是根据近邻用户对目标项目所有评分的均值直接作为目标用户对目标项目的评分[26].设近邻用户为U=(u1,u2,…，um),项目为I=(i1,i2,…,in)，具体公式如下：

(5)

1.2.2 加权平均评分法

平均评分法将所有近邻集中的用户评分数据取均值作为目标评分，但是忽略了相似度权重的影响，与目标用户相似度越高，评分预测的结果越准确，所以加权的平均评分法引入相似度的权重，s(u,k)为目标用户u与近邻用户k的相似度[27]，具体公式如下：

(6)

1.2.3 偏移的加权平均评分法

(7)

2 传统推荐算法中几个关键部分的改进

针对传统的协同过滤推荐算法进行优化，对原始数据集进行预处理，将评分数目远小于项目数目的数据过滤掉，进行初步降维.由于数据的稀疏性问题，需对数据集中缺失的数据部分进行填充，根据用户评分习惯进行层次聚类，并将用户基本信息和共同评分项所占的比值作为计算相似度的权重.通过 Slope-one[29]算法计算前k个最相似用户对缺失数据的填充值，同时加入相似度权重得到最终填充值.针对填充后的数据，首先在传统相似度的基础上，加入用户基本信息作为相似度的权重，其次通过Sigmoid函数引入用户项目评分的时间戳对相似度的影响，获得目标用户的最近邻集，最后利用改进后的相似度对目标用户进行推荐.

2.1 相似度计算

用户相似度是寻找近邻用户集的依据，传统的相似度计算方式是以用户具有相同的兴趣为前提，仅通过用户对项目的评分来计算相似度，不考虑不同用户的属性，如性别、年龄、职业等对用户相似度造成的影响，由此得到的用户相似度准确度不高.本文基于传统的相似度计算方式，首先加入编码后的用户信息求得欧氏距离，其次引入指数函数作为相似度的用户信息权重，针对时间改变造成用户兴趣漂移的问题，加入评分时间戳的影响，最后引入 Sigmoid 函数作为时间戳的函数，表明评分时间越相近，用户的相似度越高，权重越大.

函数表达式为

(8)

传统的相似性用皮尔森相关系数

(9)

改进后的相似度计算公式

(10)

β=e-Db(u,v)，

(11)

(12)

其中Db(u,v)是对用户性别、年龄、职业编码后计算的欧式距离，ru,b为对用户u的信息进行编码后的向量，β表示用户信息所占的权重，s(u,i)为用户u对项目i的评分时间戳所占的权重大小，评分时间越相近评分权重越大，则相似度越高，sim(u,k)为最终相似度的计算公式，ru,i为用户u对项目i的评分.

加入用户属性和时间戳的相似度，可以在一定程度上减少新用户加入造成的冷启动问题，使得推荐效果更佳准确.

2.2 数据填充

由于用户-项目评分数据稀疏性问题，在计算相似度寻找近邻用户会产生很大误差，造成推荐效果不佳，因此将评分数目远小于项目数目的数据进行过滤、删除，然后对缺失的数据进行填充，传统填充方式虽然完成了对缺失数据的填充，但推荐效果并没有明显改善，对此本文在传统填充方式上，引入用户属性和相似度权重，利用 Slope-one 算法对填充算法进行改进.

根据用户对项目的评分信息，利用层次聚类，对用户数据进行聚类.根据用户对项目评分均值分成3类，即评分均值大于4的用户，均值小于2的用户，均值在2～4的用户，分别用Uo、Up、Un表示3个类别，分别代表积极、消极、中立态度的用户群体.

聚类过程如下：

分别对聚类后的每个簇进行缺失值的填充，对数据进行降维、减少计算量的效果.填充之前首先计算需要填充的用户和在同一个簇中其他用户的相似度，然而传统的相似度计算方式是利用评分数据计算欧氏距离，当新加入的用户没有评分信息时，无法计算距离，对此本文引入用户的基本信息来计算相似度.

对用户信息进行 One-hot编码和LabelEncoder编码，利用编码后的用户信息，基于欧氏距离计算相似度，同时加入共同评分项作为权重，获得相似度值.利用Slope-one算法计算前m个用户对缺失值的填充数据，并加入相似度的权重获得最终填充数值.通过设定相似度阈值，来筛选出相似度高的用户，过滤掉相似度低的用户.如果阈值过小，会降低填充精度，如果阈值过大，会导致计算量增大，因此，需要多次反复实验，在保证合理的计算量的前提下，尽可能提高填充精度，确定最终的阈值m.

Slope-one算法原本是计算不同项目之间的评分差的一种线性算法，根据用户对某个项目的评分预测另一个项目的评分.本文利用Slope-one算法的思想，通过用户a、b的平均评分差，及用户a对项目I的评分，计算对项目I无评分的用户b的填充数据.具体计算公式如下：

(13)

Pbi=rai-R(a,b),

(14)

其中,R(a,b)为用户a、b对所有共同评分项目的平均评分差；N(a)为a用户评过分的项目；N(b)为b用户评过分的项目；N(a)∩N(b)是a、b均评过分的项目集合；rai为用户a对项目i的评分，rbi为用户b对项目i的评分;|N(a)∩N(b)|是a、b均评过分的项目数.Pbi是用户b对项目i评分的填充数据，rai为用户a对项目i的评分.

各缺失值的填充计算公式如下:

(15)

(16)

simab=Db(u,v)×αu,v,

(17)

(18)

(19)

其中Db(u,v)为编码后的欧式距离，rb,u,i为用户u的信息编码与对项目i的评分组成的向量，αu,v为共同评分项所占的权重，simab为用户a与用户b加入用户信息和共同评分项后的相似度，Pbj为用户b对项目j的缺失值的填充值，Poj为最终的填充值.

由以上分析可知，根据用户评分习惯对用户进行层次聚类，达到了初步降维的效果，并且聚类后求相似度的准确度有所提高.在计算相似度时加入用户的基本信息，改善了冷启动的影响.加入共同评分项的权重，进一步提高了相似度的准确度.通过均值填充，减少评分尺度的影响，并且加入相似度权重，提高了填充值的精度,从而能更准确地推荐.

算法如下.

Step1：引入用户性别、年龄、职业这些基本信息.对用户进行层次聚类，最后得到3种不同的用户群体；

Step2：对不同的用户群体运用公式(17)计算要填充的用户与其他用户的相似度，按从大到小取前m个值，组成一个近邻用户集；

Step3：通过公式(18)，利用上述集合中的向量对目标向量进行缺失值的初步填充；

Step4：引入相似度权重，对目标向量进行最终的缺失值填充；

Step5: 重复步骤1、2、3、4，直到数据集填充完毕.

2.3 评分预测

通过相似度的计算得到了目标用户的近邻用户集U=(u1,u2,…,um)，根据每个近邻用户对目标项目的评分利用填充公式 (18)和(19)对目标项目进行评分预测，第k个近邻用户对第i个目标用户的预测结果为rk,i，然后利用预测公式(20)对最终的目标项目进行预测评分，然后循环此步骤，直到对所有的目标项目评分完成预测，最终形成推荐.

最后根据改进的相似度的计算方法，用TopN取前N个最相似的用户进行推荐.

(20)

3 实验结果与分析

首先简单介绍本文涉及到的实验环境和选取的数据集以及实验的评价指标，然后根据该数据集将本文所提出的方法和改进前的方法进行对比分析.原始数据的稀疏度是0.891 6，经过2次实验，其中第1次实验的数据稀疏度是0.888 2，第2次是0.892 5.

3.1 实验环境和数据集介绍

实验使用的计算机的配置是Intel Core i5-7200的CUP，8GB运行内存，Windows 10家庭中文版64位操作系统，编程语言使用Python语言，版本为Python3.6，编辑器用的是Jupyter Notebook.

本实验采用的是由Minnesota大学GroupLens研究小组提供的100 K的MovieLens数据集，它还有1 m、20 m等几个版本.数据集主要包含2部分数据：1)用户对项目的评分数据，该数据集包含943个用户，1 682部项目，100 000条评分数据，评分为1～5分，且每个用户项目评分次数不少于20次.2)用户基本属性数据，该数据集包含用户的性别、年龄、职业、邮编的基本信息.本次实验采用2次5折交叉验证,分别计算系统的MAE值，得到最终的实验结果.

3.2 实验评价指标

目前推荐算法性能的评价指标主要有平均绝对误差(MAE)、均方误差(MSE)、查全率、查准率、F1-score等.此系统采用平均绝对误差MAE作为评价指标，MAE为预测值和真实值之差，表明其值越小，则预测的结果越准确.假设推荐系统对项目的预测评分集合为{r1,r2,r3,…,rn}，项目的实际评分为{p1,p2,p3,…,pn}，则用户MAE值可以用式(21)表示

(21)

系统的MAE可以用式(22)表示

(22)

3.3 实验结果与分析

3.3.1 第1轮实验结果

图1描述的是聚类前后，均采用改进的填充方式进行填充，用皮尔森系数计算相似性时系统的MAE值随近邻用户取值的变化曲线.其中NCUFP曲线为聚类前系统的MAE曲线，CUFP曲线为聚类后系统的MAE曲线，从图1中可以看到，训练集经过聚类后系统的MAE值随近邻用户的变化趋势比较平缓，并且整体比聚类前的MAE值低，这样可以选择少量的近邻用户，降低系统的成本，并且通过聚类，降低了数据的维度，大大减少了计算量.当近邻用户数在200～400时，在计算量少和系统成本低的前提下，系统的MAE值趋于最低，当相似用户大于400时，聚类效果不太明显，但系统的成本和计算量会增加，所以选择近邻用户数为350，通过聚类得到的模型最佳.

图2描述的是不对用户进行聚类，分别用均值填充和改进填充进行填充，并且用皮尔森系数和改进的皮尔森系数求相似度得到的系统的MAE随近邻用户的变化曲线的对比图.NC-MFPS曲线代表用均值填充，皮尔森计算相似性得到的系统MAE曲线,NC-UFPS曲线代用改进填充方式填充，用皮尔森计算相似性得到的系统MAE曲线；NC-FUPS曲线代表用改进填充方式填充，改进的皮尔森相似度计算相似性，得到的系统MAE曲线.

图1 聚类前后的MAE值对比

图2 不聚类改进填充相似度MAE值对比

针对图2中的NC-MFPS和NC-UFPS曲线的对比，可以得出通过改进后的填充方式比均值填充方式，在相同的相似度计算条件下，系统的MAE值明显降低了；针对NC-UFPS和NC-FUPS的曲线对比，可以得到通过改进后的方式计算相似度寻找近邻用户，系统的MAE值到在近邻用户取150～750时低于改进前的MAE.由于改进相似度的计算方式后得到的近邻用户更精确了，从而降低了系统的误差.由NC-FUPS曲线，可以看出当近邻用户在300～400的时候系统的MAE值最低.所以在选择合适的近邻用户的数量下，改进后的方式的推荐性能更优.同时，改进后的方式加入了用户的基本信息，更利于改善冷启动问题.

图3描述的是对用户进行聚类，分别用均值填充、改进填充进行填充，并且用皮尔森系数和改进的皮尔森系数求相似度得到的系统的MAE随近邻用户的变化曲线的对比图.MFPS曲线代表用均值填充，皮尔森计算相似性得到的系统MAE曲线，用MFPS表示；UFPS曲线代表用用改进填充方式填充，用皮尔森计算相似性得到的系统MAE曲线，用UFPS表示；FUPS曲线代表用改进填充方式填充，改进的皮尔森相似度计算相似性，得到的系统MAE曲线，用FUPS表示.

图3整体可以看出聚类后的系统MAE随近邻用户的增加变化不大，改进填充方式和相似度计算后明显降低了系统的MAE. 从图3中的MFPS和UFPS曲线的对比图，可以得到，通过改进填充之后系统的MAE值比改进前明显降低了，通过UFPS和FUPS的曲线对比，可以得到通过改进后的方式计算相似度寻找近邻用户，系统的MAE值低于改进前的MAE，由于改进相似度的计算方式后得到的近邻用户更精确了，从而降低了系统的误差.由FUPS曲线，可以看出当近邻用户在350～450的时候系统的MAE值最低.

图4描述的是对数据进行填充时，聚类前后系统的MAE值随填充选取的近邻用户的变化曲线.

图3 聚类后改进填充相似度MAE值对比

图4 聚类前后填充选取不同近邻用户MAE值对比

由图4可以看出通过聚类，系统的MAE值随近邻用户的波动比较平缓.并且通过2条曲线的对比，在近邻用户小于80时，通过聚类系统的MAE值要小于改进之前系统的MAE值.由此得到根据用户属性聚类降低了系统的MAE，提升了系统精度.实验过程中聚类最小的用户数是80，当近邻用户大于80之后聚类前后效果相差不大.

3.3.2 第2轮预测结果

经过第2次交叉验证实验，同样得到4个图，分别是图5、图6、图7、图8.同样得到用改进聚类、改进填充、改进相似度计算方式的方法得到不同系统的MAE值随近邻用户的变化曲线.

图5 聚类前后的MAE值对比

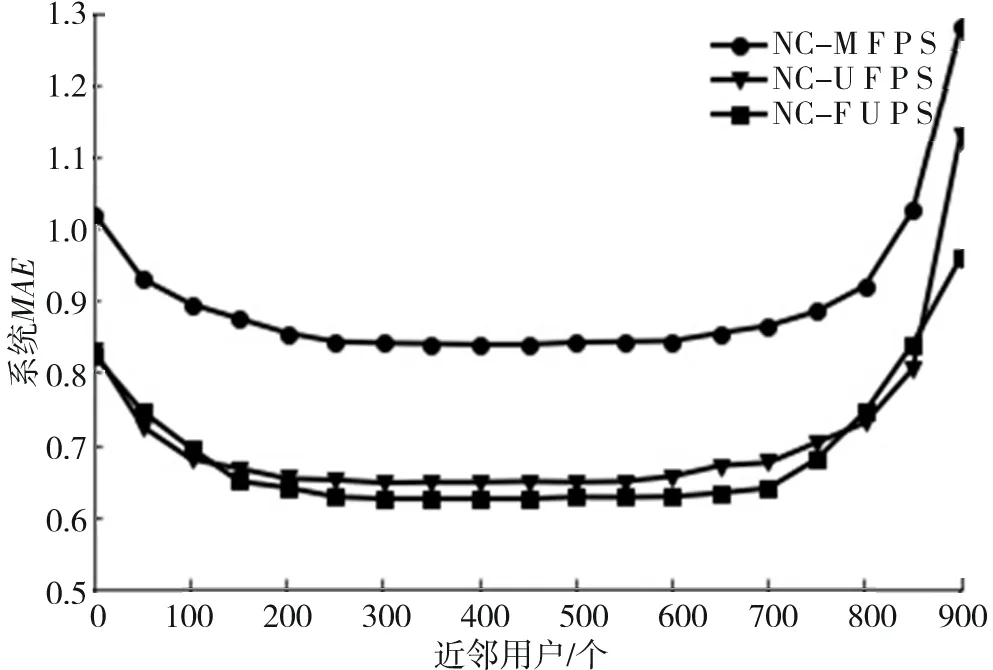
图6 不聚类改进填充相似度MAE值对比

通过对比实验1与实验2的结果，发现在选取相同近邻用户时实验2系统的MAE值要高于实验1系统的MAE值.由于对数据进行预处理后，第1次实验的数据稀疏度是0.888 2，第2次是0.892 5，第2次实验的稀疏度要高于第1次实验，可以得到，数据越稀疏，系统的MAE值越大，因此通过改进填充方式，降低数据的稀疏度尤为重要.

图7 聚类后改进填充相似度MAE值对比

图8 聚类前后填充选取不同近邻用户MAE值对比

4 结论

针对传统推荐算法在数据稀疏情况下存在的问题提出了一种改进的协同过滤推荐算法，首先针对数据缺失引起的数据稀疏性问题，该算法通过加入用户属性的影响，对填充方式进行了相应的改进并对数据进行填充，在一定程度上缓解了数据稀疏性带来的影响；其次针对相似度计算不准确导致推荐精度降低的问题，在传统相似度计算的基础上，加入用户基本属性和时间戳的影响，对相似度进行了相应的改进.经过实验验证，本算法提高了推荐的准确性，并且减少了冷启动给系统带来的影响，提高了系统的可扩展性.