基于机器视觉的镜面面形检测算法研究与应用

来 晓，宓霄凌 ，陈梦迟，王为民

（1.浙江中控技术股份有限公司，杭州 310053；2.浙江中控太阳能技术有限公司，杭州 310053；3.浙江大学控制科学与工程学院，杭州 310027）

太阳能作为一种可再生能源，具有储量大、清洁无污染等优点，成为新能源发电的研究热点[1]。塔式太阳能发电方式因其可储能、发电功率稳定的特点，得到了广泛关注[2]。

塔式太阳能集热系统主要由大量定日镜和装在中央吸热塔上的吸热器组成[3]。其中，定日镜是该系统中很重要的部件，它是将太阳能辐射聚焦到吸热器的能源聚集装置，其面形将直接影响到吸热塔上光斑的位置和质量。

目前针对镜面面形测量主要有接触式三坐标测量仪、激光扫描法等。这些方法具有测量准确，对待测面平滑度无要求等优点，但测量耗时长，效率低下，在大规模、大面积测量工作中不具优势[4]。条纹反射技术因其具有结构简单，价格低廉，非接触式和高测量精度等优点，现已成为面形检测技术的研究热点[5-8]。

值得注意的是，目前诸多条纹反射技术研究的测量对象的面积均小于0.1 m2，而目前已知的太阳能塔式光热电站的定日镜面积最小为1.14 m2，最大为178 m2[3]，对于这种大规模、大面积的定日镜面形测量，若采用传统条纹反射法，投影幕的尺寸大小应大于定日镜面积，相机视野须覆盖整个定日镜测量区域。而这种大面积投影设置和相机的选型及安装将严重制约定日镜生产装配方案的实施，提高定日镜面形检测的成本。

针对以上问题，在此基于广义时间解包裹算法[9]，结合坐标转换原理，对三维重建算法进行改进，开发了基于条纹反射的镜面面形检测算法，搭建试验装，并进行了验证。

1 基于条纹反射法的面形检测

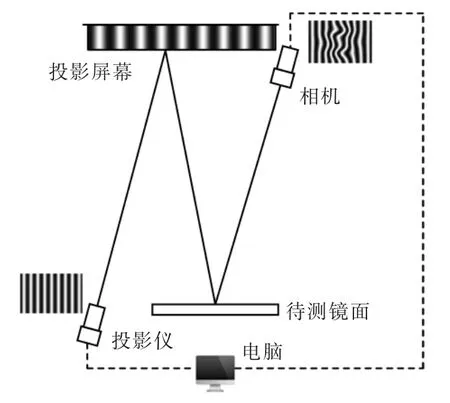
图1 条纹反射法原理Fig.1 Schematic of stripe reflection method

条纹反射法基于光线反射原理，是波前斜率测量方法之一。条纹反射法如图1所示，通过投影仪将调制好的具有周期性明暗间隔的条纹投射到平面投影屏幕上，将待测平面置于投影屏幕前，通过一台经过标定的相机拍摄经反射后的条纹图像，投射在投影屏幕上的调制条纹以一定相位变化，得到不同相位下待测平面反射后的条纹图像，将这些图像进行相位解调，即可获得被测物体沿x方向的高度数据，将条纹旋转90°后重复上述过程，可获得被测物体沿y方向的高度数据，进而获得整个被测物体表面面形数据[10]。

1.1 光栅投影系统

光屏坐标系如图2所示，在图2a中n轴平行于条纹方向。使用投影仪将调制不同光强的条纹投射至光屏上，光屏上条纹的光强为

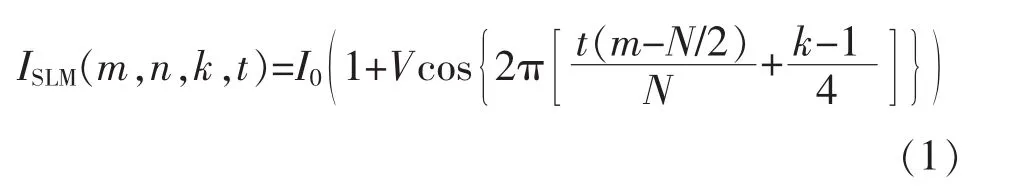
式中：I0为平均光强密度；V为条纹可见性；k为相 位步数序列，k=1，2，3，4；t为条纹的套数，t=1，2，…，s；t决定条纹频率，一般情况下条纹反射法取 t=1，2，4，8。由式（1）可知，对于任意一套条纹图，当m=N/2时，其亮度最大，即光屏中心处的亮度最亮。

假设：栅线距为λ0，点O处的相位为θ0，则光屏上任一点m处的相位θ，则有

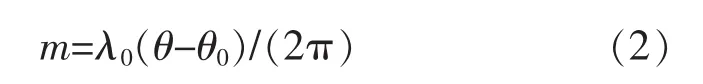
同理，使用一组竖条纹，如图2b所示，可以计算出

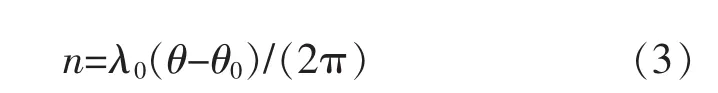
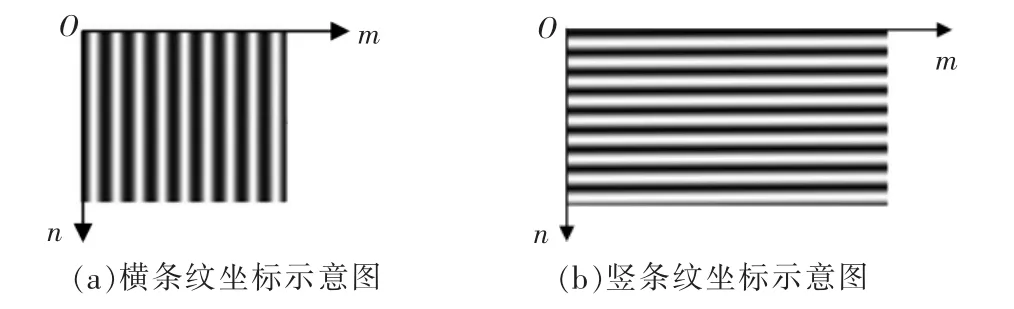
图2 光屏平面坐标系Fig.2 Plane coordinate system

1.2 四步相移法

采用条纹反射法对物体面形进行测量，由相机采集被待测镜面返回条纹图，从条纹图中提取相位，然后从相位数据得到待测镜面斜率数据，最后反演计算出待测镜面形。在此采用四步相移法[11-15]对条纹图进行解算。

采用带有90°移相的四步相移法，采集4幅带有相移的光栅图像，4幅图的相移分别为α1=0，α2=π/2，α3=2π/2，α4=3π/2，其灰度值分别为

式中：Ii（m，n）为第 i幅图的灰度值；I′（m，n）为条纹光强的背景值；I″（m，n）为调制强度；θ（m，n）为待求相位场。 由式（4），可得

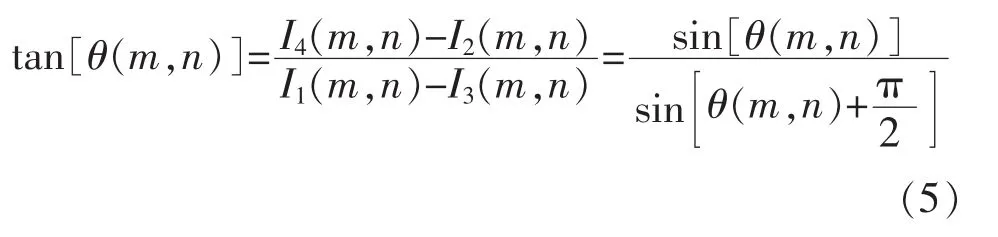
取反正切函数，可得相位主值为

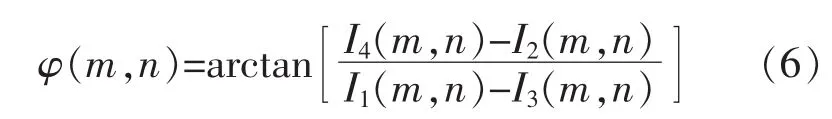
式（6）为四步相移法的基本公式，由其解出φ（m，n）的值域位于）区间。对于式（6）解得的 φ（m，n），需要对其进行模 2π 处理，将相位分布扩展到［0，2π］或［-π，π］，设 φ（m，n）经过模 2π 处理后，其值为 φ1（m，n），则其完整的相位值 θ（m，n）为

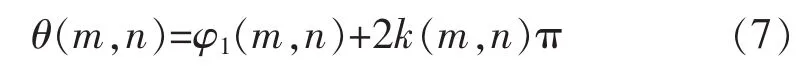
式中：k（m，n）为整数，表示点（m，n）处对应的 2π 整数倍，即点（m，n）所处的光栅条纹的周期数。相位解调即为求解 k（m，n）的过程。

在此采用时间相位展开算法[16]，对 φ1（m，n）进行解包裹计算，最终使得所有相位处于连续可导的真实数据状态。

2 三维形貌重建

2.1 面形拟合

系统基本测量原理如图3所示。在光屏上投射黑白相间的正弦条纹，条纹由被测镜反射后被相机捕捉。如果知道光屏上点T，对应的被测镜上点M和像素面上点P这3个点的坐标，就可以得到入射光线MT的单位方向向量i和反射光线PM的单位方向向量r，则可求得被测镜点M法向单位向量为

光屏、相机和被测镜的位置都是经过严格标定的。点O′是相机的透视中心，在相机的线性模型中，点P，点O′和M点三点共线，则点M的坐标可以通过直线PO′的方程与被测镜方程联立得到。而光屏上点T的坐标则经过四步相移算法和图像处理得到。在求解被测镜面形方程时运用迭代算法求得与实际情形比较吻合的被测镜方程。

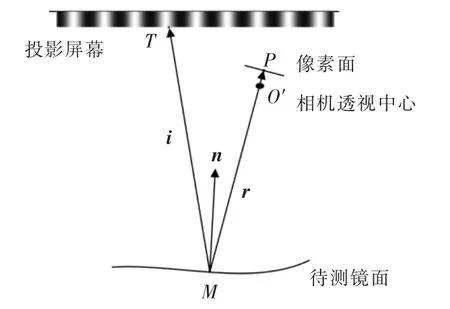
图3 条纹反射法系统测量原理Fig.3 Schematic of the fringe reflection system measurement

如图3所示，将像素平面上点P，相机入瞳中心点O′以及对应光屏上的点T的坐标变换到镜面坐标系中进行计算。在镜面坐标系中，被测的定日镜方程

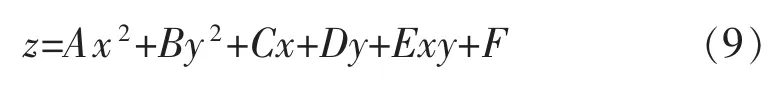
式（9）与直线PO′联立，即可得到被测镜点 M的坐标（xm，ym，zm），结合点 P 和点 T 坐标，可以得到入射光线、反射光线的单位向量r和i，则根据式（8）求得被测镜点M单位法向量n为

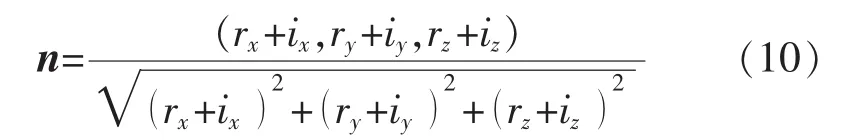
另外，将被测镜方程改写为

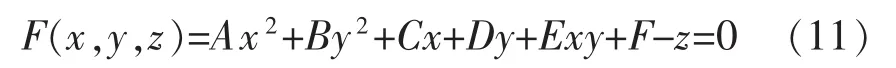
则镜面上点M的法向量为

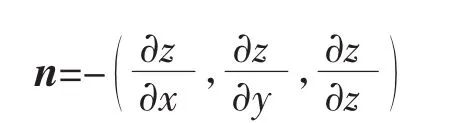
其中

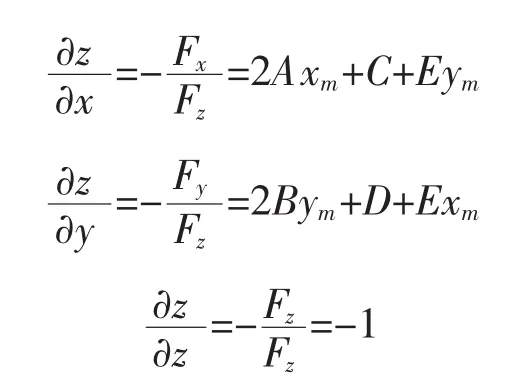
可得点M理想的单位法向量n′为

运用法线方向一致来拟合实际的被测镜方程即

则有

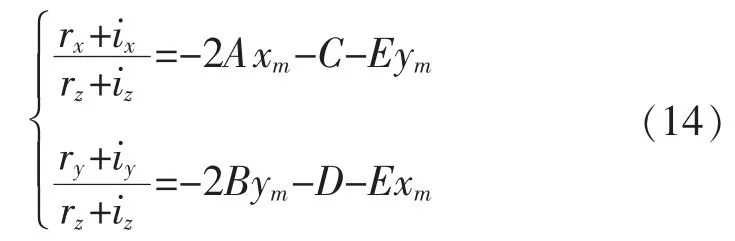
为了求得式（14）中各参数，在“活跃像素”中选取N的点，得到2个超定方程组，即

其中

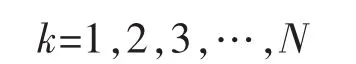
使用最小二乘拟合算法获得各参数值。

2.2 三维形貌重建

系统坐标系如图4所示。

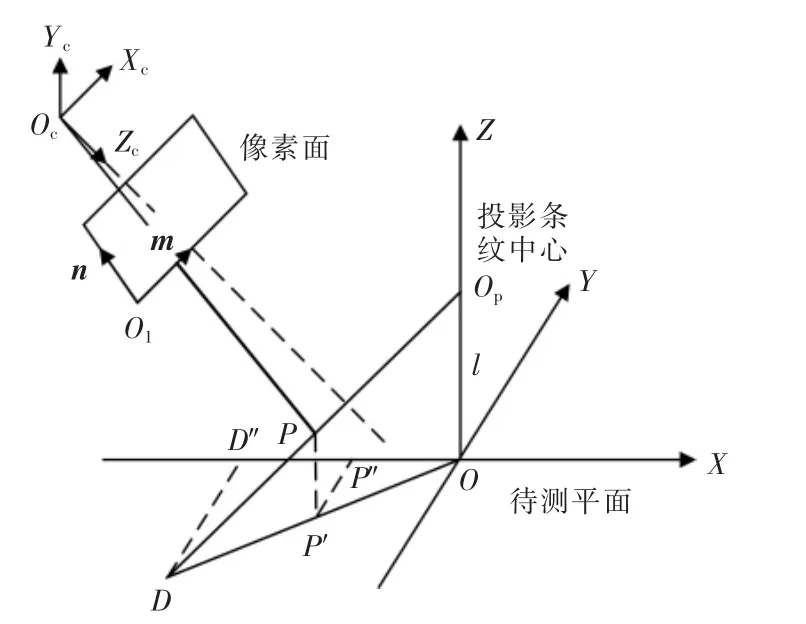
图4 系统坐标系Fig.4 Coordinate system

图中，Ωw为参考坐标系，Ωc为摄像机坐标系，Op为投影中心，Oc为光心；mO1n为摄像机成像面坐标系。OXYZ为参考坐标系，即Ωw根据投影装置建立：XOY平面平行于投影面，Y轴平行于光栅条纹，Z轴经过投影中心Op。

用旋转矩阵Rw和平移矩阵Tw描述Ωw与Ωc之间的位置关系。设物点P为待测平面上一点，其在参考坐标系 Ωw中的坐标为（X，Y，Z），在摄像机坐标系 Ωc中的坐标为（Xc，Yc，Zc），有

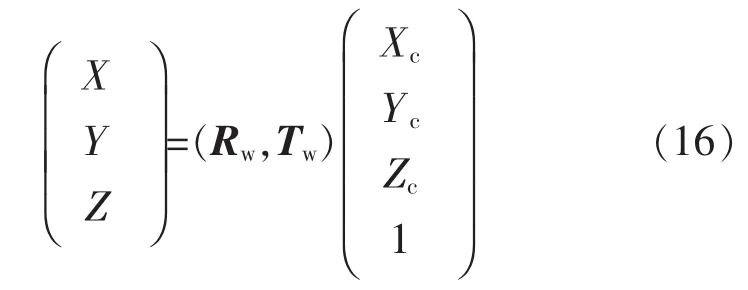
其中

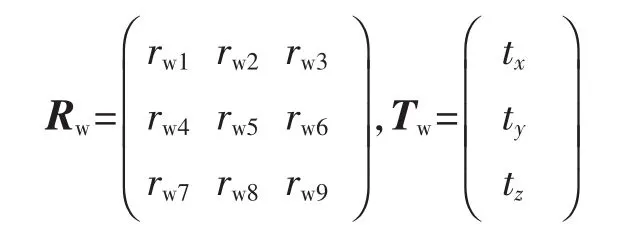
式中：Rw为单位正交旋转矩阵；Tw为平移矩阵。

图4中，根据三角形相似，可以得出

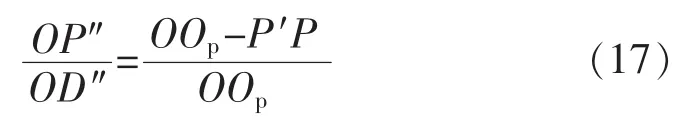
其中

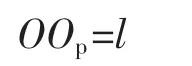
式中：P′P，OP″分别为点 P 的 Z，X 坐标。 D"D 平行于光栅方向，所以两点的相位相等，也等于点P的相位 θ，故

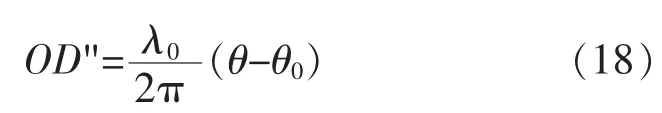
式中：θ0为原点的相位；λ0为栅线节距。由式（17）和式（18），可得

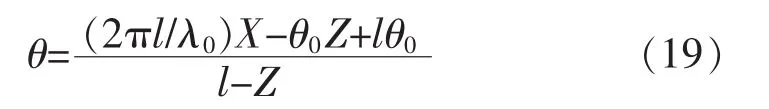
代入式（16），有

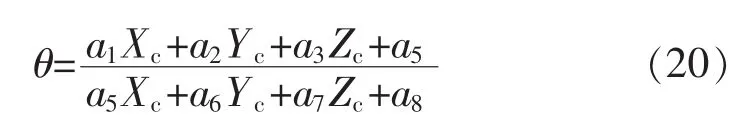
式中：a1，…，a8为参数，由标定获得，即

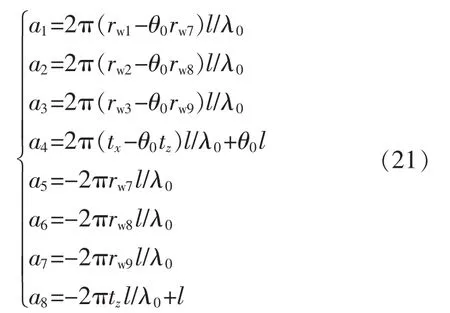
由此可得点P的（X，Y，Z）坐标，从而完成三维形貌的重建过程。

2.3 数据拼接算法

由于大面积镜面制作工艺复杂，成本高昂，所以大面积镜面一般由小镜面拼接而成。试验用20 m2定日镜如图5所示。由图可见，该定日镜由4面小镜拼接而成，每面镜子的尺寸为2.66 m×1.88 m。为保证测量精度，在此使用4个相机对其反射条纹数据进行采集，将相机采集的数据拼接起来，并采用条纹反射反演算法对其面形数据进行计算。

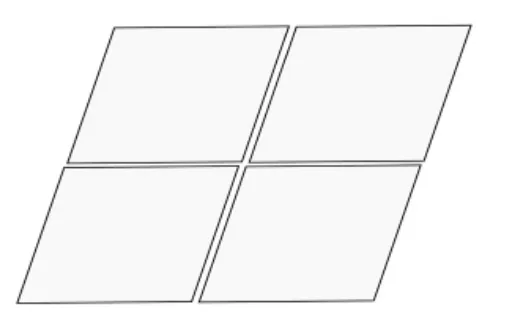
图5 20 m2定日镜示意图Fig.5 Schematic diagram of 20 m2heliostat

四相机坐标系如图 6 所示，其中 o1，o2，o3，o4分别为相机各自的坐标系。在相机采集完数据后，在后续的计算中，需要将 o1，o2，o3，o4坐标系下的数据统一到o3坐标系，即O坐标系下。

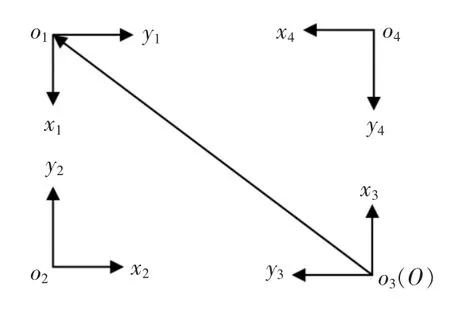
图6 四相机坐标系Fig.6 Four camera coordinate system

坐标转换矩阵定义如下：

式中：T1-3，T2-3，T4-3分别为 o1，o2，o4坐标系向 O 坐标系转换的旋转矩阵。结合点O到各坐标系原点o1，o2，o4的向量可得

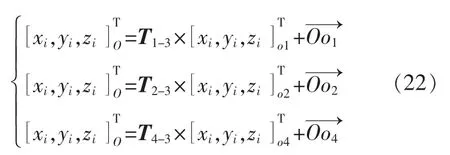
完成上述坐标转换和数据拼接，即可对数据进行反演计算，得到镜面面形数据。

3 试验验证及分析

3.1 试验装置及测量流程

搭建的试验装置如图7所示，所用试验设备主要包括投影屏幕、投影仪、待测镜面和相机。图中，待测镜面为20 m2平面镜。由于相机无法在不影响测量精度的前提下覆盖20 m2定日镜全部区域，因此采用4个相机对20 m2定日镜反射条纹数据进行采集，采用2.3节所述数据拼接算法，对四相机数据进行拼接，得到20 m2定日镜完整反射条纹数据。然后，对这些数据进行反演计算，得到20 m2定日镜面形。为避免其他光线的影响，试验在暗室条件下进行。

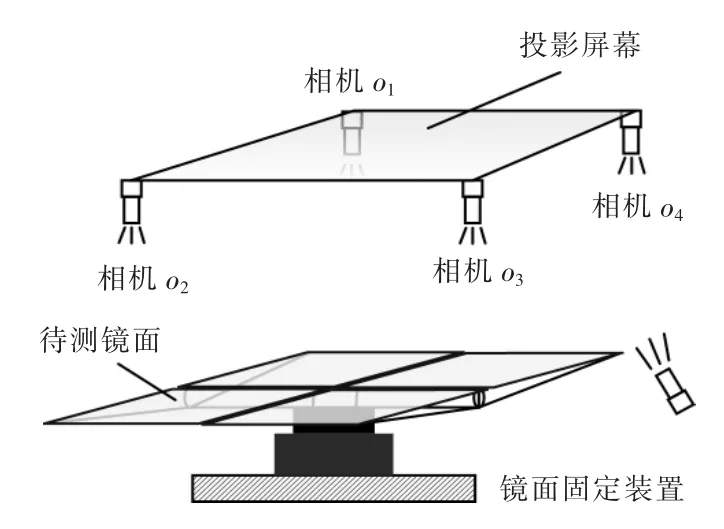
图7 系统组成的关键设备布置简图Fig.7 Schematic diagram of the key equipment layout of the system

将装配好的镜面连接座固定在试验台上，完成镜架粘贴和整机初调整后，将实验室设置为暗室环境，进行面形检测。首先，对相机进行标定[17]；主控机将调制好的条纹图像通过投影仪投射到投影屏幕上，同时主控机通过指令控制相机采集相应的图像照片；完成横向条纹测量后，主控机下发移相条纹指令直至完成整个测量；由主控机根据所采集的图像结算待测镜面面形数据。主控机工作流程如图8所示。

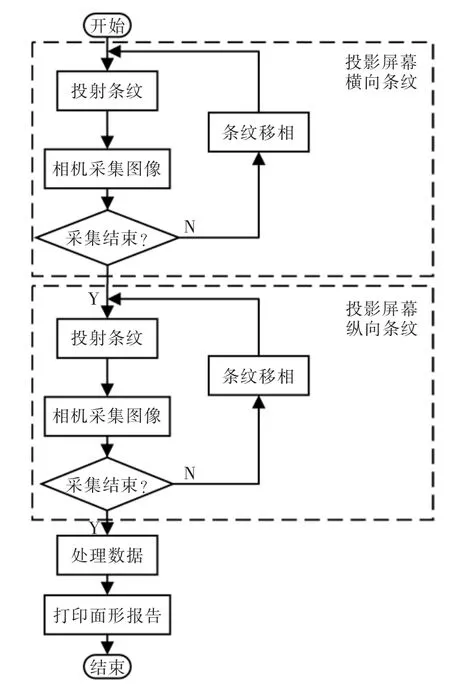
图8 检测主控制程序流程Fig.8 Flow chart of detecting main control program

3.2 试验结果及分析

尺寸为5.6 m×3.6 m即面积为20 m2定日镜条纹反射法面形测量结果如图9所示。由图可见，该定日镜中间部分高度小于边缘部分高度，二者差值约为6.5 mm，定日镜整体呈凹面形。在实际应用中，为了获得高质量定日镜光斑，提高吸热器效率，定日镜面形成凹形设计。

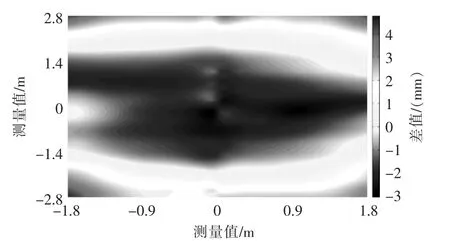
图9 20 m2定日镜条纹反射法面形测量结果Fig.9 20 m2heliostat surface measured by the fringe reflection method

20 m2定日镜测量结果与设计要求相符，说明所提出的数据拼接算法的有效性。分析表明，结合数据拼接算法，所开发的基于条纹反射的镜面面形算法可用于实际较大面积的定日镜面形测量。

4 结语

针对大面积镜面面形测量，结合数据拼接算法，开发了基于条纹反射的镜面面形检测算法，设计了镜面面形测量检测系统，采用4台相机对20 m2定日镜反射条纹数据进行采集并计算其面形数据。结果表明，该20 m2定日镜面形呈中间低、边缘高的凹面形分布，其高差为6.5 mm，符合设计要求；所开发的检测算法与面形测量系统，对大面积镜面面形的高效测量具有重要的应用价值；条纹反射法可用于较大面积的镜面面形测量，误差在允许范围内。该算法可用于实际镜面面形检测。