基于SA-KM算法和RBF神经网络的变压器故障诊断模型研究

郑文光，王爱军，王 冠，张潇文

（1.华北电力大学 电力工程系，保定 071003；2.唐山市气象局，唐山 063000；3.唐山师范学院 资源管理系，唐山 063000）

在现代电力系统对油浸式的电力设备的状态监测与故障分析方法中，油中溶解气体分析DGA技术作为重要手段之一[1]，以其对电力充油设备内部故障的诊断灵敏、有效，而得到广泛的应用。

目前，以DGA技术为基础的变压器故障诊断方法有许多，工程实际中普遍采用的有关键气体法、IEC三比值法等[2]。这些方法虽然在实际中取得了一些效果，但存在着气体比值编码缺失，编码界限过于绝对，故障方向判断片面、准确度低等缺陷。虽然，近些年来国内外学者提出了一些人工智能算法来优化这些方法，但仍然存在着一些缺点，如：BP神经网络收敛速度缓慢，容易陷入局部极小值且网络结构难以确定[3]；模糊聚类法对于大规模的样本分类效果不理想[4]；SVM同样对大规模训练样本难以适用，且在解决多种分类的问题上存在很大难度[5]；等。故在此提出了一种以DGA技术为基础，利用模拟退火思想的改进K-means（SA-KM）算法优化RBF神经网络的学习中心、宽度阈值和连接权值的初始值，来改善网络结构的方法。经过大量数据的学习训练，使用该方法建立了变压器RBF神经网络故障诊断模型。

1 基于SA的改进K-means聚类算法

模拟退火SA（simulated annealing）算法是一种启发式的随机搜索算法，其原理是模仿物理中固体物质通过先加温后冷却的方法改变粒子状态，使其内能降为最小的过程，通过重复“按规则生成新解，计算新旧目标函数差异，接受或丢弃新解”的迭代过程，得到当前最优解。采用SA算法优化的K-means聚类（KM）算法可以有效地避免目标函数因存在的大量极小值点，而使所选的中心陷入局部最优解[6]的问题，从而使算法具有良好的全局渐进收敛性和并行性，提高了算法的整体性能，增加了聚类的精确性。

SA-KM算法流程如下：

步骤1选择目标函数和参数初始化。选择样本所在的集群域中每个类别的离散度作为目标因变量，建立函数：

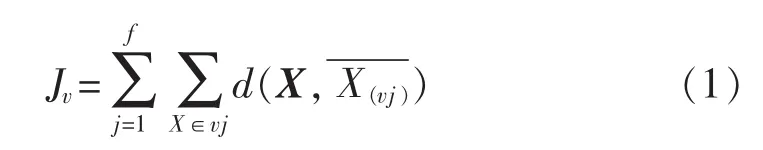
式中：聚类目标函数Jv为各种样本到对应聚类中心的距离代数和；X为样本向量；v为样本的集群聚类为 f个聚类中第 j个聚类的中心为样本到对应聚类中心的距离。其测距计算方法采用夹角余弦法，即

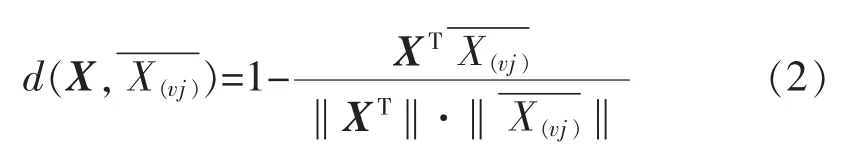
对样本进行K-means聚类，将划分结果作为初始解 v0，根据式（1）（2）计算目标函数值 Jv0。 初始化温度T0，令T0=Jv0，初始化退火速度 a和最大退火次数。

步骤2循环迭代计算。对于某一温度t，按照步骤3和步骤4进行迭代，直至最大迭代次数跳到步骤5。

步骤3生成模型扰动。更改一个样本的类别，产生对当前群集聚类的一个随机扰动，生成新的群集聚类v′，并计算新的目标函数值Jv′。

步骤4选择存优并取得新解。确定新的目标函数值Jv′是否为最优目标函数值，是否将集群聚类v′保留为最优集群聚类，并将Jv′作为最优目标函数值；否则按式（3）计算新的目标函数值与当前目标函数值的差值，判断其差值是否小于0，是则接受新解，即将新解作为当前解，否则根据Metropolis准则，以式（3）所得概率接受新解。

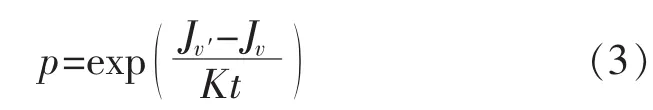
式中：K为常数；t为当前温度。

步骤5按条件结束算法。判断算法循环是否达到最大退火次数，是则结束算法，输出最优聚类划分；否则根据退火公式对温度进行退火寻优，回到步骤2继续迭代。退火公式为

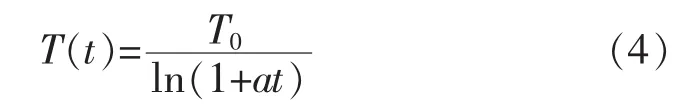
式中：T0为初始温度；a为退火速度。a为可调参数，可以改变退火过程曲线的形态，使其在高温区降落得快，低温区降落得稍慢，以便于在低温区寻得最优解，提高收敛的精确度。

2 RBF神经网络

RBF神经网络是一种性能优异的前向网络，具有最佳逼近性能[7]。其拓扑结构是一种三层前馈网络，如图1所示。其基本思想是将输入向量X=经过输入层，传递至用RBF作为隐单元的“基”的隐含层空间，经过空间映射变换后到达作为输入模式响应的输出层[8]，得到输出向量Y=

其中，隐含层神经元的核函数Φj为高斯函数：

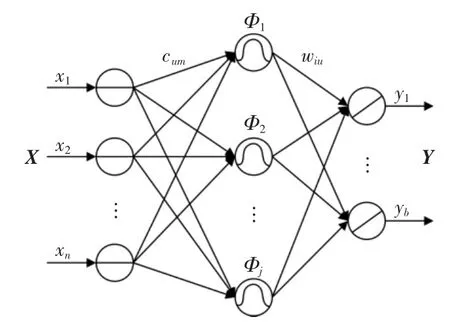
图1 RBF神经网络拓扑结构Fig.1 Topological structure of RBF neural network

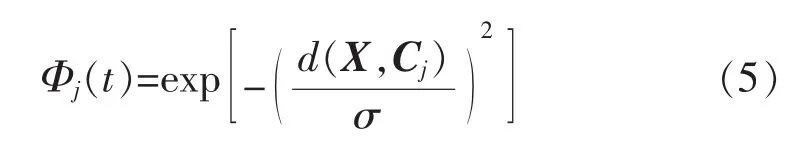
式中：d（X，Cj）为网络传递函数的输入向量X和学习中心向量Cj之间的角度余弦；σ为宽度阈值。σ的求解方法为

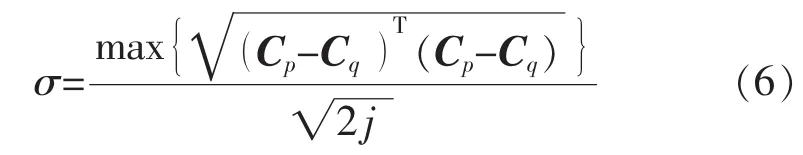
式中：Cp和Cq分别为第p，q个学习中心向量。

3 变压器故障诊断模型的建立

对于RBF神经网络的学习算法，其关键在于相应参数初始值的确定，合理恰当地选择初值，不仅可以大大加快算法收敛速度，而且可以有效避免复杂函数陷入局部极小值，优化网络结构，增强网络聚类的精确性。故在此使用SA-KM算法优化RBF神经网络相关参数的初始值，从而建立相应的变压器故障诊断模型。模型的建立过程如下：

步骤1建立样本及中心数据库。将变压器产生故障时的m组DGA数据组建样本库，每组数据 均 为 以 H2，CH4，C2H4，C2H6，C2H2和 总 烃 的 含 量体积分数 （10-6）为特征值的特征向量，即Xs=其中 s=1，2，…，m，确定聚类类别数量b，同时初始化样本数据与网络中心。

步骤2确定RBF神经网络的学习中心和宽度阈值的初值。根据分类需求，确定RBF神经网学习中心数量为j。将样本库中各组故障气体DGA数据作为样本向量，利用SA-KM算法计算出各个初始学习中心向量其中 k=1，2，…，j；初始学习中心矩阵由式（6）得出对应的初始宽度阈值σ0。

步骤3确定RBF神经网络的连接权值的初值。以变压器故障气体DGA数据作为输入向量，按照式（5）经过RBF网络隐含层传递函数变换后，得到隐含层的初始输出向量 Gs0=［gs1，gs2，…，gsj］T，使用最小二乘法计算，获得网络中隐含层至输出层之间的连接权值wiu为

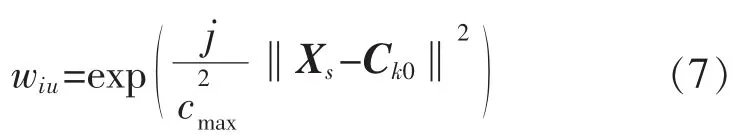
其中

i=1，2，…，b；u=1，2，…，j

以连接权值向量 Wiu=［wi1，wi2，…，wij］T（其中 i=1，2，…，b）为输入向量，将 SA-KM 算法计算出的聚类的中心矩阵W0作为连接权值的初始值。

步骤4确定RBF神经网络的目标输出向量。以中心向量作为输入，将各参数初始值代入RBF神经网络，得到网络的目标输出向量O为

步骤5参数迭代计算。RBF神经网络参数的训练方法采取梯度下降法，学习中心cun，宽度阈值σun和连接权值wiu分别按式（9）代入变量因子S，循环迭代至最佳值：

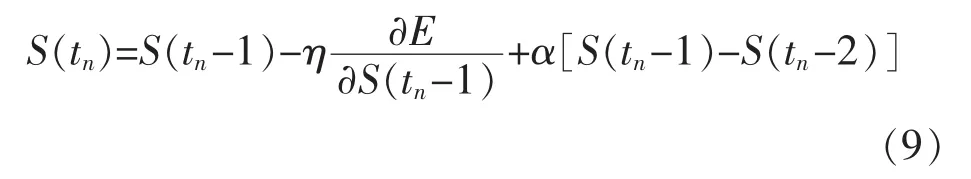
其中

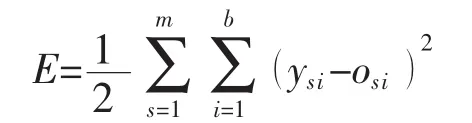
式中：tn为迭代次数；η为学习因子；α为学习速率；E为RBF神经网络评价函数。

4 实例分析

4.1 建立变压器故障模型

在此选择147组变压器故障气体DGA数据进行分析，其中112组数据用于样品训练来建立网络模型，剩余35组数据用于对网络模型进行测试。将变压器的故障类型划分为7类，编号及名称是：①低温过热；②中温过热；③高温过热；④低能放电；⑤高能放电；⑥电弧放电；⑦过热并伴随放电。各类故障各选用21组数据。

经过多次仿真试验与分析，最终确定以6-7-7的3层RBF神经网络结构为基本框架，将变压器油中6种溶解的特征气体数据作为RBF神经网络的输入，使用SA-KM算法计算神经网络参数初值。其中，取网络学习中心数为7，取最大迭代次数为180，取最大退火次数为180，退火速度a=0.9，2次退火结束后目标函数值分别为Jv1=0.2374，Jv2=0.1273。经过计算，得到学习中心初始向量C0，始宽度阈值σ0，初始连接权值矩阵W0和目标输出矩阵O（见表1）为

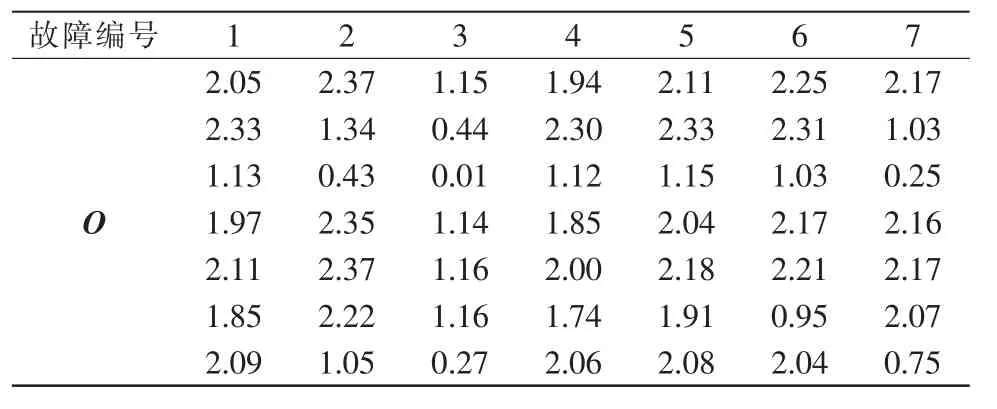
表1 故障类型对应目标输出向量Tab.1 Target output vectors corresponding to fault types

以上述参数初值按照式 （9）进行循环迭代计算，建立RBF神经网络分类模型。其中迭代次数tn=150；学习因子 η=0.9；学习速率 α=0.1。

4.2 仿真试验

将所建立的故障诊断模型进行封装，使用MatLab软件设计基于SA-KM-RBF算法的变压器故障诊断模型的GUI界面，如图2所示。

输入需要诊断故障的变压器各气体含量，对模型进行仿真测试，各种故障类型均使用5组测试数据进行仿真诊断。将该模型的仿真测试结果，分别与仅采用RBF神经网络的变压器故障诊断方法和目前工程上常常采用的IEC三比值变压器故障诊断方法，进行比较分析。各种方法的故障诊断结果、故障分类误差和分类结果比较分别如图3和图4所示，测试样本分类结果对比见表2。

图2 变压器故障诊断模型GUI界面Fig.2 GUI interface of transformer fault diagnosis model

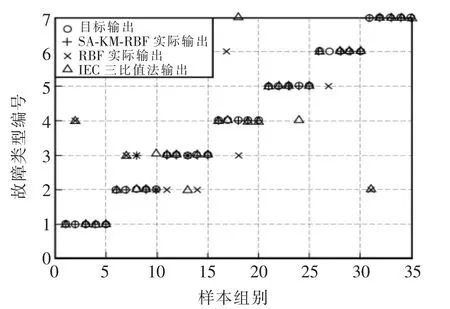
图3 测试样本分类结果Fig.3 Test sample classification results

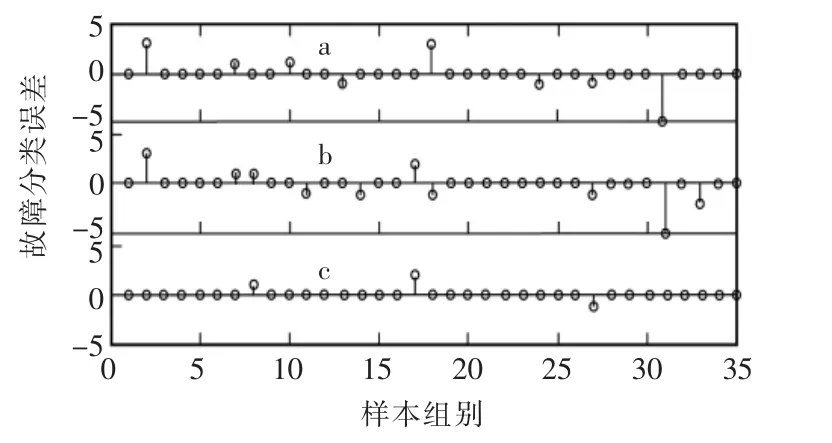
图4 测试样本误差Fig.4 Test sample error

表2 测试样本分类结果对比Tab.2 Classification results and comparison of test samples

结果表明，采用SA-KM算法优化的RBF神经网络的变压器故障模型诊断正确率高达91.43%，远高于采用RBF神经网络进行变压器故障诊断的71.43%的正确率和IEC三比值法进行变压器故障诊断的77.14%的正确率；与使用诸如GA-BP算法、BPNN算法等其它智能算法优化的变压器故障模型相比，SA-KMRBF优化算法也具有更高的正确率[9-10]。

5 结语

本文提出了一种SA-KM-RBF优化算法的变压器故障诊断模型，通过SA-KM算法优化RBF神经网络的初始参数，从而改善了变压器故障诊断模型的结构，提高了变压器故障诊断的准确性。该模型能很好地适用于大容量故障样品多分类的难题，且结构简洁，全局收敛性强，分类精度高，非常适合对变压器的选型设计、状态监测和故障诊断分析。经过仿真测试验证，该方法的正确率高达91.43%，在变压器故障诊断过程中拥有良好的性能，具有出色的实用性和有效性，非常值得在推广与应用。