基于演化博弈的矿区生态补偿激励约束机制研究

王 莹，彭秀丽

（中南林业科技大学 商学院，湖南 长沙 410000）

我国资产资源丰富，但开采利用规模已经触及环境质量承载上限，地貌、植被、水体都受到较大程度的破坏，即破坏了矿产资源所在地生态环境的负外部性。虽然，我国制定了有关生态环境的相关保护法[1-2]，但是由于这种负外部性带来的影响并没有得到及时有效的消解，因此，有必要探索厘清矿产资源生态补偿的内在博弈态势和动态演化机理，建立明晰的补偿分担制度。

在生态补偿的过程中，生态补偿群体利益关系错综复杂，而矿产资源开采企业和政府部门作为最重要的两个生态补偿关系，其利益冲突则是双方利益激化的矛盾所在，双方均有自身可选择性，因此，矿产资源开采企业和政府部门之间的博弈关系具有动态性。演化博弈经过多方学者的推敲应用，在生态补偿演化中发挥着不容忽视的作用，其中以流域生态补偿应用最广。流域生态补偿实际就是通过下游对上游进行生态补偿以达到均衡生态补偿关系内各个主体的利益关系的效果[3-6]。相比流域生态补偿而言，矿产资源生态补偿利益方更加错综复杂，而矿产资源开采企业和政府部门作为最重要的两个生态补偿方，平衡双方之间的利益关系也显得尤为重要[7-9]。因此，建立一套健全的生态补偿机制不仅可以达到保护当地生态环境的效果，还可以均衡各利益方之间的经济利益冲突[10]。

矿产资源所在地丰富的矿产资源在很大程度上带动了当地的经济发展。但是当地长期以来对矿产资源的大量开采已对当地的生态环境造成了严重破坏，虽然矿产资源所在地均在保护当地生态环境做了大量工作并取得了一定的效果，但是总体上来看，仍未从根本上解决矿产资源所在地生态环境的保护治理问题。矿产资源开发过程中缺乏资金保障，保护利益关系不均衡，矿区居民生活环境日益恶化等问题日渐突出。政府和矿产资源开采企业作为两个重要主体，一方面企业开采矿产资源必然会对当地生态环境造成破坏，另一方面政府在是否同意企业开采矿产资源有环境保护压力。处于重压力生态保护下的地方政府部门和利益驱使下的企业矛盾越来越大。因此，构建生态补偿机制来协调地方政府部门和矿产资源开采企业之间的矛盾，缓解当地的生态环境已是迫在眉睫。

为此，本研究通过构建矿区生态补偿演化博弈模型，分析矿产资源开采过程中的地方政府部门和企业之间的利益均衡策略，并通过MATLAB对引入激励约束机制的生态补偿演化博弈模型进行仿真分析，得出最优生态保护策略（政府监管，企业补偿）状态。

一、矿区生态补偿演化博弈模型的构建

（一）矿区情景设定

为了简化分析，本研究将矿产资源所在地的矿产资源开发过程中的利益主体概括为地方政府部门和矿产资源开采企业。

矿产资源开采企业作为矿产资源开发和生态补偿的主体，通过开采矿产资源，来获取自身利益，开采量与其自身获利成正比。同时，矿产资源开采企业处于追求利润最大化的本能不一定会对损坏的生态环境进行生态补偿。因此，矿产资源开采企业可选择“主动补偿”和“不主动补偿”。作为矿产资源的所有者和管理者的地方政府部门，在保证当地经济水平平稳发展的同时，还要保证当地生态环境的绿色发展。这种双重角色要求政府制定的关于环保、可持续发展的规划目标应充分考虑社会的共同利益，从而提高了政府的形象，创造良好的社会环境。因此，地方政府部门在矿产资源开采过程中可选择的策略为“监管”或“不监管”。但是追求自身利益的最大化是两者之间的共性，而“补偿—监管”策略则是生态文明建设所期盼的最优策略。

（二）矿区生态补偿演化博弈支付矩阵

在矿区生态补偿演化博弈模型中，假定为：R1：政府自身的初始收益；R2：政府监管支出；R3：政府监管收益。U1：企业自身的初始收益；U2：企业补偿成本指出；U3：企业补偿后的经济效益。A：政府在企业补偿后给的生态补偿额。

于是，地方政府部门和矿产资源开采企业的生态补偿收益矩阵如表1所示：

表1 地方政府部门和矿产资源开采企业的生态补偿 收益矩阵

假设地方政府部门采取监管策略的概率比例为X，矿产资源开采企业采取补偿策略的概率比例为Y。则1-X为地方政府部门采取不监管策略的概率比例，1-Y为矿产资源开采企业采取不补偿策略的概率比例。X=1 表示地方政府部门全部采取监管策略，Y=1 表示矿产资源开采企业全部采取补偿策略。反之，X=0 表示地方政府部门全部选择不监管策略，Y=0 表示矿产资源开采企业全部选择不补偿策略。

由此，地方政府部门选择监管策略的期望收益为U11，选择不监管的期望收益为U12，则地方政府部门的平均收益为U1：

矿产资源开采企业选择进行生态补偿策略的期望收益为U21，选择不进行生态补偿的期望收益为U22，则矿产资源开采企业的平均收益为U2：

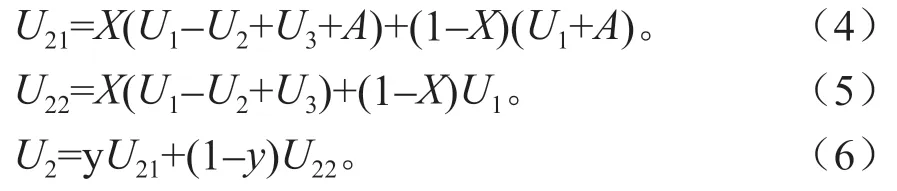
根据动态复制方程，地方政府部门和矿产资源开采企业的动态复制方程分别为：

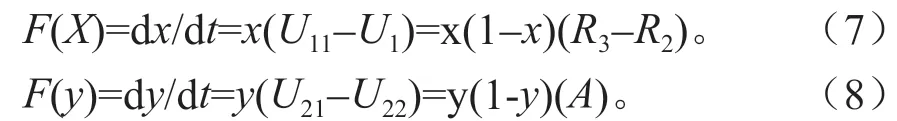
上面的公式（7）和（8）构成的博弈动态复制方程系统。在一般情况下，动态博弈系统的进化稳定策略可以通过分析当地的平衡点的稳定性进行研究。据弗里德曼提出的方法[11]，此时平衡点的稳定分析可由Jacobi 矩阵分析可得，因此，公式（7）和（8）的Jacobi 矩阵对应的行列式和其迹为：

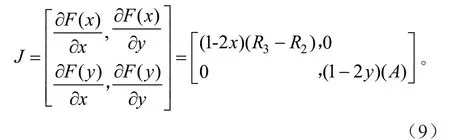
行列式为：

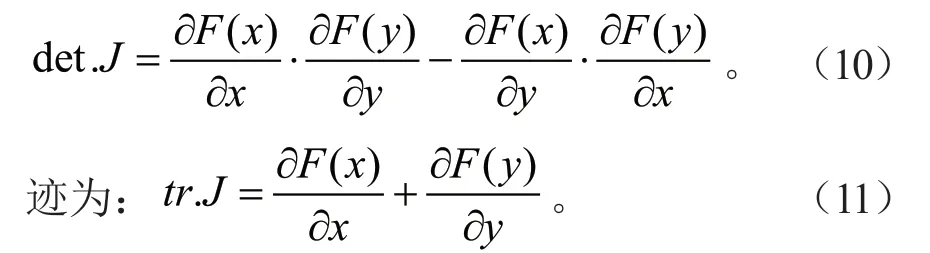
由Friedman 的思想可知，如若策略（x，y）为稳定均衡策略，则应该有相应的行列式det.J＞0，迹tr.J＜0。同时，社会所期望的最优策略（监管—补偿）为稳定策略，即（x=1，y=1），因此，代入式（10）和（11）之中，应该为：

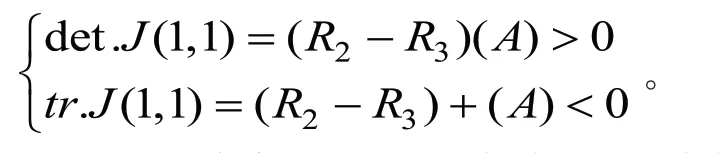
由于地方政府部门对矿产资源开采企业的补贴A＞0，根据行列式det.J＞0 有R2-R3＞0，但是这与tr.J＜0 相矛盾，所以，在此情况下，动态方程式无解。因此，可以推断出，在一个没有外部干预的情况下，单靠市场调节无法实现整个社会所期望的最优稳定策略（监管—补偿）。基于此，在矿产资源生态补偿过程中，需要引进中央政府部门干预，通过中央政府激励约束机制使得矿产资源生态补偿过程中贴近演化最优策略。

（三）引入激励约束机制后的矿区生态补偿演化博弈模型

由于矿产资源开采企业与地方政府部门之间存在主体对等性，尽管地方政府部门更期望矿产资源开采企业可以主动对矿区进行生态补偿策略，但是矿产资源开采企业自身趋于追求自身利益最大化的前提下，很可能选择不补偿，此时就难以达到（监管—补偿）的最优策略。基于此，现在之前的模型中引入激励约束机制。

如果地方政府部门选择监管策略，而矿产资源开采企业并未进行生态补偿，则中央政府部门对矿产资源开采企业进行经济处罚；相反，如果是矿产资源开开采企业选择进行生态补偿，而地方政府并未选择监管策略，然后中央政府对地方政府的经济处罚。因此，将经济惩罚设置为变量F引入到演化博弈中，此时就形成了新的地方政府部门和矿产资源开采企业的收益矩阵（表2）。

表2 引入经济惩罚后的地方政府部门和矿产资源开采 企业收益矩阵

此时，地方政府部门选择监管策略的期望收益为U11′，选择不监管的期望收益为U12′，则地方政府的平均收益为U1′：

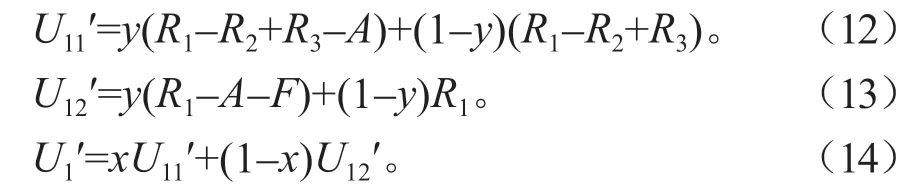
矿产资源开采企业选择进行生态补偿的期望收益为U21′，选择不进行生态补偿的期望收益为U22′，则矿产资源开采企业的平均收益为U2′：

于是，地方政府采取动态复制的策略为：

矿产资源开采企业采取动态复制的策略为：

在各自的动态复制过程中，均出现了博弈的对手方y与x，这意味着，由于中央政府激励约束机制的介入，对不合作的个体进行经济处罚，使得地方政府部门和矿产资源开采企业监管与补偿策略的比例发生变化，如果处罚的金额到达一定程度，将有可能会引导地方政府部门和矿产资源开采企业的选择朝着社会期望的策略演变。下面分别对地方政府部门和矿产资源开采企业的演化路径及稳定策略进行分析：

1.地方政府部门的演化路径及策略

对于式（12）求关于x的一阶导有：

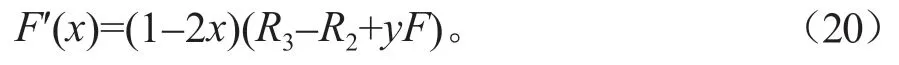
令上式F(x)=0，根据方程可得，x*=1 和x*=0 两个可能的稳定动态点。基于此，有以下三种情况：

1）当y*=(R2-R3)/F时，总有F(x)=0 成立，此时所有的x 都是处于稳定状态。即当矿产资源开采企业选择以y*=(R2-R3)/F的水平状态选择生态补偿策略的时候，地方政府部门选择监管或者不监管策略的收益并没有区别，因此对于所有的x都是地方政府部门的稳定状态。

2）当y＞y*=(R2-R3)/F时，x*=1 和x*=0 两个可能的稳定动态点。此时由于F′(1)＜0，所以x*=1 是稳定演化策略。即当矿产资源开采企业选择以高于(R2-R3)/F的水平状态进行生态补偿策略时，地方政府部门逐渐地由不监管策略转向监管策略。因此此时监管策略是地方政府部门的演化稳定策略。

3）当y＜y*=(R2-R3)/F时，x*=1 和x*=0 两个可能的稳定动态点。此时由于F′(0)＜0，所以x*=0 是稳定演化策略。即当矿产资源开采企业以低于(R2-R3)/F的水平状态进行生态补偿策略时，地方政府部门逐渐地由监管策略转向不监管策略。因此此时不监管策略是地方政府的演化稳定策略。

2.矿产资源开采企业的演化路径及策略

对于式（13）求关于x的一阶导有：

令上式F(y)=0，根据方程可得，y*=1 和y*=0 两个可能的稳定动态点。基于此，有以下三种情况：

1）当x*=-(A/F)时，总有F(y)=0 成立，此时对于所有的y 都处于稳定状态。即当地方政府部门以-(A/F)的水平状态选择监管策略时，对于矿产资源开采企业选择进行生态补偿行为或者不进行生态补偿行为的收益并没有区别。所以对于所有的y都是矿产资源开采企业的稳定状态。

2）当x＞x*=-(A/F) 时，y*=1 和y*=0 是 两个可能的稳定动态点。此时由于F′(1)＜0，所以y*=1 是稳定演化策略。即当地方政府部门选择以高于-(A/F)的水平状态监管策略时，矿产资源开采企业选择逐渐地由不进行生态补偿策略转向进行生态补偿策略。因此此时选择生态补偿策略是矿产资源开采企业的演化稳定策略。

3）当x＜x*=-(A/F) 时，y*=1 和y*=0 是 两个可能的稳定动态点。此时由于F′(0)＜0，所以y*=0 是稳定演化策略。即当地方政府部门选择以低于-(A/F)的水平状态监管策略时，矿产资源开采企业选择逐渐地进行生态补偿策略转向不进行生态补偿策略。因此此时选择不进行生态补偿策略是矿产资源开采企业的演化稳定策略。

与此同时，上述式中的稳定动态点介（0,1）之间，由此推断出，y*=(R2-R3)/F和x*=-(A/F)也介于（0,1）之间。因此可得：

因 此，0 ≤(-A) ≤F，0 ≤R2-R3≤F，R3≤R2。由此可知：

1）对于不合作方的罚金应该大于矿产资源开采企业多付出的生态补偿额和政府部门的监管成本；

2）地方政府部门不监管的初始收益应该小于地方政府监管后的收益。

在上述约束条件之下，对式（18）和（19）进行Jacobi 矩阵分析：

基于式（24），将四种策略带入矩阵中进行分析，并求出相应的行列式与迹，如表3所示：

表3 系统雅可比矩阵

将约束条件式（22）和式（23）带入表3系统雅可比矩阵中，进行局部稳定性分析，如图4所示：

表4 均衡点的局部稳定性分析结果

由表4可知，此时的稳定点即演化稳定策略为（0,0）和（1,1）。不稳定点为（1,0）和（0,1），（x*，y*）为鞍点。此时，地方政府部门和矿产资源开采企业之间的演化博弈动态过程如图一所示：

图1 复制动态相位

图1用动态图描述了在中央政府激励约束机制的介入下，地方政府部门与矿从资源开采企业之间的演化博弈动态行为。由不稳定点（0,1）和（1,0）以及鞍点（x*，y*）连起来的直线将整个方块儿区域划分为H、M两块，它是系统在（0,0）和（1,1）两个状态下的演化分界线。如果最初的状态选择在H区域内，则系统会倾向于（0,0）不稳定点收敛，即此时地方政府部门和矿产资源开采企业的选择策略是（不监管，不补偿）。相反，如果最初的状态选择在M区域内，则系统会倾向于（1,1）不稳定点收敛，即此时地方政府部门和矿产资源开采企业的选择策略是（监管，补偿），这样一来，整体就会更接近于社会期望的最稳定的策略。

区域H、M相对面积比例的大小则是通过对鞍点（x*，y*）参数的调整来改变，这样会改变系统不稳定点收敛的概率也会随之改变，最终使得系统朝着不同方向所演变。

综上所述，首先相对于之前在没有中央政府激励约束机制下的介入，即对不合作方没有任何经济处罚时，在引入激励约束机制后明显能够使得系统整体朝着社会所期望的（监管、补偿）策略方向移动，而前者则不可能做到；其次，尽管引入了激励约束机制，但是由于地方政府部门和矿产资源开采企业之间的博弈行为的最终动态演化结果取决于鞍点的位置和初始状态点的选择区域，所以此时也有可能走向（不监管、不补偿）的策略选择方向。

最后，在鞍点的参数选择中，有F、A、R2、R3四个参数，它们的大小决定了鞍点的位置，进一步决定了H、M区域的大小，从而对整个系统的演化造成影响。而经济处罚F 是能够具体决定中央政府部门经济处罚金额大小的参数变量，所以，根据稳定策略det.J（1,1）＞0，tr.J（1，1）＜0 可以得到一下关系式：

由此得出：

所以，F的范围应该小于C 与R2-R3中的最小值；另一方面，在鞍点（x*，y*）中，为了让系统朝着社会所期望的点移动，因此，初始点的位置应该尽可能地落入M区域内，这也就意味着x*→0，y*→0，所以对于分母F而言，越大的罚金就意味着M的区域增大，即较大的经济处罚能够对不合作方起到一个约束作用，从而引导整个系统朝着社会期望的方向所移动。

三、数据仿真分析

基于以上演化博弈，假设地方政府监管成本的机会成本为100 个单位值，通过监管措施所获得的生态价值为50 个单位值，初始地方政府部门采取生态补偿支付的比例0.4，矿产资源开采部门采取生态补偿支付的比例为0.6。同时，将双方的学习率设为0.3。仿真情景如图2所示：

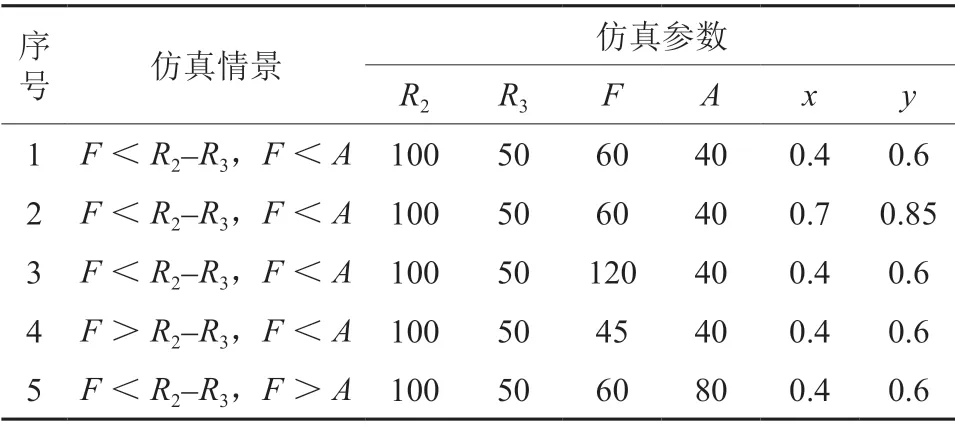
表2 仿真情景

采用MATLAB 仿真技术进行分析，结果如图2所示（图2-6 的纵坐标均表示生态补偿横向转移支付的比例，横坐标均表示仿真过程中个体的学习速度）。

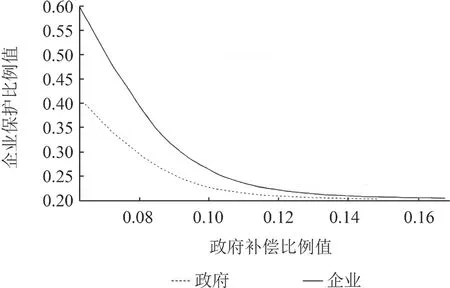
图2 演化路径

地方政府部门和矿产资源开采企业的演化途径图4是仿真设置中地方政府部门和矿产资源开采企业初始情况的演化博弈。通过计算可知，在这种情况下，演化博弈的鞍点值为：

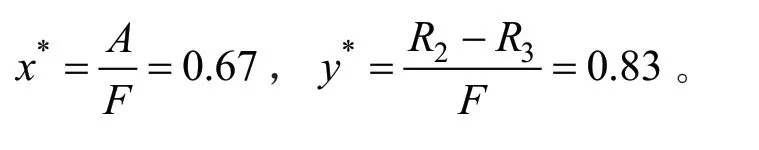
图3 演化路径

由此可见，当地方政府部门和矿产资源开采企业的生态补偿意识不够强烈时，仅仅只有比例为40%的地方政府部门愿意采取监管措施，60%的矿产资源开采企业愿意主动采取生态补偿措施，博弈结果最终将走向x*→0，y*→0 的矿产资源困境。因此，当经济惩罚的力度不够大时，只有当地方政府部门和矿产资源开采企业的生态意识都足够强大的时候，博弈最终才能走向社会期望（监管，补偿）的局面，如图4所示。当中央政府的经济惩罚力度足够大的时候，在仿真技术图中表现为经济惩罚变量远远超过生态补偿补贴A 时，此时的鞍点值为：

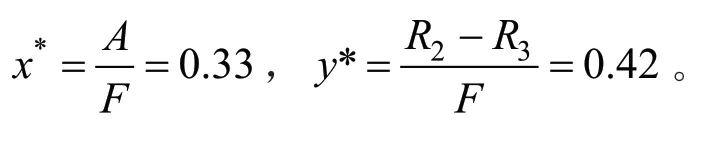
图4 演化路径

此时相对于仿真情形一（图2），博弈结果更容易走向社会期望（监管，补偿）策略。而当经济惩罚变量F＜R2-R3的时候，此时对于地方政府部门来说，不进行对矿产资源生态补偿的监管将会获得更多的经济收益，因此，惩罚最终将走向地方政府部门监管、矿区资源开采企业不补偿的困境。相反，当矿产资源开采企业所付出的生态补偿成本超过中央政府对于不合作方的经济处罚时，大部分的矿产资源开采企业将会选择接受中央政府的经济处罚，此时的博弈结果就走向了“公地悲剧”，如图5所示。

四、结论及建议

本研究从矿产资源开采的现实情况出发，基于演化博弈，采用动态复制方程式，推算出生态补偿最佳补偿方式及均衡点。

第一，基于矿产资源所在地的矿产资源开采生态补偿实际情况，矿区生态补偿在基于多元化、市场化生态补偿的基础上，应引入政府激励约束机制，通过政府的强干预去均衡、督促各方利益主体主动进行生态补偿。由于市场当方面调节具有利益驱动性，企业很可能在权衡利弊后而选择不补偿，此时政府强行进行干预，采取激励约束机制，应满足条件：0 ≤y*=(R2-R3)/F≤1 和0 ≤x*=-(A/F)≤1，寻求达到利益均衡和最佳利益状态。

图5 演化路径

第二，本研究利用MATLAB 动态仿真技术图对矿产资源进行仿真模拟数据分析，推算出政府和企业的生态补偿最佳均衡点分别是0.33 和0.42。在上级政府对违约方进行高额惩罚的状态下，企业和当地政府都会更加积极主动的进行生态补偿，达到（企业补偿，政府监管）的最优状态。

因此，综上所述，中央政府在矿产资源开采过程中应采取激励约束机制，对地方政府部门和矿产资源开采企业采取不同的行政强制手段。

首先，对于地方政府政府部门，应该在现有“按照绩效奖罚”的基础上，建立“复合式”财政转移支付，督促地方政府对矿产资源开采进行监管，并降低地方政府监管成本，提高监管收益，建立健全监管机制和引导机制。

其次，对于矿产资源开采企业而言，应该通过强制性监管，在强制性惩罚的基础上建立对矿区进行生态补偿机制，并积极引入市场机制，加强生态系统价值损益评价，使环境绩效向经济绩效转换；企业应增强自身的社会责任感，积极主动的对矿区进行生态补偿。

最后，应该建立健全矿产资源开发的生态保护及生态补偿的法律制度建设，明确和强化中央政府激励约束机制的监管作用，提高对地方政府部门以及矿产资源开采企业的约束力和权威性。加大生态环境保护的宣传，并加强公众的环保意识，加强公众的环保意识，进一步督促监管地方政府部门的监管作用和矿产资源开采企业的生态补偿行为，从源头上解决矿产资源所在地的生态环境保护问题。