基于图论的上海轨道交通站点客流等级预测研究

于 莉, 刘志钢, 石志峰, 陈颖雪, 张香明

(上海工程技术大学 城市轨道交通学院， 上海 201620 )

0 引 言

随着中国大中型城市轨道交通建设快速发展，轨道交通线网的拓扑结构越来越复杂。对轨道交通车站的特性进行分类，可以有目的地了解不同种类站点之间的差异，科学合理的站点分级体系能够为地铁车站人员配置、资源分配及管理提供决策依据。应用图论的方法可以将城市轨道交通的线网用数学模型方法进行描述，不仅可以区别于传统的以车站性质和周边用地性质来进行站点等级划分，又可以在复杂的线网中准确地提取线网自身的规律和特点。

由于城市轨道交通线网的复杂性，国内外学者主要研究图论中的点、线以及整体性指标对线网结构改变后的评价方法及结果。慈立坤等人[1]使用图论的方法研究上海轨道交通运营网络的特性并建立了线网可靠性评价模型，论证了当网络节点破坏不同出行路径影响大小不同。四兵锋等人[2]从图论的角度出发，构建了多层次的交通系统网络结构并进行描述，获取乘客对于网络进行的差异性选择并建立以乘客出行需求为基础的广义费用模型和路阻函数。在站点分级的研究中， WEI等人[3]选取客流量、位置和客运服务指标对车站进行打分，并提出客流量等级公式；余丽洁等人[4]在确定影响轨交站点属性因素参数的基础上，以西安地铁2号线为例，采用多种聚类算法对站点分类效果进行评述。陈扶崑等人[5]选取行车组织方案、车站客运服务、客流量和地理位置四个指标，应用定量分析方法，建立城市轨道交通车站等级划分体系标准。

本文从图论的角度出发，针对新线开通初期，引入站点客流等级预测方法，通过车站图论等级与客流等级的相关性分析，两者成强正相关，建立相应的预测标准。

1 上海轨道交通线网模型建立

图论是专门用于研究图的一个数学分支，提供了描述网络的语言和研究的平台，通过对图的研究可以得到具体的实际网络的相关拓扑性质[6]。城市轨道交通线网是由各个车站和各条线路组成的拓扑网络，可以抽象为由点、线组成的基本图形，车站作为一个点，两站点间的线路作为图形中的边。用图论的方法表示城市轨道交通线网可以清晰地描绘出线网内部的各种关联关系，通过计算机准确地刻画出线网模型并完成进一步的定量处理。城市轨道交通线网图可表示为：

G=(V(G),E(G),φG).

(1)

其中，G表示城市轨道交通线网图；V(G)表示车站集；E(G)表示两站间线路集；φG表示关联函数。E(G)中的每条边都有V(G)中的一对点与之相对应。在本文中将轨道交通线网视为无向图，可使图G的每条边对应于G无序顶点对。

由于Space L方法构建的模型简单却能够很好地重现线网的实际拓扑结构，因此本文采用Space L方法构建线网模型，如图1所示。

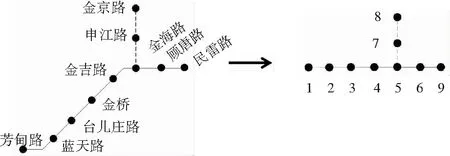
图1 Space L模型实例

为了获得图论角度下上海轨道交通线网的一般拓扑结构规律及特征，在建模时对线网进行了简化：首先，不考虑实际运营中站点的区位以及距离等信息，假定各站之间的距离为1；其次共线区段合并为一条线路(主要为3、4号线的宝山路站-宜山路站及2、10号线的虹桥火车站至虹桥2号航站楼)；最后，地铁线网拓扑结构图为无向无权图(不区分上下行)。

应用space-L方法建立上海轨道交通线网拓扑模型，如图2所示。

图2 上海轨道交通线网拓扑结构图

Fig. 2 Topology of Shanghai rail transit network

2 轨道交通站点重要度评价指标确定

目前，复杂网络中最主要的统计指标有：度值、接近中心性以及介数值[7]等。这些指标从不同的角度对网络结构进行了描述，并且较为全面地反映线网内部的特性。

对上海轨道交通线网中的站点评价指标进行计算，由于大型城市的中心站点本身影响力较大，会对距离较近的周边站点存在辐射影响，造成同类型站点间的重要度差异。因此，综合地理位置和用地信息等选取了上海市4个城市中心车站，包括位于城市主中心的人民广场站和3个位于城市副中心的世纪大道站、中山公园站以及徐家汇站。在不考虑换乘便捷性的情况下，利用Dijkstra算法将各个车站至城市中心站的最短距离求解出来，并将其作为一项重要度指标放入模型中，部分站点指标数值见表1。

表1 站点指标数值表(部分)

3 基于K-means的车站重要度等级聚类及特征分析

由于地铁车站分布于全网，其地理区位不同导致服务客流量差异较大，聚类变量的选取需结合图论中的指标来反映节点空间结构特性，站点距离城市中心站点及城市副中心站点的最短路距离替代土地利用指标，反映站点在实际线网拓扑结构中的重要度。本文引入K-means聚类算法模型[8]，建立综合评价指标的车站等级划分方法。

上海轨道交通站点数量较多，为了使站点重要度等级更加符合实际的情况，需对部分首末站、大型对外交通枢纽站点指标参数进行适当的提高，以保证站点分级的合理性和有效性。考虑可以更加明确区分各类型车站的特征，选取参数k为10进行聚类，经过多次迭代得到最优的车站等级聚类结果。代表车站聚类结果见表2。

对304个车站的聚类结果进行汇总，根据各类型车站的特征得到轨道交通站点分类结果共10类，具体内容见表3。

表2 上海轨道交通代表车站聚类结果(部分)

表3 上海轨道交通车站重要度等级

4 站点客流等级预测实例研究

为了将复杂的预测方法进行简化，不再仅仅关注站点客流的具体数值，而是研究站点相关客流等级。考虑利用站点在图论中的重要度来推算相应的站点客流等级，从而在新线开通初期可以对各个站点客流情况有个较为简便准确的获取方式。对此拟展开研究阐述如下。

4.1 站点进出站客流分布及分类

由于是根据所建的站点图论重要度等级来进行预测，因此得到的预测结果也应是相应的客流等级。针对各个站点的实际客流量进行站点客流等级的划分，绘制各个站点的历史某天的进站客流量数值图，如图3所示，从实际数据量上可知上海地铁站点的进出站量最小值约在1 400人/天，而最大值在11万人/天，进出站量在3万人/天以下的站点数占了总数的约83%，由此可见客流数据的范围较大且各数据级的分布十分不均衡。

图3 线网各站点进站客流量数值分布图

Fig. 3 Numerical distribution of inbound passenger flow at each station

为了保证客流等级的分类能够较为准确地反映出站点的实际客流量区间，所以在进行客流等级分类时舍弃均匀分配的方法。针对前六等级的站点以较小的数据间隔5 000人次进行划分，而后四级则以较大的数据间隔进行划分。由于在该种划分方式下的各客流等级实际间距较大，所以能够在一定范围内忽略站点客流的自然增长情况。具体分类标准见表4。

表4 客流等级具体分类标准

利用实际进站客流数据、分类好的各个站点的客流等级数据分别与图论重要度等级进行相关性分析，可以进一步证实该预测方法的准确性。

4.2 相关性分析

结合本次数据的特征，选用Spearman相关系数进行分析。根据各个站点的实际进出站量以及上文所构筑的站点图论重要度等级指标来对数据进行初步的相关性分析，可知其相关系数均大于0.7，为强正相关关系。

同时利用SPSS对2种划分方法下的分类结果进行进一步的Spearman相关性分析，研究可得在图论角度及客流角度下的部分站点的划分结果比较见表5。

表5 图论角度及客流角度下的站点分类结果表(部分)

经计算得出相关系数为0.733，同样为强正相关，验证说明，随着图论等级的上升，客流等级也会相应的提高，因此能够根据新线开通前后站点重要度的变化来反映实际客流等级的变化，从而利用图论中的分类等级来预测站点相应的客流等级。

4.3 新线开通后站点客流等级预测

9号线延伸段开通后，线网的拓扑结构发生了一系列的变化，同时各个站点的图论指标也会发生相应变化，利用上文的程序能够轻松获取新线站点及随之发生变化的既有线站点的图论重要度。根据站点图论重要度等级对新线开通初期的站点客流等级进行预测，由此求出预测所得的部分既有站点客流等级见表6。

表6 既有站点部分车站客流等级预测表

为了验证预测结果的优劣，绘制出既有站点的预测等级与实际客流等级间的差值分布，如图4所示。

图4 站点两类分类下的差值分布

由图4可以看出，预测的等级误差在2以内的车站数目达264个，占总数的86.8%，可见该预测方法能够有效地反映站点的实际客流情况，具有很强的可用性。

5 结束语

从图论的方法出发选择Space-L方法对上海轨道交通线网进行拓扑结构建模，选取衡量站点重要度的3个指标，并从自身、空间土地利用和流量的三个角度评价车站的重要性，同时引入站点至4个城市中心的最短路径指标，全面地对车站指标进行评估。基于K-means聚类算法，利用Python编程求得的图论中线网站点指标以及各站至中心站点的最优路径为类别参数，对全网站点进行聚类研究。根据聚类结果，上海轨道交通站点可分为10类，利用实际进站客流数据、分类好的各个站点的客流等级数据分别与图论重要度等级进行相关性分析，得出其分别与图论重要度等级呈强正相关关系，说明随着图论等级的上升，客流等级也会有所提升，因此能够根据新线开通前后站点重要度的变化来反映实际客流等级的变化，为新线开通站点的客流等级预测提供了新的角度和方法。