地铁乘客乘降时间分析与优化

王 通， 郝妍熙， 胡 华， 刘志钢

(上海工程技术大学 城市轨道交通学院， 上海 201620)

0 引 言

城市轨道交通具有运量大、快速、安全、准时等优点，在城市公共交通体系中发挥着不可替代的作用。目前，上海地铁路网客流均处于上升的趋势，运能运量矛盾逐渐显露并且将在一段时间内持续存在。如何提升列车旅行速度，满足未来增加开行列车对数需求，成为了提升线路整体运能和服务水平的重要因素之一。

乘客乘降时间是城市轨道交通列车停站时间的重要组成部分。因此，在城市轨道交通停站时间编制与修订研究中，对乘客乘降行为和时间展开研究，并基于AFC数据和乘客乘降行为特征分析来建立停站时间估计模型，对提高城市轨道交通系统的旅行速度与运行效率具有重要意义[1]。

1 乘客乘降时间估计方法研究

1.1 乘客乘降时间估计模型

乘客乘降时间是城市轨道交通列车停站时间的重要组成部分，对乘客上下车行为与时间特点的把控，将直接影响列车停站时间的确定，从而对城市轨道交通运营组织管理产生影响。对此拟做阐释论述如下。

1.1.1 乘客乘降时间影响因素分析

乘客乘降时间可表示为站台上候车乘客数与乘客平均乘降车时间的乘积，一辆列车停站过程中必要的乘客乘降时间取决于各车门前乘客乘降时间的最大值。因此，列车停站时间中的合理乘降时间值与列车各车门平均乘降人数、各车门乘降人数分布不均衡系数和乘客平均上下车时间等参数有关[2]。列车各车门平均乘降人数受进出站人数、列车发车间隔和车门数的影响；各车门乘降人数分布不均衡系数受站台楼扶梯数量及分布、乘降人数规模、站台客流组织等因素的影响；从前文分析可知，乘客平均乘降时间又受到乘客行为特征、乘客素质(上下车秩序)、是否携带行李、车内拥挤程度和列车剩余座位数等因素的影响。因此，考虑多个影响因素建立停站时间估计模型将是一个复杂庞大的工程，亟待后续的深入系统研究。

根据对上海地铁运营数据的可获得性和模型的实用性，本文选取列车上车人数、列车下车人数、车门数量、列车发车间隔和列车车厢拥挤度(用断面满载率表示)为主要影响因素，在对其进行参数分析与标定的基础上建立乘客乘降时间估计模型。

1.1.2 模型基本假设

由于列车实际停站时间取决于最大客流车门处的乘客上下车时间，因而计算时不仅要考虑不同车站的客流分布规律，还要考虑乘客在站内的移动情况，以便于数据的统计分析。此外，对于给定的客流，研究希望得到最小的列车停站时间。很明显，最小停站时间只有当客流均匀分布在所有车门和车厢时才能取得。故针对以上考虑，给出如下假设：

(1)乘客在列车各车门都进行上、下车活动，并且各车门处上、下车人数不均匀分布；

(2)上、下车乘客比较集中，在地铁列车开启车门前已经做好了上、下车的准备；

(3)乘客严格按照先下后上的秩序进行，上、下车客流不互相干扰；

(4)对于岛式站台，忽略对向客流间的相互干扰；

(5)停站时间与各车门处上车、下车人数是相互独立的线性关系；

(6)假设乘客无滞留情况，候车乘客在列车到达后即能全部上车[3]。

1.1.3 乘客乘降时间估计模型

列车在车站停站过程中所需最小的乘客乘降时间，即在正常追踪时间间隔下，保证站台候车乘客以正常的速度上下车即按下车门或屏蔽门关门按钮所需的时间，即安全停站时间。

列车在车站停站过程中应保证拥挤度最高的关键候车区各车门乘客的乘降时间需求，即停站时间应小于等于列车各车门的需求乘降时间的最大值。对应公式可表示为：

(1)

因此，得到车站j某运行方向(上行或下行)上的乘客乘降时间估计模型，即：

(2)

其中，Tj表示车站j的某运行方向的乘客乘降时间估计值，(单位：s)；Pj表示车站j某单位时间内(小时或15 min或更短的时间间隔内，本项目为15 min)单向进站客流量，人/15 min；Qj表示车站j某单位时间内(15 min)单向出站客流量，人/15 min；m表示车站j的某单位时间内(15 min)的单向列车预定发车列数，列/15min；n表示车站j的某运行方向停站列车的总车门数，门/列；δ表示各车门乘降人数的不均衡分布系数；t均表示乘客人均乘降时间，s/人。

上述估计模型中，Pj、Qj可以基于上海地铁票务清分系统推估获取，m、n可以根据上海地铁列车运行图和各线路列车车型及编组数等数据计算获取。因此，考虑多个影响因素对各车门乘降人数分布不均衡系数和乘客平均乘降时间进行估计，是本文的重点和难点。

本文基于上海地铁现状各站车门乘降人数分布不均衡系数和乘客平均乘降时间的大量视频调查数据，分析其主要影响因素，在此基础上建立各车门乘降人数分布不均衡系数和乘客平均乘降时间的参数分层估计方法；进一步，用标定的地铁列车乘客乘降时间估计模型对上海地铁各站乘客乘降时间进行估计，并通过与实际值的对比分析，对模型估计效果进行评价和验证。

1.2 车门平均乘降人数估计

1.2.1 参数估计

列车各车门的平均乘降人数估计，计算公式如下：

(3)

其中，qj表示超高峰15 min车站j每列车每车门的平均乘降人数；Pj表示超高峰15 min车站j的单向进站客流量；Qj表示超高峰15 min车站j的单向出站客流量；m表示各线路超高峰15 min列车发车对数；n表示各线路的列车车门数。

1.2.2 参数校验

为了验证估计人数的准确性，下面进行乘降人数估计值与实际值的相关性分析，数据采用上海地铁某日各站上下行进出站AFC数据。

相关分析是分析客观事物之间相关性的数量分析方法。许多事物或现象之间总是相互联系的，并且可以通过一定的数量关系反映出来。

相关分析具有能够判断变量之间有无联系、把握相关关系的方向与密切程度等作用。利用相关性分析可以判断乘降人数估计值与实际值是否有关联及其密切程度。本报告利用皮尔逊(Pearson)系数进行两者的关联性分析。Pearson相关系数计算公式如下：

(4)

线性相关的方向通过相关系数的符号来表示，“+”号表示正相关，“﹣”表示负相关。相关系数的数值范围是介于-1与 +1之间：如果|r|越接近0，表明2个变量越没有线性相关关系；如果|r|越接近1 ，则表示2个变量越完全线性相关。乘降人数估计值与实际值的散点图及相关系数计算值见图1、图2。显著性水平为0<0.05，说明乘降人数估计值与实际值显著相关。相关程度系数r=0.608，说明两者显著相关。可见，基于AFC分方向进出站数据的车门平均乘降人数估计值可以反映各站乘客的实际乘降人数分布特征。

图1 乘降人数与车站列车实际人数散点图

Fig. 1 Scattered point diagram of boarding and landing passenger number and actual number of station trains

图2 推估人数与实际人数的相关性分析

Fig. 2 Analysis of the correlation between the estimated number and the actual number

1.3 乘降人数车门分布不均衡系数估计

1.3.1 参数定义

站台候车客流是动态变化的，在不同时段、不同方向、不同车门的乘降人数分布具有很大的不均衡性，而这种不均衡性是影响列车停站时间的重要因素。如前所述，列车的停站时间取决于某一扇车门最大的乘降人数与其所耗费的乘降时间。因此，本项目定义乘降人数车门分布不均衡系数如下：

(5)

其中,δ表示乘降人数车门不均衡系数；tmax表示1列车最大的乘降时间；t列均表示1列车各车门的平均乘降时间。

1.3.2 参数推估思路

本次研究通过视频数据采集和计算各站各车门的乘降人数、乘降时间和车门分布不均衡系数；利用相关性分析方法分析车门分布不均衡系数和车站下游断面满载率、列车各车门平均乘降人数的相关性，从而找到车门分布不均衡系数的主要影响因素；在此基础上，基于概率统计的方法，以主要影响因素为依据，对乘降人数车门不均衡系数进行分层估计。

1.3.3 乘降人数车门分布不均衡系数的估计方法

本文基于概率统计的方法，以车门平均乘降人数为依据，对乘降人数车门分布不均衡系数进行分层估计。首先，绘制车门分布不均衡系数累计频率分布图，见图3。

图3 乘降人数不均衡系数累计频率分布图

Fig. 3 Accumulated frequency distribution map of unbalanced coefficient of passengers and landers

根据车门分布不均衡系数的累计频率分布图，以10%为累计频率分段，分别计算该频段下的车门平均乘降人数，见表1。

表1 车门不均衡系数的累计频率分段值

Tab. 1 Accumulated frequency segmentation value of door unbalance coefficient

累计频率/%列车不均衡系数车门平均乘降人数0-101.00-1.157.314 81510-201.15-1.307.370 37020-301.30-1.356.903 84630-401.35-1.425.944 44440-501.42-1.507.125 00050-601.50-1.553.981 48160-701.55-1.614.638 88970-801.61-1.63-80-901.63-1.723.194 16790-1001.72-1.804.103 333

从表1可见，车门平均乘降人数随每百分之十的车门不均衡系数的递增而递减：在0-30%的范围内，即不均衡系数值在1-1.35，乘降人数在7人以上；在30%-50%的范围内，即不均衡系数值在1.35-1.5，乘降人数在6-7人内；在50%-70%的范围内，即不均衡系数值在1.5-1.6，乘降人数在4-6人内；在70%-100%的范围内，即不均衡系数值在1.6-1.8，乘降人数在4人以下。因此，按照车门平均乘降人数对车门分布不均衡系数进行分层，见表2。

表2 列车不均衡系数的分层与估计

由表2可见，基于车门平均乘降人数分层区间：[0, 4], (4, 6], (6, 7], (7, ∞)，可以将乘降人数车门分布不均衡系数划分为4层：1-1.35，1.35-1.5，1.5-1.6，1.6-1.8。分别计算这4层区间的车门分布不均衡系数的均值，分别为1.22，1.42，1.53，1.69。基于车门平均乘降人数的车门分布不均衡系数可写作如下数学形式：

(6)

其中，δ表示乘降人数车门分布不均衡系数，q表示车门平均乘降人数估计值。

1.4 人均乘降时间估计

(1)参数定义。乘客人均乘降时间是影响停站时间的重要因素，根据国家标准《地铁设计规范GB50157》，乘客人均乘降时间建议值为0.6 s/人。实践中，地铁乘客上下车速度受到很多因素的影响,如车门宽度、乘客年龄、气候条件等，导致其实际人均乘降时间存在一定波动和差异，因此在进行乘降时间估计时不能仅简单引用0.6 s/人的标准建议值。本文基于上海地铁10号线的视频数据，调查统计超高峰15 min时段部分车站各三列车所有车门的乘降时间与乘降人数数据，通过式(7)计算得到一组人均乘降时间值，即：

(7)

其中，t人均表示车门人均乘降时间；t门表示某车门的乘客乘降时间；q门表示某车门的乘客乘降人数。

(2)参数推估思路。通过人均乘降时间实际值的累计频率分布确定其合理取值范围，在此基础上分析人均乘降时间的影响因素，并基于影响因素对人均乘降时间进行聚类估计。

1.4.1 根据累计图，确定人均乘降时间的限值

本文通过视频数据调查与采集了约1 000个乘客人均乘降时间数据值，其累计频率分布图如图4所示。

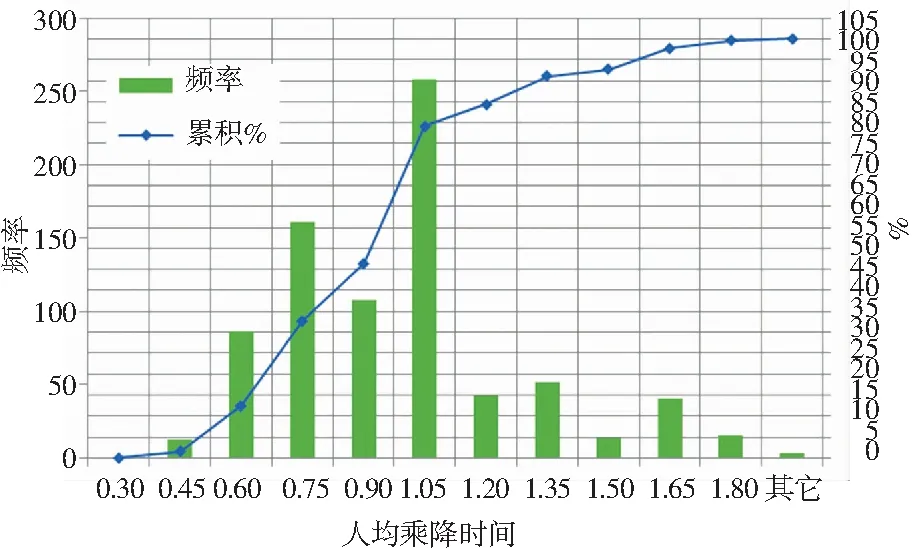
图4 人均乘降时间累计频率分布图

Fig. 4 Accumulated frequency distribution map of average boarding and landing time

由图4可见，85%的人均乘降时间分布在0.5-1.35的范围区间。为消除两端极大极小值对人均乘降时间的影响，本文取0.5-1.35作为人均乘降时间的合理范围值。

1.4.2 人均乘降时间估计函数

人均乘降时间的分段估计函数如下：

(8)

其中，δ表示乘降人数车门不均衡系数；ε表示车站下游断面满载率；q表示车门平均乘降人数估计值。

2 上海地铁10号线各站乘客乘降时间优化方案分析

2.1 上海地铁10号线乘客乘降时间优化方案

本文对上海地铁10号线各站乘降时间进行估计，具体步骤如下：

(1)利用各时段超高峰15 minAFC进站客流量Pj以及出站客流量Qj、列车在该15 min内的开行对数m、列车车门数n(列车编组数*每编组的车门数)，通过式(1)计算得到各站上下行方向的每车门平均乘降人数估计值；

(2)基于每车门平均乘降人数估计值qj，根据式(5)确定列车车门分布不均衡系数估计值δ；

(4)根据每车门平均乘降人数估计值qj和车站下游断面满载率ε，根据式(8)确定人均乘降时间估计值t均;

(5)根据式(8)，计算各站乘客乘降时间估计值，即：

(9)

根据上述估计方法，计算得到10号线各时段各站的上、下行乘降时间。早高峰时段上行方向的乘降时间估计值最大，为325.4 s；平峰时段上行方向的乘降时间估计值最小，为136.9 s。上下行总乘降时间估计值在早高峰最大，为597.2 s；在双休日时段最小，为288.9 s；而在平峰和晚高峰时段分别为292.8 s和550.3 s。虹桥2号航站楼、虹桥路、交通大学、陕西南路、新天地、老西门、南京东路、天潼路、海伦路、四平路是换乘站，由于存在换乘客流，因此其乘降时间比其他一般车站乘降时间的估计值大；其中老西门与南京东路的换乘客流最大，因此其乘降时间也最大。

2.2 对比分析

各时段总乘降时间估计值与图定值对比分析结果见表3。从表3分析可知，由于估计值受乘降时间上限值影响，乘降时间估计值能并没有较好地反映实际客流规律，而乘降时间图定值多数是经验估计值，缺乏对各站司机作业时间和乘客乘降时间的细分要素估计，因此乘降时间估计值与图定值之间存在差值，且总估计值均小于总图定值。10号线各站乘降时间的估计值与图定值差值在双休日时段最大，其总差值为-659 s；在早高峰时段最小，其总差值为-193 s；平峰和晚高峰时段的总差值分别为-447 s和-230 s。

表3 各时段总乘降时间估计值与图定值对比分析

Tab. 3 Comparison and analysis of total boarding and landing time estimates and graph fixed values in different periods

乘降时间上行下行总和估计值与图定值总差值早高峰总图定值400390790总估计值325272597-193平峰总图定值370370740总估计值137156293-447晚高峰总图定值390390780总估计值282268550-230双休日总图定值474474948总估计值145144289-659

从各站的停站时间估计值与图定值的偏差看，在早高峰时段，上行方向各站的偏差较小，而下行方向的各站偏差较大，其中，海伦路站下行方向和四平路上行方向的偏差最大，其乘降时间估计值与图定值的差值分别为14 s和-14 s；在平峰时段，上行的偏差较大，而下行方向的各站偏差较小，其中，南京东路站上行方向的偏差最大，其乘降时间估计值比图定值小23 s；在晚高峰时段，上行方向各站的偏差较小，而下行方向的各站偏差较大，其中，豫园站下行方向偏差最大，其乘降时间估计值比图定值小15 s；在双休日时段，上、下行方向的偏差均较大，其中，南京东路站上行方向的偏差最大，其乘降时间估计值比图定值小27 s。4个时段乘降时间估计值均有显著减少的车站为南京东路站。

3 结束语

本文基于AFC数据和乘客乘降行为特征分析建立乘客乘降时间估计方法，对乘客乘降时间影响因素进行实地调查分析，同时也对上海地铁10号线乘客乘降时间实地调查分析，并提出了乘客乘降时间优化建议。数据分析表明乘客乘降时间的合理分配是提高列车运行效率的重要途径。本文研究成果可为地铁运营管理人员制定与优化合理停站时间提供依据。