基于K-means的矩阵分解推荐算法

张荣梅, 陈 彬, 张 琦

(河北经贸大学 信息技术学院, 石家庄 050061)

0 引 言

当下，随着大数据时代的来临，信息资源过度膨胀，形成了“信息爆炸”的现象。为了缓解这种情况带来的信息过载、数据冗余、选择困难等问题，越来越多的专家学者已然开始关注起推荐系统领域的研究。推荐系统是通过分析用户的历史数据，以及项目等其它辅助信息，推测出用户潜在的偏好需求，进而为用户提供个性化的项目推荐。常见的传统推荐技术是基于内容的算法、基于协同过滤的算法及混合算法[1]。其中，协同过滤算法应用较为广泛，Goldberg等人[2]于1992年提出了协同过滤的概念，最初应用在Tapestry System上用于过滤电子邮件。这是通过引入其它用户的兴趣来对当前用户进行推荐，只是涉及用户的历史交易记录，而不依赖用户和项目的属性特征。但协同过滤算法存在数据稀疏[3]和冷启动问题[4]。于洪等人[5]为了更好地解决物品冷启动问题，提出了一种附加用户时间权重的算法，对用户评论时间与项目发布时间加以计算研究，但由于很多标准数据集中缺少时间戳的属性，其作用范围有限。针对于此，为了改进协同过滤算法，本文将K-means聚类算法与矩阵分解技术相结合，提出一种基于K-means的矩阵分解推荐算法(Matrix Decomposition Based on K-means，KMMD)，引入了用户属性信息，在提高推荐精度的同时，有效改善用户冷启动问题。

1 基于K-means的矩阵分解推荐算法(KMMD)

1.1 Funk-SVD矩阵分解算法

基于内容的推荐和基于用户画像的推荐[6]都是聚焦于待推荐用户自身的属性信息或交易记录，并没有考虑过其它用户的数据是否会对当前用户产生推荐影响，在召回率和精确度上不能进一步提高。而矩阵分解[7]作为协同过滤的一种重要方法，不仅将待推荐用户自身的属性考虑在内，还吸收借鉴了其它用户的数据信息，来实施推荐。且矩阵分解算法将庞大的用户-项目评级矩阵分解为多个矩阵存储，大大减缓了磁盘存储压力。

矩阵分解采用Funk-SVD，是通过将用户-项目评级矩阵Rm×n进行分解，得到可以表示用户和项目特征的2个低维的抽象隐因子矩阵：Um×k表示m个用户的k维隐因子矩阵，Vn×kT表示n个项目的k维隐因子矩阵，使得Um×k·Vn×kT≈Rm×n。使用重构后的评级矩阵来预测用户对未知项目的评分。对于矩阵中的缺失项，在参数更新时选择忽略不计，不对其进行操作，而只针对有效数据进行参数训练。

(1)

其中，损失函数由误差平方和正则化项组成，引入正则化项可以防止训练结果的过拟合。

而训练过程是使用梯度下降降低损失函数，其数学公式可表示为：

(2)

(3)

其中，α是学习率参数，表示每次更新的快慢。

传统的矩阵分解算法多采用传统的SVD矩阵分解方式[8]。传统SVD分解后会得到3个矩阵：U、∑和V。其中，∑是一个对角矩阵，表示U和V矩阵在每个维度上的重构重要度可通过该对角矩阵进行降维，但存在对矩阵求逆等操作，致使计算复杂度高。而本文实验采用的是Funk-SVD分解方式，借鉴线性回归的思想，通过最小化均方误差来寻求最优的用户和项目的隐含向量表示，其维度可直接调整。Funk-SVD用2个矩阵就可以实现SVD三个矩阵的重构效果，在一定程度上提高了运算效率。

1.2 K-means聚类

由于传统矩阵分解算法只使用用户对项目的评级信息，其推荐精度上限难以进一步提升，所以引入用户属性信息，经K-means聚类分析再进行矩阵分解运算，提高算法推荐能力。K-means是一种将数据按策略划分为某几种类别的聚类算法[9]，其中K表示聚类的类别种数，即质心的数量，means表示均值。K-means聚类之前的预处理过程可分述如下。

(1)提取用户基本属性信息，User=(Age,Gender,Occupation)，构建用户属性矩阵U。

(2)对于非数值的离散型数据，进行one-hot编码[10]数值化处理。one-hot编码是将原某类型属性按照其种类进行编码，编码结果是只有一位为有效值1，其余位都是0。年龄属性已经是数值型属性，所以不做处理。性别是二元属性，分为“男”和“女”，所以分别编码为[0]和[1]。职业属于标称属性，包含多种类别，按照类别总数S构建长度为S的编码串，并由先后出现顺序为其置“1”编码，在MovieLens-100K数据集中共出现有21种职业类型，数据集中最先出现的“technician”职业的one-hot编码为[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1]，紧接着出现的“writer”职业的one-hot编码为[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0]，以此类推。然后所有属性拼接组合成稀疏的用户属性向量，对于“年龄=24，性别=男，职业=技术员”的用户User_a=(24, man, technician)，经如上处理后得到的用户属性向量为User_a′=[24 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1]。

(3)embedding处理。经由one-hot编码后的数据必然是稀疏的，所以将其进行embedding处理，即是将原稀疏向量与固定转换矩阵做内积变换，转化为稠密向量，即：

(4)

得到由用户稠密属性向量构建的用户属性矩阵，就可以进行K-means聚类分析了。算法1的设计步骤见如下。

算法1K-means。用于聚类划分的K-均值算法，其中每个簇的中心(质心)都用簇中所有对象元素的均值来表示[11]

输入：K表示簇的数目；D为包含n个对象元素的数据集

输出：K个簇的集合

(1)从D中任意选取K个对象作为初始簇的中心；

(2)repeat

(3)根据簇中对象元素的均值，将每个对象分配到最相似的簇；

(4)更新簇均值，即重新计算每个簇中对象的均值；

(5)until不再发生变化。

采用K-means聚类算法提前对用户进行聚类分析，可减小构建的用户-项目评级矩阵规模，若不做预处理，则需要对全部用户和全部项目信息构建评级矩阵，这样在矩阵分解时会严重降低算法效率，占用大量内存。而通过聚类构建小规模的近邻用户-项目矩阵，可加快矩阵分解计算，利于算法模型的整体效率，且额外的聚类代价远远小于大规模矩阵分解的消耗代价。

K-means聚类处理为当前用户构建了近邻集合，由于兴趣偏好相似的用户倾向于购买相同项目的思想，所以在近邻用户中进行数据分析，可有效提高推荐的准确度，实验证明这样的设计思路的确对推荐中召回率和精确度有提升效果。

1.3 KMMD算法设计

本文将K-means算法与Funk-SVD矩阵分解算法结合，提出了KMMD算法。算法2的设计流程详见如下。

算法2KMMD, 基于K-means的矩阵分解算法

输入：User表示包含m个用户的用户属性(User)数据集；Ua表示当前待推荐用户的属性信息；Ratings表示包含m个用户对n个项目的部分评级数据集；L表示推荐列表长度；K表示聚类簇数

输出：针对用户Ua的推荐列表List

(1)对User进行K-means聚类分析，划分为K个簇：C1,C2,...,CK；

(2)ifUa== 老用户 then

(3)提取Ua所在簇Ca的所有对象元素，并从Ratings中筛选出这些对象元素的评级数据，构建近邻用户-项目评级矩阵R；

(4)将R进行Funk-SVD分解，得到U和V两个低秩矩阵；

(5)矩阵重构：R’ =U·V；

(6)在重构评级矩阵R’中找到对Ua的重构预测向量ra；

(7)else将Ua与簇中心求相似度，找到Ua归属的簇Ca；

(8)从Ratings中筛选出Ca簇中对象元素的评级数据，构建近邻用户-项目评级矩阵R；

(9)将R进行Funk-SVD分解，得到U和V两个低秩矩阵；

(10)矩阵重构：R’=U·V；

(11) 求得Ua与Ca中各对象元素的相似度Sima,i(i∈Ca)；

(12) 加权计算求得Ua的预测评级：

(5)

(13)end if

(14)对ra中各个项目预测值排序，选出前L个项目组成推荐列表List。

2 实验与结果分析

本实验采用数据集MovieLens-100K，使用召回率和精确度作为模型评价指标，进行参数影响及参数确定的实验，得到效果最佳的KMMD算法模型，并将其与2种传统算法CBbyPortrait和MFbySVD做了对比实验。研究可得解析详述如下。

2.1 数据集

基于MovieLens数据集[12]是由明尼苏达大学的Grouplens研究项目收集整理。数据集获取地址：http://files.grouplens.org/datasets/movielens/。实验具体选用的是MovieLens-100K。MovieLens-100K数据集包含943名用户对1 682部电影的10万条评分记录，评分采用5分制(1，2，3，4，5)。该数据集主要包含3个文件：用户数据文件(u.user)、项目数据文件(u.item)和评分文件(u.data)，其中u.user包含用户的人口统计信息，字段有：用户标识(user id)、年龄(age)、性别(gender)、职业(occupation)和邮编(zip code)；u.item包含电影项目的信息，字段有：电影标识(movie id)、电影标题(movie title)、上映日期(release date)、视频发布日期(video release date)、数据源链接(IMDb URL)和类别属性(genres)；u.data包含完整的评级数据，字段有：用户标识(user id)、项目标识(item id)、评分(rating)和时间戳(timestamp)。

2.2 模型评估指标

本文采用混淆矩阵[13]中的精确度(Precision)和召回率(Recall)进行算法模型评估。涉及到的参数和计算方法如下：TP(True Positive)表示将正类预测为正类；TN(True Negative)表示将负类预测为负类；FP(False Positive)表示将负类预测为正类，也称为误报；FN(False Negative)表示将正类预测为负类，也称为漏报。

其中，召回率(Recall)和精确度(Precision)的计算公式为：

(6)

(7)

2.3 参数选取

为了得到KMMD算法的最佳效果，首先进行控制变量实验，测试重要参变量的取值变化对算法效果的影响。KMMD算法的重要参变量有3个：K-means聚类的聚类种数K；矩阵分解的训练步数Steps；推荐列表长度L。而Funk-SVD的学习率参变量α依据经验设定为0.000 2。实验随机选取MovieLens-100K数据集的80%作为训练集，余下20%作为测试集。研究中，将分3组进行控制变量实验。研究内容详见如下。

(1)Steps固定取50，L固定取10。观察参数K的变化影响，结果如图1所示。

(a) 粗粒度范围

(b) 细粒度范围

图1中，实线实心倒三角表示精确度的变化趋势，虚线实心圆圈表示召回率的变化趋势。图1(a)是在[5,100]范围内粗粒度验证K值变化对实验精度的影响，可以看到，随着K值逐渐增大，召回率和精确度都是先增后降的趋势，其极值在K取25-35的范围内取得。为进一步获取最佳K值的推荐效果，图1(b)给出了在[25,35]闭区间范围内细粒度实验仿真。由实验结果可知，当K值取29时，算法的当前推荐效果最佳。

(2)K固定取29，L固定取10。观察参数Steps的变化影响，结果如图2所示。

图2 Steps值变化影响

由实验结果可知，随着Steps值的增大，召回率和精确度总体趋势都是下降的，当Steps值取[80,110]区间值时，其实验效果较好，为方便实验进行，将Steps值取为100。

(3)Steps固定取100，K固定取29。观察参数L的变化影响，结果如图3所示。

图3 L值变化影响

由实验结果可知，随着L值的增大，召回率会呈现递增趋势，而精确度总体是呈现递减趋势，最终逐渐收敛平稳。为确定L取具体何值时，可使推荐的整体效果较好，研究中还对图3实验结果进行F度量表示，即：

(8)

F度量赋予了召回率和精确度相等的权重，是两者的调和均值。其结果如图4所示。可知在L值取15时，F值最高，综合推荐效果最好。

图4 F度量值变化

2.4 对比实验

为了验证KMMD算法模型的真实效果，选取了2种推荐算法模型与本文提出算法进行比较。这2种算法的设计表述如下。

(1)CB(Content-based Recommendation)：基于内容的推荐模型，通过召回用户日志文件获取与用户有过交互的项目信息，再根据项目的属性特征学习用户的偏好兴趣，可构建用户画像，并以此计算用户与待推荐项目匹配度，推荐与其过去已购买过物品相似度高的商品。

(2)MF(Matrix Factorization)：传统基于矩阵分解的推荐模型，通过用户对项目的显式评分数据构建用户-项目评分矩阵，使用SVD奇异值分解矩阵后再进行重构，预测用户对未购买过的商品的评分，进行推荐。

对比实验在MovieLens-100K数据集下进行，使用了十折交叉验证法。根据控制变量实验结果，对KMMD算法的参数选取了K=29，Steps=100，L=15。实验结果对比见表1。对表1分析后可知，其研究结果的重点陈述见如下。

(1)召回率表现的是推荐效果的灵敏性，从该值的角度来分析，KMMD算法的效果最好，其相较于CB算法提升了15.64%，相较于MF算法提升了154%。说明在灵敏性上，KMMD算法有了很大的提升。

(2)从精确度来看，KMMD算法的效果远高于其它两个算法，比CB提升了30.43%，比MF提升了103%。可见，KMMD算法在推荐的精确度上也有很不错的表现。

由实验可得，KMMD算法在召回率和精确度上都有很大提升，能为用户提供更准确的推荐。

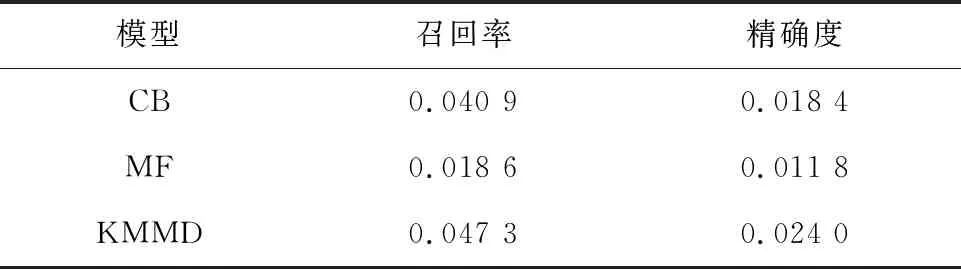
表1 召回率和精确度对比

2.5 模型预测

该部分通过实验验证提出的KMMD算法可以对新用户进行有效推荐。实验是在包含943名用户的MovieLens-100K数据集基础上，仿照其数据格式，构造了2名用户基本属性数据作为新用户，作为用户冷启动实验对象，数据如下：

(1)用户a：年龄=24，性别=男(M)，职业=技术员(technician);

(2)用户b：年龄=50，性别=女(F)，职业=作家(writer)。

实验结果见表2。

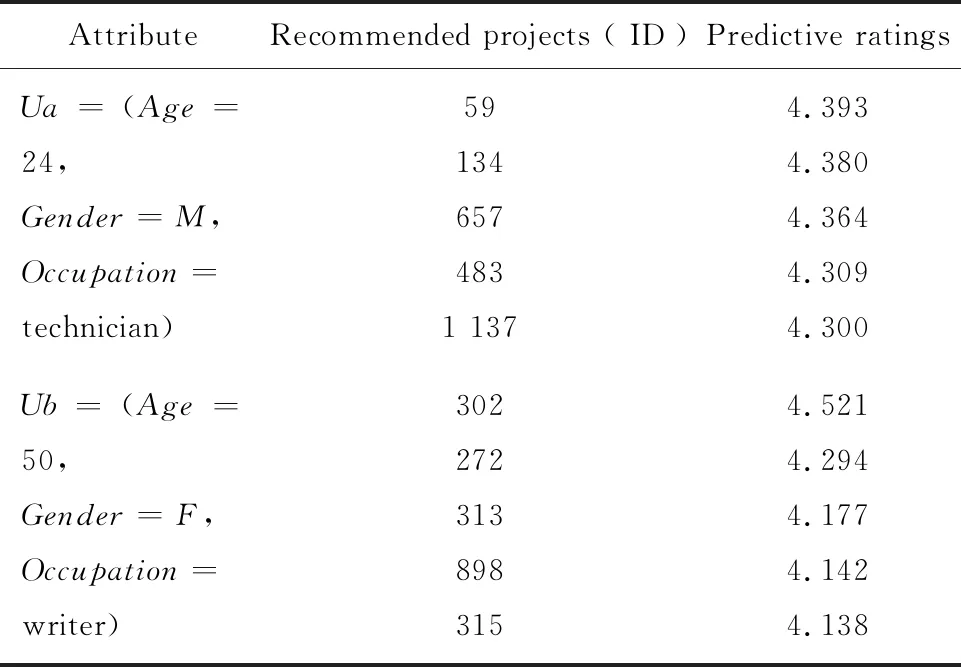
表2 用户冷启动预测

实验结果说明，KMMD算法可以对新用户进行项目推荐，结果以评级高低排序。KMMD算法有效改善了用户冷启动问题。

3 结束语

将聚类算法与协同过滤思想相结合，提出了一种基于K-means的矩阵分解推荐算法。首先通过实验分析不同参数对KMMD算法的召回率和精确度变化影响，得出算法的高效率参数配置。并进行对照实验，比较传统推荐算法与KMMD算法在MovieLens公开数据集上的实验效果，得出结论，融合K-means聚类后的矩阵分解算法确实有助于推荐准确度的提高，且在引入用户属性数据的条件下，有效改善了用户冷启动问题。但该算法对项目冷启动问题还难以处理。后续工作是将深度学习技术与推荐算法相融合，构建多种推荐算法的组合排序，力求进一步提升推荐算法的准确度，并有效解决项目冷启动问题。