设问启发联想 解题更加自然

李 健

（浙江省临海市第五中学）

巴甫洛夫学派认为：学习就是形成暂时联系，暂时联系就是联想，就是获得有关事物关系的知识.当进行新的学习时，利用知识，利用已获得的诸联系，这就是理解.因此，知识的学习和研究是离不开联想的.但在平时的教学中，我们经常遇到学生面对一道问题时束手无策，作为教师应该做好解题的引导作用.但如何更加自然地引导学生的解题过程，而不是让他们去被迫接受教师的观点？笔者认为数学解题的思考过程实质上是已知与未知之间一系列联想、整合的过程，因此通过设置“问题串”启发学生利用联想，能够比较自然地求解问题.

一、例题呈现

题目如图1，在△ABC中，已知∠BAC=90°，AB=AC，D为AC的中点，AE⊥BD于点E，延长AE交BC于点F.求证：∠ADB=∠CDF.

图1

二、“联想法”思维过程

思维过程如图2所示.

图2

1.由条件联想

（1）由 ∠BAC=90°，AB=AC，可以联想得出新的结论①：△ABC是等腰直角三角形.

（2）由点D是AC中点，可以联想得出新的结论②：AD=DC.

（3）由AE⊥BD，可以联想得出新的结论③：∠AED=∠AEB=∠BEF=∠DEF=90°.

……

联想出这些新的结论后，我们可能会发现很难再继续联想下去，并且联想出来的新的结论也是分散、凌乱的，能否帮助我们求证问题呢？我们还需要从结论展开联想.

2.由结论联想

要证明“∠ADB=∠CDF”，我们学过哪些方法？这个问题很容易让我们联想到如下方案.

方案1：全等三角形可以证明角相等；

方案2：通过计算角度可以判断角度相等；

方案3：利用相似三角形可以证明角相等；……

结合“由条件联想”得出的结论，我们可以确定“利用全等三角形”“利用相似三角形”的方案更具有可行性.但是观察图形，我们会发现图中缺少包含∠ADB和∠CDF的全等三角形和相似三角形，因此我们会想到构造这样的三角形，但是如何构造比较合理呢？这给解题又造成了困扰，接下来让我们再结合图形模型展开联想.

3.由模型联想

仔细观察图形，其中存在着一些基本模型，它们可以引导我们快速联想出一些新的结论.

模型1：如图3，是初中几何中常见的一个图形，通过联想得出新的结论.

新的结论④：∠DAE=∠ABE，∠ADE=∠BAE.

新的结论⑤：△ABD∽△EBA∽△EAD.

模型2：如图4，根据等腰直角三角形的特征，作斜边上的高，发现新的结论.

新的结论⑥：△ABG和△AGC都是等腰直角三角形.

新的结论⑦：∠BAG=∠GAC=∠B=∠C=45°.

图3

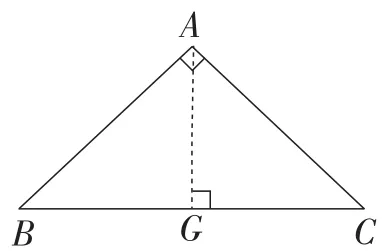
图4

4.以问题为目标，反思整理

面对前面获得的大量信息，我们可能会感到迷茫，如何将这些信息有效组合起来求解问题？这个环节需要我们将这些联想得到的条件、求解方案和模型进行整理、重组，以问题为目标展开反思，避免解题过程中出现偏离问题的现象.我们可以通过自问的形式强化这个环节.

求解这个问题还需要哪些条件（方法）？如何实现？

我们熟悉这个问题吗？联想到的条件与这个问题有怎样的联系？

这个条件（模型）对这个问题起到什么作用？

……

三、解法展示

解法1：由模型2自然地添加辅助线.如图5，作AG平分∠BAC，交BD于点G，

因为∠BAC=90°，

所以∠CAG=∠BAG=45°.

因为∠BAC=90°，AC=AB，

所以∠C=∠ABC=45°.

所以∠C=∠BAG.

由模型1可以写出下面的证明：

因为AE⊥BD，

所以∠ABE+∠BAE=90°.

因为∠CAF+∠BAE=90°，

所以∠CAF=∠ABE.

因为AC=AB，

所以△ACF≌△BAG.

反思：求解问题还需要什么条件？要用什么方法？自然地引导我们进入方案1，明确证明的目标（△AGD≌△CDF）.

所以CF=AG.

因为∠C=∠DAG=45°，CD=AD，

所以△CDF≌△ADG.

所以∠CDF=∠ADB.

证明结束后，教师可以借助图形提出问题：这个图形（如图5）中，还包含了哪些我们熟悉的模型吗？它能为我们提供什么结论？

这个问题促使学生再次观察图形，归纳出模型3：对顶三角形模型（如图6），可以发现结论：∠HAE=∠EBH，△AEG∽△HBG.学生可以将这个模型纳入到模型体系中，为后续的解题提供帮助.

图5

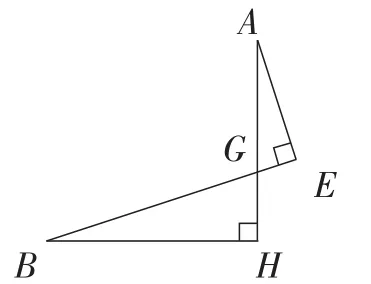
图6

解法2：利用模型1和方案1，可以添加辅助线，延长AF，经过点C作AC的垂线交AF于点I（如图7），这条辅助线可以帮助我们构造出△ABD≌△CAI，从而证明∠ADB=∠AIC.为我们继续证明∠CDF=∠ADB建起一座桥梁，过程如下.

图7

因为AE⊥BD，

所以∠ABE+∠BAE=90°.

因为∠CAF+∠BAE=90°，

所以∠CAF=∠ABE.

因为AB=AC，∠BAD=∠ACI，

所以△ABD≌△CAI.

所以∠ADB=∠AIC.

反思：现在要证明∠CDF=∠ADB，只要证明∠AIC=∠CDF.结合图形，实现△DFC≌△IFC即可.

由△ABD≌△CAI，得AD=CI.

因为点D是AC的中点，

所以AD=DC=CI.

因为AB=AC，∠BAC=90°，

所以∠ACB=45°.

所以∠FCI=∠ACB=45°.

已知FC=FC，

所以△FCD≌△FCI.

所以∠AIC=∠CDF=∠ADB.

解法3：仔细观察模型1、模型2，会发现问题中的∠ADB与∠BAE相等，而∠BAF却被分割成两个角的和（45°+∠HAF），因此我们自然想到把∠FDC也分割成两个角，如果一个角是45°，另一个角与∠FAH相等，由此问题得证.运用方案3构造出相似三角形可以实现目标，如图8，过点A，D分别作BC的垂线，交BC于点H，M.

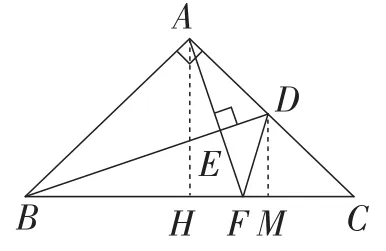
图8

反思：现在要证明∠ADB=∠CDF，只要证明∠BAE=∠CDF=45°+∠HAF（∠FDM）.结合图形，实现△AFH∽△DFM即可.

已知∠AHF=∠DMF=90°，

所以△AFH∽△DFM.

所以∠HAF=∠FDM.

因为∠ADB=∠BAE=∠BAH+∠HAF=45°+∠HAF，∠CDF=∠CDM+∠FDM=45°+∠FDM，

所以∠ADB=∠CDF.

四、总结归纳

教师指导学生对上述三种解法进行相互交流，针对不同联想的角度进行点评和补充.

你是如何自然地想到这种解法？

为什么要添加这条辅助线？你是自然地想到的吗？

遇到这个问题时，我们还会自然想到与它有关的哪些问题？

这个图形中还包含了哪些常见的模型？它可以解决怎样的问题？

如图9，将△AFC逆时针旋转 90°，得到△AF′B.就构造出一个等腰三角形AF′F与一个Rt△F′BF.由此我们又可以自然地联想出许多结论.

……

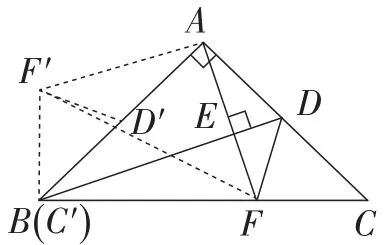
图9

这样的总结不仅使学生掌握几种解决数学问题的方法，更是培养学生联想能力，使他们的知识体系和解题方法得到了扩充.思维更加灵活，联想更加丰富.

五、教学反思

1．“联想法”是基于学生现有认知的自然驱动

联想法解题是基于现有认知经验的基础，对问题和条件的自然生长和构建，然后进行合理整合，分阶段确立目标和实现目标化归，直至问题求解.学生能熟练掌握这种解题方法，要求教师在教学中注重完善学生的知识结构化和系统化.例如，在学习全等（相似）三角形时，教师帮助学生构建全等与相似之间特殊与一般的关系，它们的性质都可以证明对应角相等，那么学生从结论联想，自然会想到构造全等（相似）三角形；学习余角的知识时，教师能够结合图1，让学生探究角度之间的关系，将这个关系纳入到他们的知识系统中，在此题目中，学生就会发现这个模型，并由此联想出一系列结论∠DAE=∠ABE，∠ADE=∠BAE，△ABD∽△ABE∽△ADE，促进学生对问题的思考.知识越系统，经验越丰富，联想就越深入、越广泛，解题也就越自然.

2.抓住问题本质，联想顺应自然

章建跃博士曾说：要逐步养成从基本概念、基本原理及其联系性出发思考和解决问题的习惯，这才是发展思维能力的正道.例如，题目中求证∠ADB=∠CDF，其本质是通过构造“全等三角形”（△CDF≌△ADG或△FCD≌△FCI）或“相似三角形”（△AFH∽△DFM），利用其性质得出对应角相等，因此如何构造全等与相似就成了解题思维的核心，我们要结合题目和模型中提供的角相等、边相等，对应边成比例等条件，再对这些信息进行整合重组，使问题逐步向最基本的概念及性质、原理、方法转化，所以教师在分析问题时要抓住问题的本质和核心，归纳总结出通性、通法，使得解题联想的过程自然流畅.

3．重视“联想法”的训练，使其自然生成

“联想法”是一种解题的思维方式，离不开教师在平时的解题教学中进行渗透，通过设问实现强化，鼓励学生分析、求解问题时展示联想的思维过程.

例如，文中多次通过提问和自问的方式去促使联想的训练.

求解这个问题还需要哪些条件（方法）？如何实现？

我们熟悉这个问题吗？联想到的条件与这个问题有怎样的联系？

这个条件（模型）对这个问题起到什么作用？

遇到问题时，我们还会自然想到与它有关的哪些问题？

通过加强联想训练，使其成为一种思维习惯，从而实现自然生成的目的.

总之，数学解题不能只拘泥于“怎么解”，还应关注解题的方法和策略，不能只拘泥技巧的运用，还应该归纳问题的通性、通法，不能拘泥单纯知识的讲授，还应关注数学知识的整体结构.唯有如此，我们才能提升学生的数学素养，将培养他们的解题能力落到实处.