挖掘美学素材，发展学生的美学素养

李国凯

（安徽省合肥市庐阳区教研室）

我国著名数学家华罗庚教授说过：“就数学本身而言，是壮丽多彩、千姿百态、引人入胜的……，数学美应是数学中能带给人愉悦的东西.”数学之美充满了整个世界，如图形的对称、布局的合理、形式的整齐、表达的简洁，无不体现出数学中的美.

对学生进行数学美的教育，培养学生欣赏美的能力，有助于学生树立学习信心，激发学习兴趣，挖掘学习潜能，促进学生思维的发展，使学生形成积极的情感态度和价值观，培养学生的创造能力.

因此，在教学中，教师要善于挖掘和运用教材中隐含的数学美，充分展示其独特的本质特征，使学生在获取知识的同时，激发学生浓厚的学习兴趣，进而唤起学生的审美体验，体会数学教学的美学价值.

一、在公式、规律的推导中，感知数学语言的简洁美

在为美国发射的去茫茫太空中寻觅地球外文明的“先驱者号飞船”（探测器）征集所携带的礼物时，华罗庚教授曾建议带上数学中用以表示勾股定理（毕达哥拉斯定理）的简单、明快的数形图（如图1），它似乎应被宇宙所有文明生物所理解.

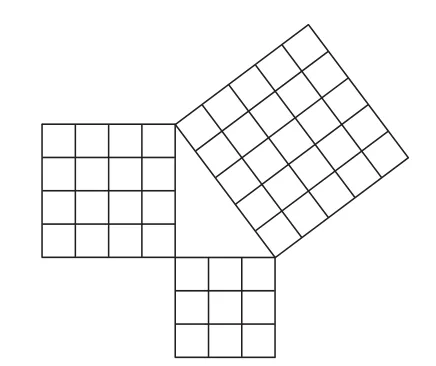
图1

数学语言就是这么神奇，不需要烦琐的文字表述，却有“此时无声胜有声”的作用.教学中，体现数学语言简洁美的素材有很多，如公式的表达.教师要善于抓住这些美学素材，让学生感知到数学语言的神奇与魅力.

例1（1）观察如图2所示的图形与等式的关系，并填空.

图2

（2）观察图3，根据（1）中结论，计算图中黑球的个数，用含有n的代数式填空.

1+3+5+…+(2n-1)+( )+(2n-1)+…+5+3+1=____．

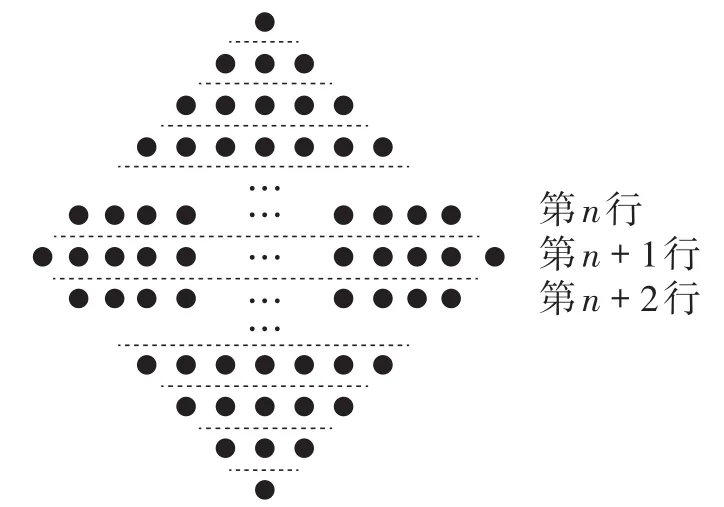
图3

教学过程设计如下.

环节1：观察.

第（1）小题中，图2左侧部分是由相同的圆点拼成的三角形和正方形，对比发现，虽形状不同，但圆点的个数相同，进而可以用等式来表示圆点个数，也就是图2右侧部分等式所表达的含义.

环节2：类比.

根据观察图2发现的规律，引导学生类比写出1+3+5+7=42；

环节3：推广.

根据图2所给规律，可知第n个图中左右两侧圆点的个数变化，得出等式1+3+5+7+…+(2n-1)=n2.

教学进行到这里，只是得出了所要求的结论，教师还需及时引导学生用文字语言描述一下图中圆点个数的变化规律，进而体会用文字语言表述的内容，也可以用这一简单的等式来表示，体会数学语言的简洁之美.

环节4：证明.

若要证明1+3+5+7+…+(2n-1)=n2，可以引导学生采用倒位相加法来证明这个结论，为解决第（2）小题做铺垫.

环节5：解决问题.

解决第（2）小题的方法较多，现提出两种仅供参考.

方法1：可将图3中的黑球分三部分，第1行到第n行，第n+1行，第n+2行到第2n+1行，再结合第（1）小题的规律即可得出结论．

方法2：引导学生发现图3是由两个正方形点数叠加而成（如图4），从而可以直接得出1+3+5+…+(2n-1)+(2n+1)+(2n-1)+…+5+3+1=(n+1)2+n2.

图4

【评析】这是一道数形结合的找规律题，用数去表达图形中的规律，体现了图形语言和符号语言的简洁之美.另外，方法2的观察角度之巧，思维方法之妙，无不体现图形叠合之美，以及数学符号的简洁美.虽然方法简洁、简单，但是内涵丰富，这正是数学的迷人所在.

二、在运动变化中，探究几何图形的动态美

动态几何问题一般是以几何图形为载体，以函数为背景，以运动变化为主线，蕴涵多种解题思想的一种题型，主要包括动点、动线、动形等方面的问题.这类问题往往集几何、数与式、方程与函数于一身，数形结合、动中有静、静中有动，能较好地锻炼学生的空间想象能力与演绎推理能力，具有极强的综合性.

在初中几何教学中，有很多可以进行拓展与推广的重要结论.在教学中，教师要引导学生去发现动点或者动线在运动变化过程中某些不变的规律或结论，让学生体验动态图形的奥秘与美感，进一步培养学生数学学习的乐趣.

例2如图5，在矩形ABCD中，点P是矩形内一点，连接PA，PB，PC，PD，则有结论：PA2+PC2=PB2+PD2.

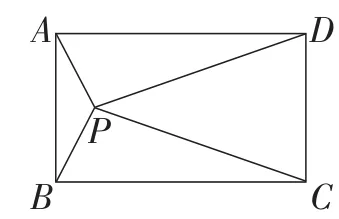
图5

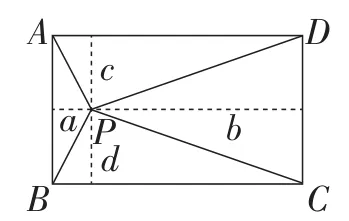
图6

解析：如图6，过点P分别作AB和BC的平行线，然后利用勾股定理得出PA2+PC2=a2+b2+c2+d2，PB2+PD2=a2+b2+c2+d2，所以PA2+PC2=PB2+PD2.

此时只是解决了问题，没有挖掘出题目中的美学素材.教师要引导学生发现结论的一般性，于是就有了以下的三个变式.

变式1：如图7，移动点P，使点P移动到矩形ABCD的某一边上，那么结论PA2+PC2=PB2+PD2还成立吗？

图7

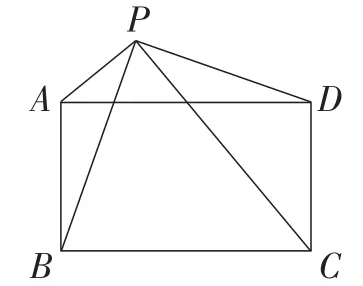
图8

变式2：如图8，拖动点P，使点P移动到矩形ABCD之外，那么结论PA2+PC2=PB2+PD2还成立吗？

变式3：如图9，拖动点P，使点P移动到矩形ABCD所在平面之外，那么结论PA2+PC2=PB2+PD2还成立吗？

图9

显然，可以证明结论都是正确的.

【评析】把点P从矩形内部移动到矩形边上，再移动到矩形所在的平面上，进而把点P拉起到立体空间，由二维到三维，体现图形变化但规律不变的研究思路，是初、高中内容衔接方面一个很好的案例.

三、在问题提出与解决过程中，探究数学规律的奇异美

学生学习中，经常会遇到一些疑难问题.此时，教师要引导学生积极思考，通过合情推理去发现问题，进而提出问题、分析问题，并解决问题.学生在研究数与形的内在规律时要学会合理运用转化思想，学会思考特殊与一般之间的逻辑关系，学会欣赏数学变化规律的奇异性，进而形成美的体验.

例3如图10，在△ABC中，AD是边BC的中线，O是AD上的中点，过点B，C分别作BM∥AC，CN∥AB，过点O作一条直线分别交边AB，AC于点F，E，交BM，CN于点H，G.求证：FH+EG=2EF.

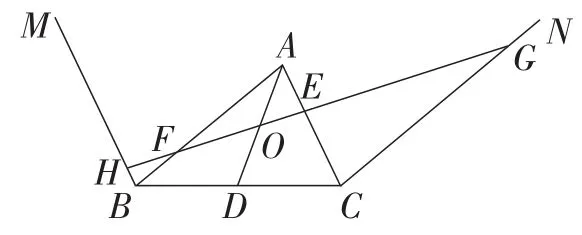
图10

环节1：化繁为简，体现数学等式的结构美和数学问题的转化美.

将等式FH+EG=2EF两边同时除以EF，可以得因为BM∥AC，CN∥AB，所以.只需要证明即可.

于是，将例3转化为如下问题.

变式：如图11，在△ABC中，AD是△ABC的边BC的中线，O是AD的中点.求证：

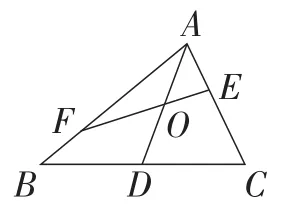
图11

环节2：在特殊情况下寻找解决问题的突破口，体现解题策略之美.

上述变式解决起来同样复杂，可以从特殊情况入手，寻找解决问题的方法.

情况1：如图12，当EF∥BC，且E，F分别为AC，AB的中点时，结论显然是成立的.

图12

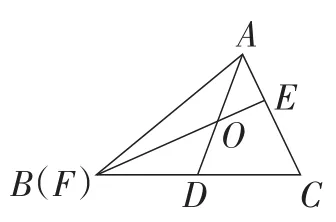
图13

情况2：如图13，当点F与点B重合时，，我们只需要证明即可.

解决问题的方法有很多，现提供两种添加辅助线的方法.如图14，过点D作DG∥BE，交AC于点G；如图15，过点A作AG∥BC，交BE的延长线于点G.证明过程略.

图14

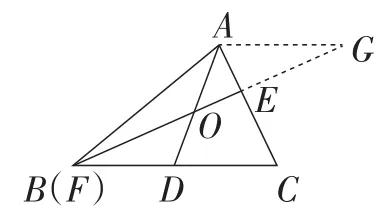
图15

环节3：类比.

变式的解题思路与例3有异曲同工之处.例3的解题思路如下.

如图16，过点A作AG∥BC，交FE的延长线于点G，交CB的延长线于点H，易证得AG=DH.

图16

此题的证明方法还有很多，在此不再赘述.

环节4：拓展延伸，在线段的运动中研究图形的内在规律美.

上述所有问题的出发点都基于点F在AB上，点E在AC上.若过点O的直线与三角形一边的延长线相交，结论会怎样呢？

拓展：如图17，在△ABC中，AD是边BC的中线，O是AD上的中点，假设过点O的直线交边AB于点F，交AC的延长线于点E，结论还成立吗？

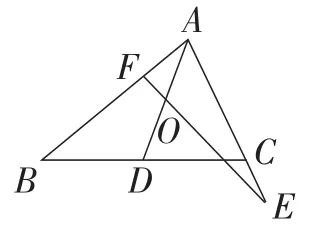
图17

图18

解：不成立.理由如下.

如图18，过点A作AG∥BC，交EF的延长线于点G.易证得AG=DH.

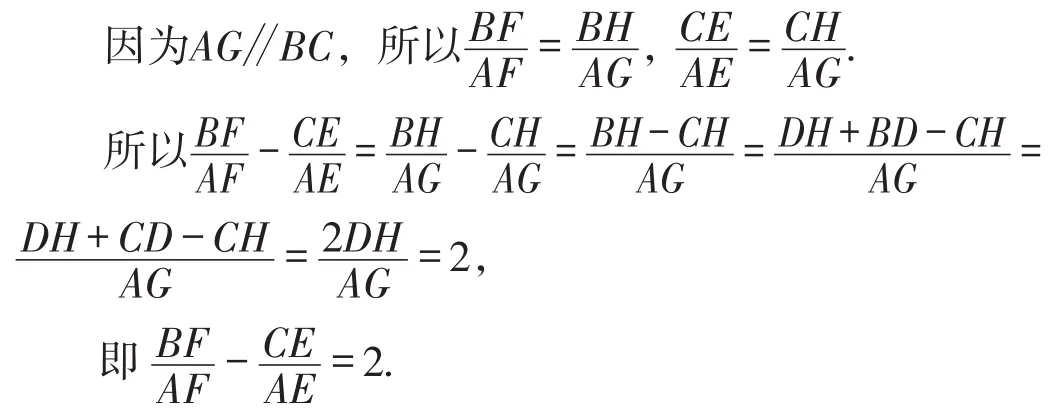
【评析】将一道复杂的问题，通过改变结论转化成一个新问题，体现了数学表达式的形式结构之美.在解决新问题的过程中，利用特殊位置把陌生的问题转化成熟悉的问题，既验证了结论的正确性，又为下一步一般情形的证明提供了可借鉴的思路与方法.由特殊到一般地研究图形变化中的内在规律，尤其是在拓展延伸环节，把线段EF绕线段AD的中点O旋转，进一步探究数学结论的变化规律，既体现了几何图形的灵动之美，又体现了数学规律的奇异之美.

四、在操作变换中，感知图形的对称美

在初中平面几何中，有很多非常美丽的图形，如等腰三角形、正方形、正多边形、圆等，图形美在对称，包括轴对称、旋转对称等.对称美在建筑、艺术等日常生活中有着广泛的应用.在教学中，教师要积极挖掘这些图形的美学素材，通过让学生感知、操作等教学环节，培养学生的美学意识，进而形成美学素养.

例4如图19，已知在△ABC中，∠BAC=36°，AB=AC，点P为△ABC所在平面内一点，且点P与△ABC的任意两个顶点构成的△PAB，△PAC，△PBC均是等腰三角形，求满足上述条件的所有点P的个数.

环节1：发现美.

通过师生画图操作和讨论交流，画出如图20所示的对称图形.

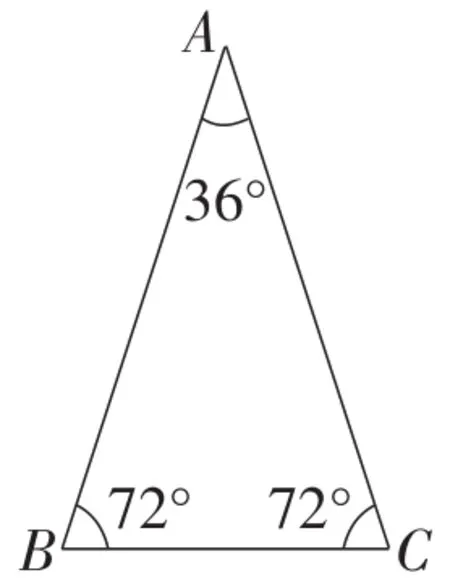
图19

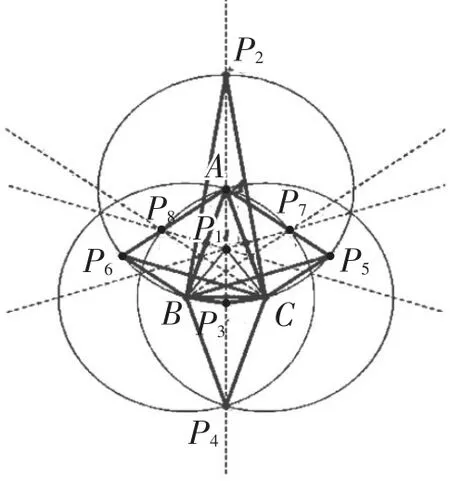
图20

环节2：感悟美.

通过学习新知，了解黄金三角形的对称美，黄金分割比例的和谐美.

在等腰三角形中，有一个非常特别的三角形，它的顶角为36°，每个底角为72°.如图19，通过构造相似，计算出等腰三角形的底与腰成黄金比，即，因此把这种特殊的等腰三角形叫做黄金三角形.

环节3：欣赏美.

教师引导学生联系生活，欣赏生活中的黄金三角形.例如，文明古国埃及的金字塔形似方锥，大小各异，但这些金字塔底面的边长与高之比都接近于0.618.又如，著名画家达·芬奇的作品《蒙娜丽莎》构图完美地体现了黄金分割在油画艺术上的应用.经过画面分析，蒙娜丽莎的头和两肩在整幅画面中三点构建了一个近乎完美的黄金三角形，使得这幅画看起来是那么的和谐和完美.

又如，大家最熟悉的正五角星图案（如图21），它的每一个角都是一个黄金三角形.正五角星是由正五边形对角线连接组成，正五边形的任意两条对角线的交点都是这两条对角线的黄金分割点.

图21

【评析】黄金三角形的底角平分线分对边为黄金比，并分成两个较小的等腰三角形．教学中，教师可以让学生在操作画图的基础上，通过旋转、对称等变换，使学生在操作中发现对称美，在学习新知中感悟黄金分割比例的和谐美，并在实际生活中欣赏图形的对称美、和谐美，以及数与形的融合之美.

五、结束语

我国现代著名数学家徐利治教授指出：所谓数学美的含义是丰富的，如数学概念的简单性、统一性，结构系统的协调性、对称性，数学命题与数学模型的概括性、典型性，还有数学规律的奇异性等，都是数学美的具体内容.当我们悟出了一个数学公式，发现了一条数学规律，解决了一道数学难题，我们的心中也就会有一种特别愉悦的兴奋感，就像欣赏一首优美的乐曲一样充满了愉悦之情.这是数学美育的最高境界.