钢弹簧浮置板隔振道路的模态分析

邹锦华，陈 伟，黄龙田，陈海斌，李碧坤，蔡仕晨

（1. 广东工业大学 土木与交通工程学院，广东 广州 510006；2. 广东省建筑设计研究院，广东 广州 510010）

随着社会经济的发展，振动对环境的影响已经引起越来越多的重视。建设中的广州市万博商务中心核心区地下空间，被称为广州市结构最复杂的地下空间，将在四层的地下空间里，集交通、停车、商业、市政于一体，总建筑面积接近180万 m2，地下道路 2.26 km。为了减小市政道路车辆运行引起的振动

对地下商场安全和舒适性及地下结构的影响，在道路设计中，采用钢弹簧浮置板新型道路结构作为交通车辆引起振动的主要隔振措施。即在部分地下空间顶板上方再做一层可浮置的混凝土道路板，用钢弹簧隔振器予以支撑，构成浮置板结构道路，隔离市政交通荷载引起的结构低频振动，以达到减振降噪的目的[1]。

浮置板隔振道路是一种新型的结构，在国内属于首次示范应用，无相关经验可供参考。然而在轨道交通方面，浮置板轨道应用及研究成果已有很多。梅早临等[2]研究了浮置板轨道系统的固有频率对减振的影响规律。向俊等[3]建立了列车−浮置板轨道结构竖向振动分析模型，对浮置板的动力学性能进行了研究。邹锦华等[4]建立了地铁−浮置板轨道过渡段耦合振动模型，研究了浮置板过渡段动力特性和设计参数。韦凯等[5]分析了不同固有频率钢弹簧浮置板轨道在不同合建结构形式中的适用性。李增光等[6]将浮置板简化为自由边界的Kirchhoff薄板，研究了浮置板的高阶模态。刘维宁等[7]研究了弹簧刚度和支承间距等设计参数对低频振动特性和隔振性能的影响。王颖轶等[8]利用车轨耦合动力学研究了短型浮置板的传递特性和板下结构参数对于系统振动响应的影响。程珊等[9]通过建立车辆−浮置板轨道−桥梁耦合模型研究了钢弹簧刚度和浮置板密度对高架钢弹簧浮置板轨道减振特性的影响规律。Lombaert等[10]采用模态分析法研究了浮置板轨道的设计参数。Hui等[11]采用三维有限元模型研究了浮置板与高架结构箱梁的耦合振动及避免高阶共振的措施。由于轨道交通采用的钢弹簧浮置板尺寸较小，大小相对固定，而市政道路浮置板由于路面较宽及不宜设置过多接缝原因，长度和宽度都很大，浮置板道路本身的动力性能和隔振性能也需要进一步的研究。

本文通过建立万博商务中心地下空间结构上方钢弹簧浮置板道路的三维有限元模型，对浮置板、地下空间和浮置板应用于地下空间上方时的整体结构进行模态分析，对比分析3种结构的低阶固有频率和振型，并进一步研究了传导比，以检验和评价钢弹簧浮置板的减振效果，为钢弹簧浮置板隔振道路的实际工程应用提供参考。

1 浮置板道路设计概况

1.1 浮置板道路隔振原理

砼浮置板道路结构是把沥青混凝土铺装在钢筋混凝土浮置板上形成连续路面，浮置板置于可调的钢弹簧隔振器上，相邻浮置板及浮置板与普通道路之间用密排粗钢筋剪切连接，浮置板两侧用橡胶弹性材料固定，形成连续体系的质量−弹簧隔振系统。基本原理就是在道路和基础间插入一固有频率远低于激振频率的线性谐振器，以减小传入结构和基础的振动，降低下部结构振动和噪声。隔振系统的效果主要取决于浮置板的质量、弹簧的刚度及相互作用，其主要动力参数应根据上部车辆荷载的动态条件确定。与轨道交通采用的钢弹簧浮置板不一样的是，市政道路浮置板长度和宽度都很大，因而具有很多高阶的振动模态，但对隔振效果起关键作用的仍然是低阶的固有振动模态。由已知的振动理论，荷载传递系数VF为[12]

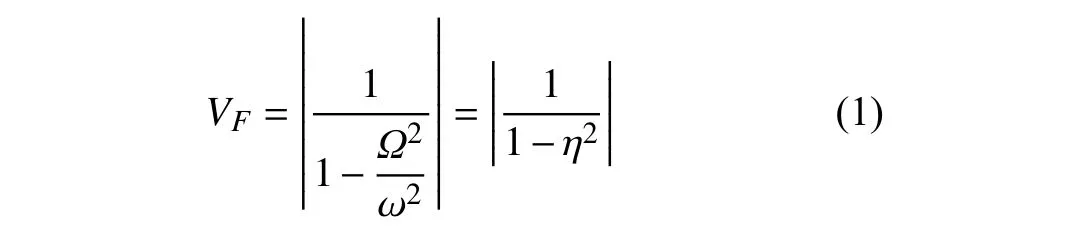
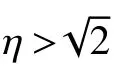
1.2 砼浮置板道路设计概况

钢弹簧砼浮置板示范道路位于万博中央商务区核心区万惠一路，设计时速40 km/h。浮置板全长90 m，宽10.0 m，厚0.45 m。钢弹簧置于钢套内部，上部与浮置板钢筋相连，下部直接放置在地下空间顶部，布置间距为1.8 m×1.8 m，弹簧刚度为5.3 kN/mm，浮置板之间以及与普通道路连接处设置剪力铰。浮置板质量密度为2.6×103kg/m3，弹性模量为3.25×104MPa，泊松比为0.2，结构阻尼比为0.05。地下空间为半敞开二层地下结构，地下一层为商场，地下二层为内部通道和城市综合管廊。地下一层层高5 m，顶板厚0.8 m，由左侧的两排立柱和右侧的剪力墙支撑。地下二层平均层高5 m，顶板厚1.2 m，均由剪力墙支撑。浮置板和地下空间结构砼强度等级均为C40，如图1所示。

2 浮置板道路模态分析

2.1 有限元模型及网格划分

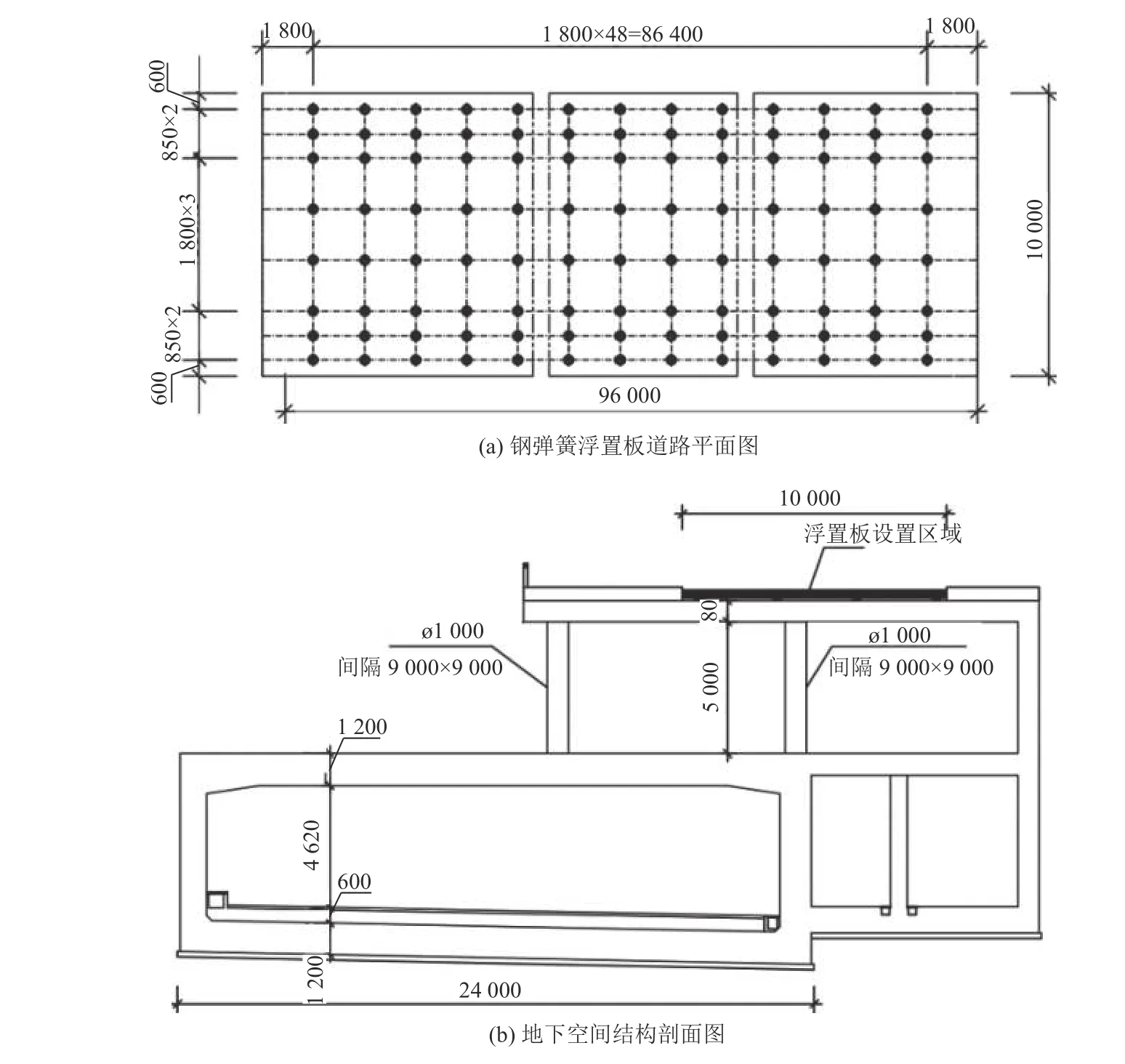
图1 钢弹簧浮置板道路示意图(单位：mm)Fig.1 Schematic plot of steel spring floating slab road

根据实际工程设计资料，应用有限元软件Ansys，建立地下空间及其上方浮置板隔振道路三维有限元模型。浮置板和钢弹簧分别采用板单元和弹簧单元模拟。楼板和剪力墙采用板单元模拟，立柱采用梁单元模拟，其余均采用实体单元模拟。地下结构基底为固定约束，侧边界为弹性约束，弹簧刚度根据土层特性选取。钢弹簧隔振器构造决定了浮置板只能产生竖向变形，因此将模型中的弹簧单元除竖向以外的其他自由度约束。考虑到市政道路两侧及相邻浮置板对四周位移的约束，对浮置板模型两端沿板长方向的自由度和两侧沿板宽方向的自由度也进行约束；钢弹簧用弹性连接单元模拟，下端用一般支承将6个方向的自由度全部约束。有限元模型如图2所示。

2.2 计算结果及分析

2.2.1 固有频率

钢弹簧砼浮置板具有高阶振动模态，但对隔振效果起关键作用的是低阶竖向固有振动模态，分别提取钢弹簧浮置板、地下空间以及整体结构(地下空间+浮置板)的前6阶竖向固有频率，如表1所示。

图2 万博项目地下空间及其上方浮置板道路三维计算模型Fig.2 Three-dimensional computing model of underground space and floating slab road above Wanbo project

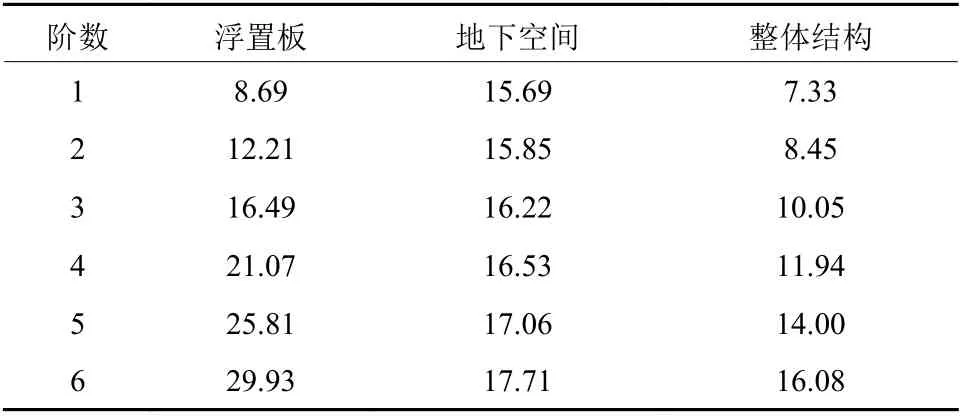
表1 结构前六阶竖向固有频率Table 1 The first six natural frequencies of the structure Hz

为了提高隔振效果，应尽可能降低钢弹簧浮置板的一阶固有频率。由表1可以看出，浮置板基频为8.69 Hz，在地下空间结构增加钢弹簧浮置板后，基频由15.69 Hz降至7.33 Hz。根据国内外已有的测试资料，可知公路汽车荷载产生的激振能量频段主要集中为10～40 Hz[1]，要有效的隔振，要求道路隔振的基频应尽量小于7 Hz，以避开交通荷载振动频率范围，这说明设计钢弹簧砼浮置板的减振效果非常明显。另外，3种结构模型的各阶固有频率的间隔均较小，浮置板的各阶固有频率相差在4 Hz左右；地下空间和整体结构的各阶固有频率均相差在1.0 Hz左右。

2.2.2 振型

振型是结构体系的一种固有特性，与固有频率相对应，每一阶固有频率对应一种振型。图3为整体结构的前六阶振型图。图3可以看出，前五阶振型均较为相似，主要体现为钢弹簧浮置板的振动，且随着阶数增大，浮置板的振动更加剧烈；第六阶时主要表现为地下空间顶板的振动。这说明交通荷载频率基本不会触发地下空间除地下一层顶板外的其余构件振动。

3 传导比分析

在钢弹簧浮置板道路模型施加单位简谐荷载，计算得到的钢弹簧最大支座反力。最大支座反力与单位简谐荷载的幅值之比为传导比[13]，公式为

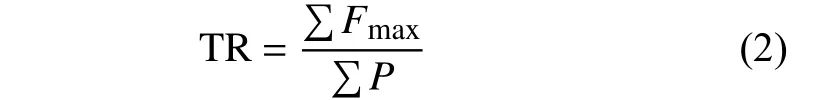
其中，Fmax为传递到钢弹簧支座的最大反力，P为简谐荷载的幅值。图4为3种结构的传导比分析图。

当传导比小于1时，表示系统对外界激励起隔振作用。由图4可知，对于地下空间结构，传导比峰值为3.53，对应峰值频率15.75 Hz，与地下空间结构的第一阶频率15.69 Hz接近；传导比曲线大于1，说明在交通荷载激振(10～40 Hz)时，荷载从路面传至地下空间后产生了放大效应，将会对结构产生不利影响，需要进行有效的隔振减振。对于钢弹簧浮置板结构，传导比的峰值为8.58，对应的峰值频率为8.75 Hz，与钢弹簧浮置板结构的第一阶频率相等；当激励荷载频率大于10 Hz时，传导比的值已小于1，这说明钢弹簧浮置板有着良好的减振隔振性能。对于浮置板与地下空间组成的整体结构，与钢弹簧浮置板的传导比规律较为接近；传导比的峰值为9.89，出现在频率值为7.25 Hz附近，与整体结构的第一阶频率7.33 Hz相接近；当频率处在该路段交通荷载激振(10～40 Hz)范围内时，整体结构的传导比值最大为0.878，钢弹簧浮置板起到了良好的隔振减振效果，有效地减少了交通荷载对地下空间结构产生的振动影响。

4 结论

本文应用ANSYS有限元软件对新型的钢弹簧浮置板道路进行模态分析，分析了钢弹簧浮置板隔振道路对地下空间结构的固有频率、振型以及传导比的影响。

(1) 钢弹簧浮置板道路、地下空间、整体结构一阶频率分别为8.69，15.69和7.33 Hz；钢弹簧浮置板应用于地下空间上方时可起到有效的减振作用。

(2) 从振型上看，低频时主要表现为钢弹簧浮置板的振动，中高频时主要表现为地下空间顶板的振动。

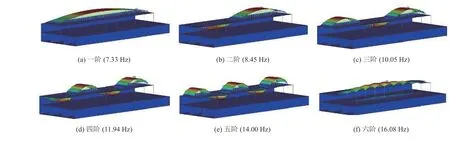
图3 整体结构的前六阶振型Fig.3 The first six order mode shapes of integral structure

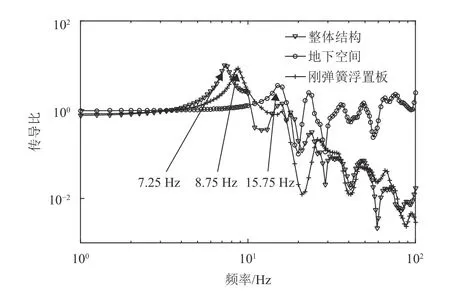
图4 3种结构的传导比Fig.4 Conductivity ratio of three structures

(3) 3种结构的传导比峰值均出现在基频附近，增加钢弹簧浮置板后地下空间结构传导比小于1，可起到有效的减隔振作用。

通过本文分析可知，新型钢弹簧浮置板隔振道路对减振隔振效果很明显，可以为实际工程应用提供参考价值和分析依据。