紫铜粗糙表面的光谱双向反射分布函数测量研究
杨博文,马王杰慧,刘彦磊,刘玉芳
(河南师范大学物理与材料科学学院,河南 新乡 453007)
1 引 言
双向反射分布函数(Bidirectional Reflectance Distribution Function,BRDF)是表征目标表面空间光学反射特性的物理量,能够有效描述目标表面的光学反射特性[1-2]。BRDF在目标光散射计算、杂光分析、计算机图像处理、地物遥感、目标识别和材料的光学性能研究等领域有着广泛应用[3-7]。因此,近几十年来关于BRDF的研究工作从未间断过,这些工作主要集中在BRDF测量装置的研制[6,8-12]、材料BRDF的测量、BRDF模型的建立和BRDF的应用等方面[13-15]。准确描述目标表面的视觉特性是BRDF的重要应用之一。众所周知,目标的颜色与光在介质中的吸收和散射特性有关,光泽则与光的反射方向和强度有关[16],光谱BRDF能够很好地描述目标的视觉特性,对工艺品视觉效果方面的设计具有重要意义。
紫铜是一种常见的金属材料,由于其具有良好的导电性能被广泛应用于电气工业。紫铜具有暗红的金属光泽,不仅能够呈现出现代感,还能体现出沉稳、高贵的品质,是铜饰中应用最广泛的材料。测量紫铜表面的光谱BRDF能够提供紫铜的光学反射特性,为紫铜工艺品加工设计提供准确的视觉特性,有助于降低加工成本和优化设计效果。
关于铜表面BRDF的测量研究很少见到报道,戴景民等[17]测量了25~500 ℃的温度范围内铜表面的BRDF,分析了温度对测量结果的影响。结果表明:温度对铜表面BRDF的测量结果有明显的影响。然而,他们测量中采用632.8 nm的He-Ne激光器作为光源,主要研究单波长下温度对测量结果的影响,不能够体现铜表面的光谱反射特性。
本文的主要工作是基于自行研制的BRDF测量装置测量了可见光波段紫铜表面的面内光谱BRDF,并对影响测量结果的因素做了分析。论文的结构如下:第二部分主要介绍本文所采用的BRDF测量方法与测量装置,第三部分介绍样品加工、测试和实验过程;第四部分给出测量结果与讨论;第五部分给出基于Gauss和Lorentz分布的拟合结果与分析;最后对全文工作进行了总结。
2 测量原理与装置
2.1 BRDF测量原理
BRDF的定义最早由Nicodemus给出[1],其将双向反射分布函数fr定义为光辐射的反射辐亮度dLr与入射辐照度dEi的比值,即:
fr(θi,φi,θr,φr,λ)=

(1)
式中,θ和φ分别表示天顶角和方位角,下标i和r分别表示入射和反射,λ为波长。BRDF的物理含义是:来自入射方向的表面辐照度的微增量与其所引起的反射方向上反射辐射亮度增量之间的比值。BRDF定义的几何关系如图1所示。

图1 双向反射分布函数几何关系图 Fig.1 Geometric relationship diagram of incident and reflected beams for BRDF
BRDF的测量方法有绝对测量和相对测量两种。相对测量方法可以减小系统误差,对杂散光也能起到较好的抑制作用。与绝对测量相比,相对测量对设备精度的要求较低,能够节约测量成本。但是,相对测量方法的缺点也比较明显,即必须依赖标准参考试样。首先,目前尚未见到在所有波长和所有环境中均适用的标准参考试样。其次,并不是所有研究单位都具备精密测量标准参考试样的条件,而计量部门提供的往往只是典型的入射和接收几何条件下的数据,与实际测量中的几何条件不一定一致。因此,本文采用绝对测量方法测量紫铜表面的BRDF。
本文采用的BRDF绝对测量方法在文献[18]中有详细介绍,这里仅给出测量表达式:
fr(θi,φi,θr,φr,λ)=
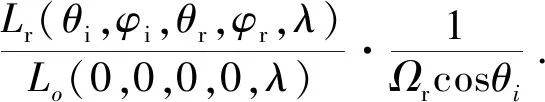
(2)
对于均匀性、稳定性和准直性较好的光源,Lo(0,0,0,0,λ)是与波长有关的函数,完全由光源决定,可以在安放样品前对光源进行测量得到。对于固定的测量装置,探测立体角Ωr是常数,可以根据探测器的探测孔径和探测距离计算得到;角度因子cosθi由入射天顶角得到。根据测量原理知,只需测量反射辐亮度Lr(θi,φi,θr,φr,λ)即可得到待测目标的BRDF。
2.2 测量装置
本文的测量所用装置为一套自主设计的典型传统BRDF测量装置,其通过样品、探测器和光源的配合转动实现不同入射和反射角度下BRDF的测量。测量装置采用氙灯(GLORIA-X500A)作为光源,能够提供入射光的波长范围为300~2 500 nm;采用光栅光谱仪作为探测系统,可探测波长范围为250~2 500nm,光谱分辨率为0.4 nm。转角装置主要包括两个转台和两个转臂,通过它们之间的配合转动可实现不同角度下BRDF的测量。测量装置的设计图如图2所示,转台和转臂的转动范围见表1。

表1 转臂和转台的转动范围
本文实验系统的入射光路和测量光路如图3(彩图见期刊电子版)所示,分别用蓝色和红色箭头表示。光路中M0~ M6是同一型号的保护银膜平面反射镜。虚线框中所示是本文所设计的探测聚焦附件,主要包括3个高透过会聚透镜和一个通光孔径为2 mm的光阑,这样设计的主要目的是为了减小探测系统在样品表面的有效探测面积。理论上讲,安装附件后,探测器只能够探测到来自于透镜L2焦点位置的反射光,能够有效消除反射天顶角对有效探测面积的影响,这是绝对测量方法得以实现的基础。
3 样品制备与测量
本文准备了4个半径为25 mm、厚度为2 mm的圆片状紫铜样品。采用金相磨抛机对样品进行加工以得到不同的表面粗糙度。分别采用400目、600目、800目和1000目的碳化硅砂纸对样品进行打磨,依次标记为1#、2#、3#和4#样品。分别采用丙酮和无水乙醇对砂纸打磨后的样品进行清洗,之后,将样品放入超声波清洗机进行进一步的清洗,以确保样品表面无污垢残留。使用粗糙度仪TR220(时代公司)对处理完成后的样品表面的粗糙度进行测量,测量结果如表2所示。其中Ra、Rq和Rz分别为算术平均粗糙度、均方根粗糙度、轮廓最大高度。
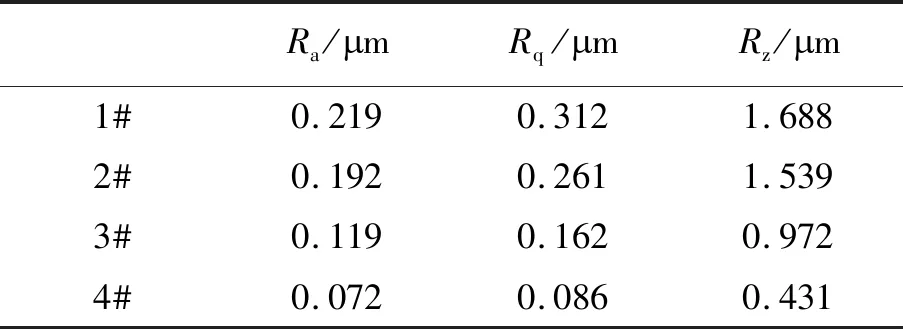
表2 4个样品表面的粗糙度
本文所采用的测量装置是典型的传统BRDF测量装置,需要依靠转角装置实现不同角度下BRDF的测量。这导致测量过程十分耗时,很难实现所有角度下目标表面光谱BRDF的测量。本文的测量中,入射天顶角分别设置为30°、45°和60°,入射和反射方位角分别设定为0°和180°,反射天顶角的范围为-80°~80°,测量间隔在镜面反射方向附近设定为1°,远离镜面反射方向的区域设定为2°;波长范围设置为380~780 nm,间隔为5 nm。如前文所述,本文采用绝对测量方法实现BRDF的测量,测量过程主要包括光源光谱亮度的测量和样品表面反射亮度的测量。首先,取下样品台,将入射天顶角、反射天顶角、入射方位角、反射方位角分别设置为90°、90°、0°、180°,测量氙灯的光谱亮度。然后,安装样品台并放置样品,按照设定的目标依次测量4个样品表面的面内光谱BRDF。在分析测量结果之前需要指出的是:对于粗糙的表面而言,BRDF在一般情况下不可能等于零,然而在本文的测量中出现了等于零的情况,这主要归因于探测器的灵敏度有限。在本文的结果分析中,不再显示BRDF等于零的部分。
4 测量结果与讨论
为了研究紫铜表面的BRDF随波长和粗糙度的变化情况,本文测量了入射天顶角为30°时的面内光谱BRDF,1#~4#样品的测量结果在图4(彩图见期刊电子版)中给出。从图4能够看出,在入射波长的情况下,BRDF随着反射天顶角的增加,先增大后减小,在镜面反射方向达到最大值,这一变化趋势几乎不受波长变化的影响。另外,从图中能够看出,紫铜在380~550 nm波段存在较强的吸收,波长大于550 nm时,随着波长的增加吸收迅速减弱,并且这一变化趋势不受反射天顶角,即观察方向的影响,这与紫铜表面所呈现出的颜色是一致的。在可见光波段,目标的光谱吸收和反射特性很大程度上取决于目标表面颜色,紫铜的颜色是色素色不随观察方向的改变而发生变化。测量结果与紫铜所呈现出的视觉特性是一致的。对比图4中的4幅子图能够发现,不同粗糙度下紫铜表面的BRDF随波长和反射天顶角的变化趋势比较相似。在给定波长的情况下,镜面反射方向的BRDF随着粗糙度的减小而逐渐增大,这是因为随着表面粗糙度的减小,样品表面越来越接近于光学光滑表面,导致镜面反射方向的反射增强。根据图4的测量结果能够得到如下规律:紫铜表面的BRDF随反射天顶角的变化不受波长的影响,随波长的变化趋势不受反射天顶角的影响。如果这个规律正确,那么可以将紫铜的空间光谱反射特性分为光谱反射特性和空间反射特性,即在单波长下研究紫铜表面的空间反射特性,在单个反射方向下研究其光谱反射特性。这样可以大幅度减小BRDF的测量时间和测量成本。
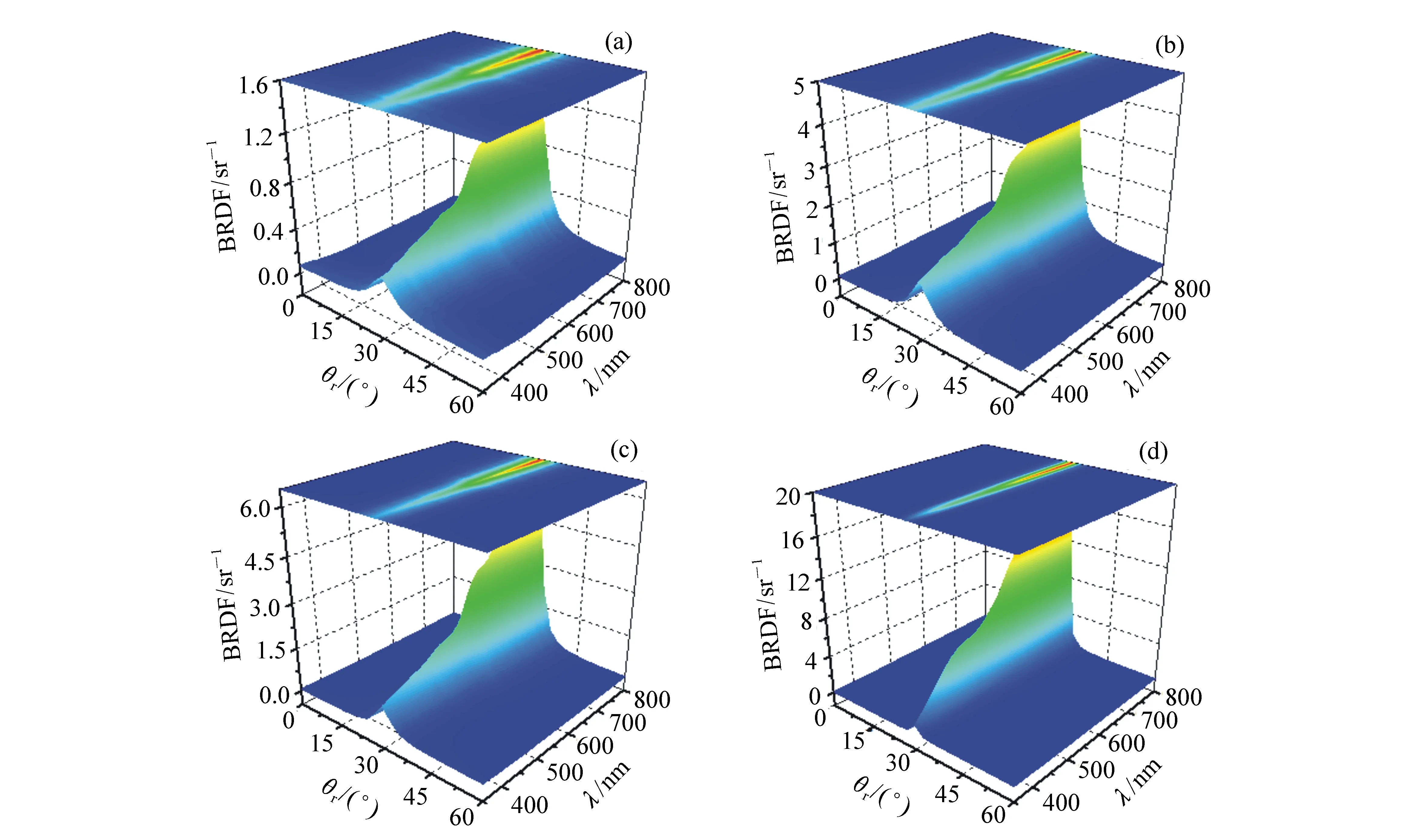
图4 θi =30°时,样品的面内光谱BRDF,(a)~(d)依次为1#~4#样品的测量结果 Fig.4 In-plane spectral BRDFs of samples at θi=30°:(a)1# sample, (b)2# sample, (c)3# sample and (d)4# sample
为了验证上文所述规律的正确性,文中测量了入射天顶角为45°和60°时紫铜表面的光谱BRDF,测量结果分别在图5(彩图见期刊电子版)和图6(彩图见期刊电子版)中给出。从图中可以看出,BRDF随反射天顶角的变化趋势不受波长影响,随波长的变化趋势不受反射天顶角的影响。这很好地验证了上述结规律的正确性,也说明将紫铜表面的空间光谱反射特性分为单入射波长下的空间反射特性和单反射方向下的光谱反射特性是可行的。

图5 θi =45°时,样品的面内光谱BRDF,(a)~(d)依次为1#~4#样品的测量结果 Fig.5 In-plane spectral BRDFs of samples at θi =45°: (a) 1# sample, (b) 2# sample , (c) 3# sample and (d) 4# sample

图6 θi=60°时,样品的面内光谱BRDF,(a)~(d)依次为1#~4#样品的测量结果 Fig.6 In-plane spectral BRDFs of samples at θi=60°:(a)1# sample, (b)2# sample , (c)3# sample and (d)4# sample

图7 650 nm下,BRDF随反射天顶角的变化曲线,(a)~(d)依次为1#~4#样品的测量结果 Fig.7 Curves of BRDF varying with reflectance zenith at 650 nm:(a) 1# sample, (b) 2# sample , (c) 3# sample and (d) 4# sample
为了更清晰地展示紫铜表面BRDF随反射天顶角的变化,本文提取了650 nm下,入射天顶角为30°、45°和60°时4个样品的测量结果,分别在图7(a)、7(b)、7(c)和7(d)中给出。从图7(a)中能够看出, BRDF随着反射天顶角的增加呈现出先增大后减小的趋势,在镜面反射反向附近达到最大值。θi=45°和θi=60°时BRDF随反射天顶角的变化趋势与θi=30°时的相同,这说明入射天顶角对BRDF随反射天顶角的变化趋势没有明显的影响。另外,从图7(a)中能够看出,随着反射天顶角的增加,BRDF在镜面反射方向附近的值逐渐增加。从图7(b)、7(c)和7(d)中能够看出,2#~4#样品的BRDF随反射天顶角的变化趋势与1#样品相同,这说明表面粗糙度对BRDF随反射天顶角的变化趋势没有明显的影响。
为了更清楚地展示粗糙度对测量结果的影响,图8给出了θi=45°时,4个样品在λ=650 nm时的测量结果。

图8 650 nm下,θi=45°时BRDF随反射天顶角的变化曲线 Fig.8 Curves of BRDF varying with refletance zenith at 650 nm, θi=45°
很明显,样品的表面粗糙度对BRDF随反射天顶角变化的趋势没有明显的影响,4个样品的BRDF随反射天顶角的变化曲线均呈“钟形”,曲线的最大值在镜面反射方向。从图8能够看出,粗糙度对BRDF的大小有很大的影响,尤其在镜面反射方向附近。以镜面反射方向为例,随着Ra由0.219 μm减小为0.072 μm,BRDF值由1.81 sr-1增大为16.80 sr-1。另外,随着粗糙度的减小,BRDF随θr变化的曲线变得越来越“高”、越来越“瘦”。这说明,随着粗糙度的减小,样品表面在镜面反射方向附近的反射逐渐增强,偏离镜面反射方向的强度逐渐减小。
从图7的测量结果能够看出,4个样品的BRDF尤其是在镜面反射方向的值随入射天顶角的增大而增大。产生这种影响的原因可以归结为两个方面:(1)随着θi的增大,样品在镜面反射方向的反射增强;(2)角度因子的影响,测量原理式中有cosθi项,随着θi的增大,角度因子逐渐减小,从而导致BRDF增大,在θi较大时更加明显。测量原理中的探测立体角Ωr由探测器的入光孔径和探测器到样品之间的距离决定,测量装置设计完成后,探测立体角为常数。分析测量原理能够发现,fr· cosθi能够很好地描述目标表面的反射强度。为了进一步分析反射强度和角度因子对BRDF的影响,本文给出了不同入射天顶角下镜面反射方向的BRDF与fr· cosθi随角度的变化曲线,如图9所示。测量波长为650 nm,θi的设置范围为20°≤θi≤70°,测量间隔为5°。
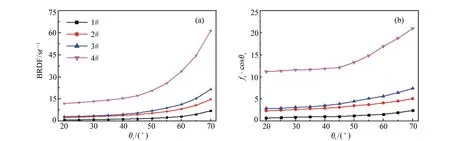
图9 650 nm时,样品在镜面反射方向的BRDF(a)和fr·cosθi(b) Fig.9 BRDF(a) and fr·cosθi(b) at specular direction for the samples at 650 nm
由图9(a)可以看出,在给定天顶角的情况下,BRDF随着粗糙度的增加而减小。对于每一个样品,当θi≤45°时,BRDF随着θi的增大而缓慢增加;当θi>45°时,BRDF随着θi的增大而快速增加。为了消除角度因子cosθi对测量结果的影响,图9(b)给出了不同入射天顶角下镜面反射方向的fr·cosθi。从图中可以看出,fr·cosθi随θi的变化趋势与BRDF的变化趋势相同。图9的测量结果说明,随着入射天顶角的增大,镜面反射方向的反射强度与角度因子对BRDF均有积极作用。
5 实验数据拟合
这部分的主要工作是对测量结果进行拟合,以比较不同分布函数对测量值的拟合结果。现阶段常用的BRDF模型,如Phong模型、Cook-Torrance模型和Ward模型等均采用Gauss分布函数作为基础函数。这是因为大多数BRDF模型将空间反射特性近似看做理想朗伯体与镜面反射的叠加,而Gauss分布比较适用于这种近似。然而,目标表面在远离镜面反射的方向一般都不满足理想朗伯体近似,即使是在BRDF相对测量方法中作为参照的的白板也不是理想朗伯体。寻找更合适的基础函数对BRDF经验或者半经验模型的建立有重要意义。文中选取多种不同的分布函数对测量结果进行拟合,发现采用Lorentz分布得到的拟合结果与测量值最接近,文中给出了入射天顶角为45°时,采用Lorentz分布的拟合结果与采用Gauss分布的拟合结果进行了对比,如图10所示。

图10 θi=45°,λ=650 nm 4个样品的测量与拟合结果 Fig.10 Measuring and fitting results of the four samples at θi =45° for λ=650 nm
从图10能够看出,采用Lorentz分布的拟合结果比采用Gauss分布得到的结果更好。对比这两种拟合结果能够看出,在镜面反射方向附近,Lorentz和Gauss分布的拟合结果与测量值符合的较好。在远离镜面反射方向的角度,采用Lorentz分布的拟合结果优于Gauss分布的拟合结果。这说明采用Lorentz分布作为基础函数建立BRDF经验或者半经验模型,可能得到更好的结果。
6 结 论
本文通过自主设计的BRDF测量装置测量了紫铜表面的BRDF,详细分析了入射波长,入射天顶角,表面粗糙度对测量结果的影响。结果表明:(1)BRDF随波长的变化趋势不受入射和反射角度的影响;(2)镜面反射方向附近的BRDF值随着入射天顶角的增大而逐渐增大,同时受角度因子和样品表面反射强度的影响;(3)测量结果容易受样品表面粗糙度的影响,随着表面粗糙度的增加,BRDF随反射天顶角的变化曲线呈现出越来越“矮”,越来越“胖”的趋势。另外,本文采用不同的分布函数对测量结果进行了拟合,并将得到的最优拟合结果与采用Guass分布的拟合结果进行了比较,结果表明:采用Lorentz拟合能够得到更好的结果。

