实用化平面超振荡透镜的研究进展
李文丽,虞益挺*
(1.空天微纳系统教育部重点实验室 西北工业大学,陕西 西安 710072;2.陕西省微纳机电系统重点实验室 西北工业大学,陕西 西安 710072)
1 引 言
透镜是光学系统之眼,应用于深空探测、武器装备、生命医学、智能电子等军民生活的方方面面。传统透镜由于存在曲面加工困难、体积大、质量重等问题逐渐被平面超薄透镜替代。随着微纳光学理论及加工技术的迅猛发展,借助厚度仅为数百纳米的微纳结构实现特定距离处聚焦及成像的平面超薄透镜逐渐在智能光电时代大背景下崭露头角[1-5]。
然而,光的波动性使得光学透镜存在衍射极限,传统光学透镜由于远场空间傅立叶高频分量的缺失,聚焦性能受物理衍射极限的限制。1874年,Abbe首次对光学显微镜的分辨率极限进行了定义并将其表示为0.5λ/NA,其中λ为入射光波的波长,NA为光学系统的数值孔径[6]。1924年,Rayleigh提出了非相干成像条件下两点之间的瑞利判据[7],即显微成像系统中恰分辨的两点间最小距离等于光学系统艾里斑的半径(0.61λ/NA)。采用较短的波长入射可在一定程度上提高光学系统的聚焦与成像能力,但其在实际应用场合具有一定的局限性。突破衍射极限实现超分辨光学聚焦与成像,获得尽可能小的衍射聚焦光斑及光场可控的聚焦光场在超分辨光学显微[8-9]、高精密激光加工[10-11]、超高密度数据存储[12-13]、纳米光刻[14-15]、生命医学[16-18]等领域意义深远,科学家们为了实现这一目标已经做出了各种努力。
目前,平面超分辨透镜主要有以下几种类型:一种是利用表面等离子体恢复和放大倏逝波并使其参与成像,如负折射率超透镜[19-22]。由于倏逝波成分束缚在目标物体的表面,这种收集倏逝波的方式都需要成像器件紧贴在物体表面,因此需要高精度的近场操作手段作为保障,难以在准远场及远场实现超分辨。除了这种表面等离子体平面透镜外,研究人员相继提出了另外两种平面超薄透镜:基于波前重构原理的平面超透镜[23-29]和基于超振荡原理的平面超分辨透镜[30-34]。其中,基于波前重构原理的平面透镜,是利用亚波长尺寸单元的结构对电磁波的振幅、相位、偏振等物理量进行调控,在设计上具有较大自由度。然而,这种透镜无法实现远场超分辨聚焦,限制了其在超分辨聚焦与成像领域的应用;此外,由于这类平面透镜的基本构成单元为亚波长尺寸,其批量化、低成本制备也面临重大挑战。与前两类透镜相比,平面超振荡透镜可不借助于亚波长单元尺寸实现远场超越衍射极限的聚焦,并在批量化制备、低成本推广等方面具有明显优势。
本综述将从实用化角度出发,针对平面超振荡透镜的聚焦性能参数、优化设计方法、制备工艺及应用场景等方面的研究现状进行归纳总结,并结合本课题组的理解和认识对该透镜目前存在的问题以及对应的解决办法进行阐述,最后对该研究方向未来发展趋势进行了展望。
2 平面超振荡透镜的性能参数
2.1 超振荡透镜的焦点及其定义
近年来,基于超振荡原理实现远场光学超分辨聚焦与成像引起了国内外研究学者的广泛兴趣。2006年,Berry等人首次证明了在远离点光源的超振荡区域内可实现光场的任意小空间压缩,如图1(a)所示,它无需倏逝波的参与,主要依赖于光场带限函数的局部振荡频率高于其最高傅立叶分量[35]。2007年,英国南安普顿大学的Huang等人利用类Penrose准周期纳米孔结构首次在实验中观察到光学超振荡现象,该结构不仅能用于亚波长聚焦也可用于超分辨成像[36]。2009年,该研究小组利用超振荡原理,通过构造一系列扁长椭球波函数设计了一种通过光场精细干涉实现远场超分辨聚焦的相位、振幅连续调制掩模,在距离掩模表面20λ处获得了大小为0.21λ的光斑[37]。这种平面复振幅结构对当前的微纳加工技术提出了非常严峻的挑战,可以说是一种理论上获得超振荡焦斑的方法。2012年,英国南安普顿大学的Rogers等人利用标量角谱理论设计出一种二元振幅型超振荡透镜,借助共焦扫描成像方式实现了约λ/6的成像分辨率[38]。
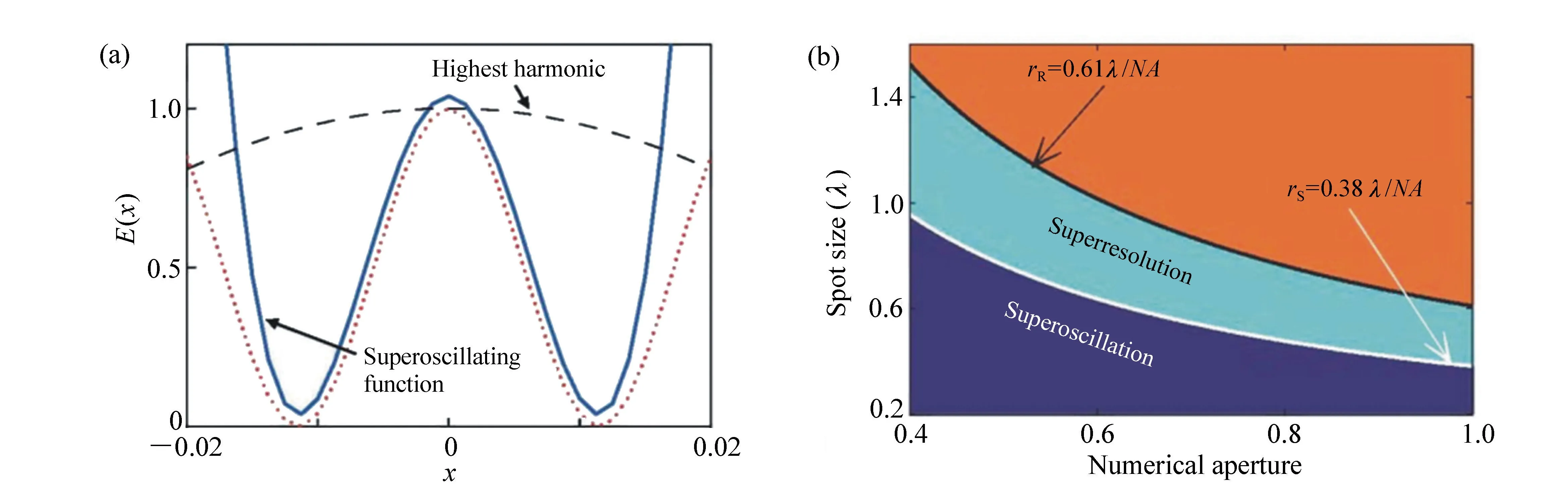
图1 超振荡聚焦产生机理(a)[36]及超衍射极限聚焦判据(b)[39] Fig.1 The mechanism of super-oscillation focusing(a)[36] and the focusing criteria of super-diffraction limit(b)[39]
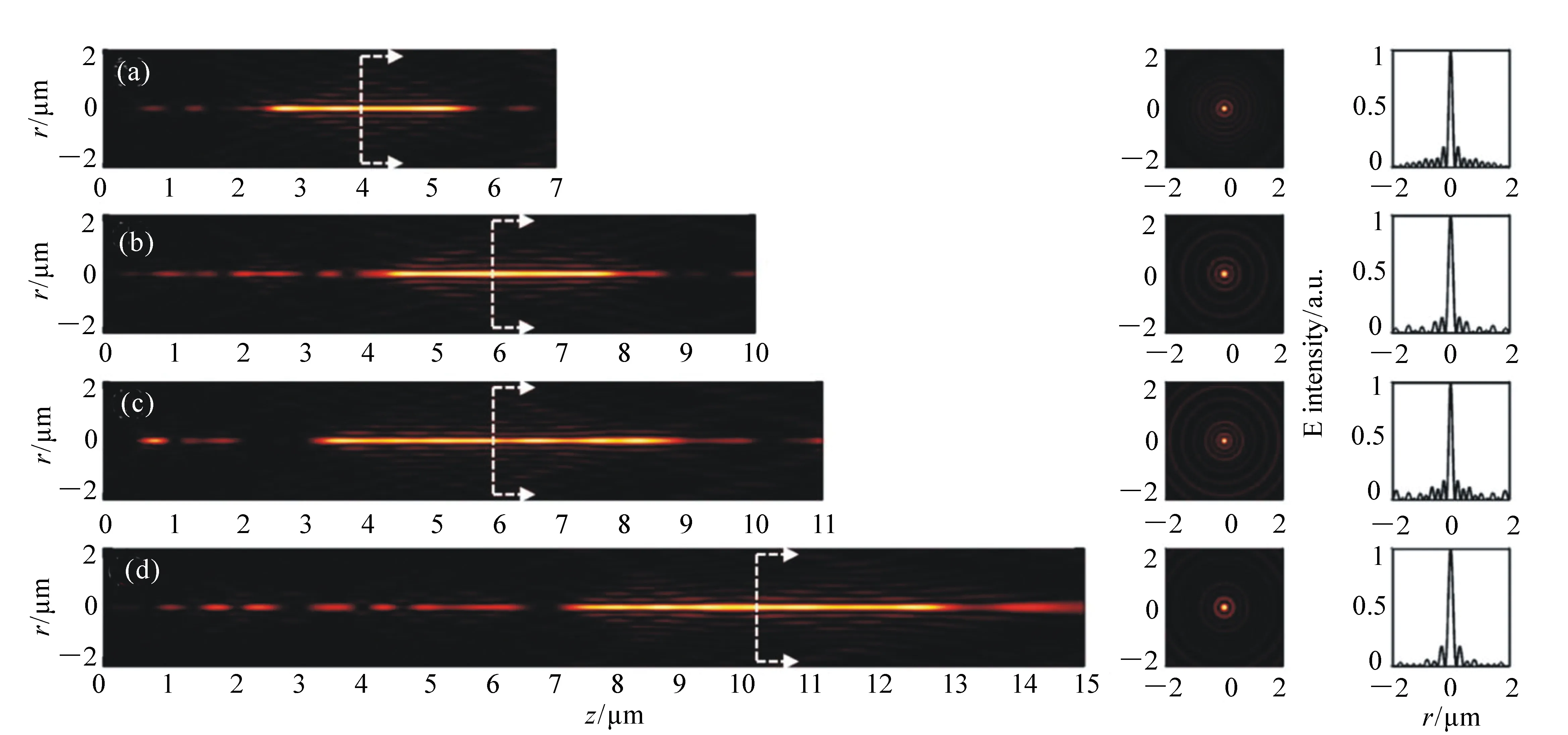
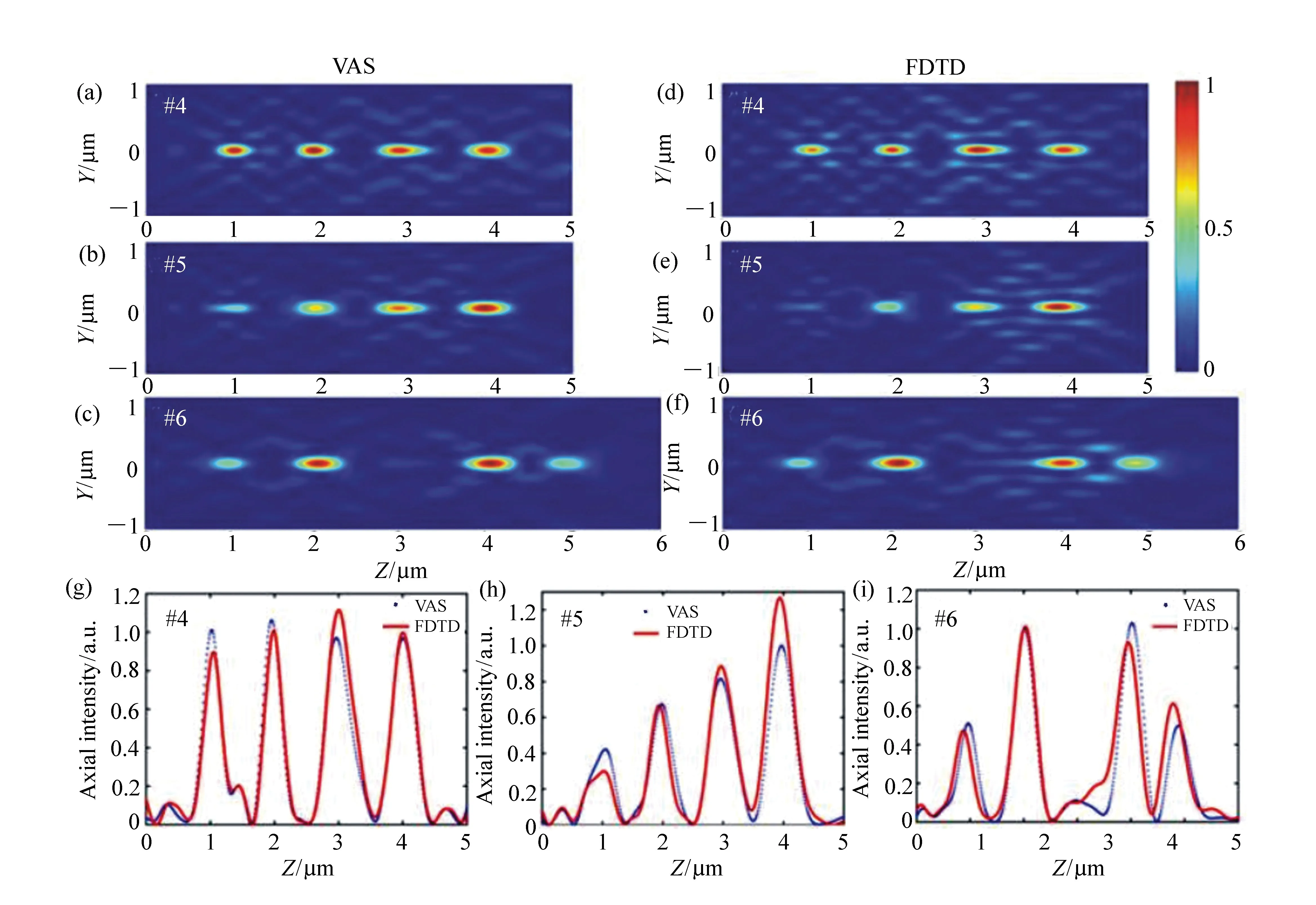
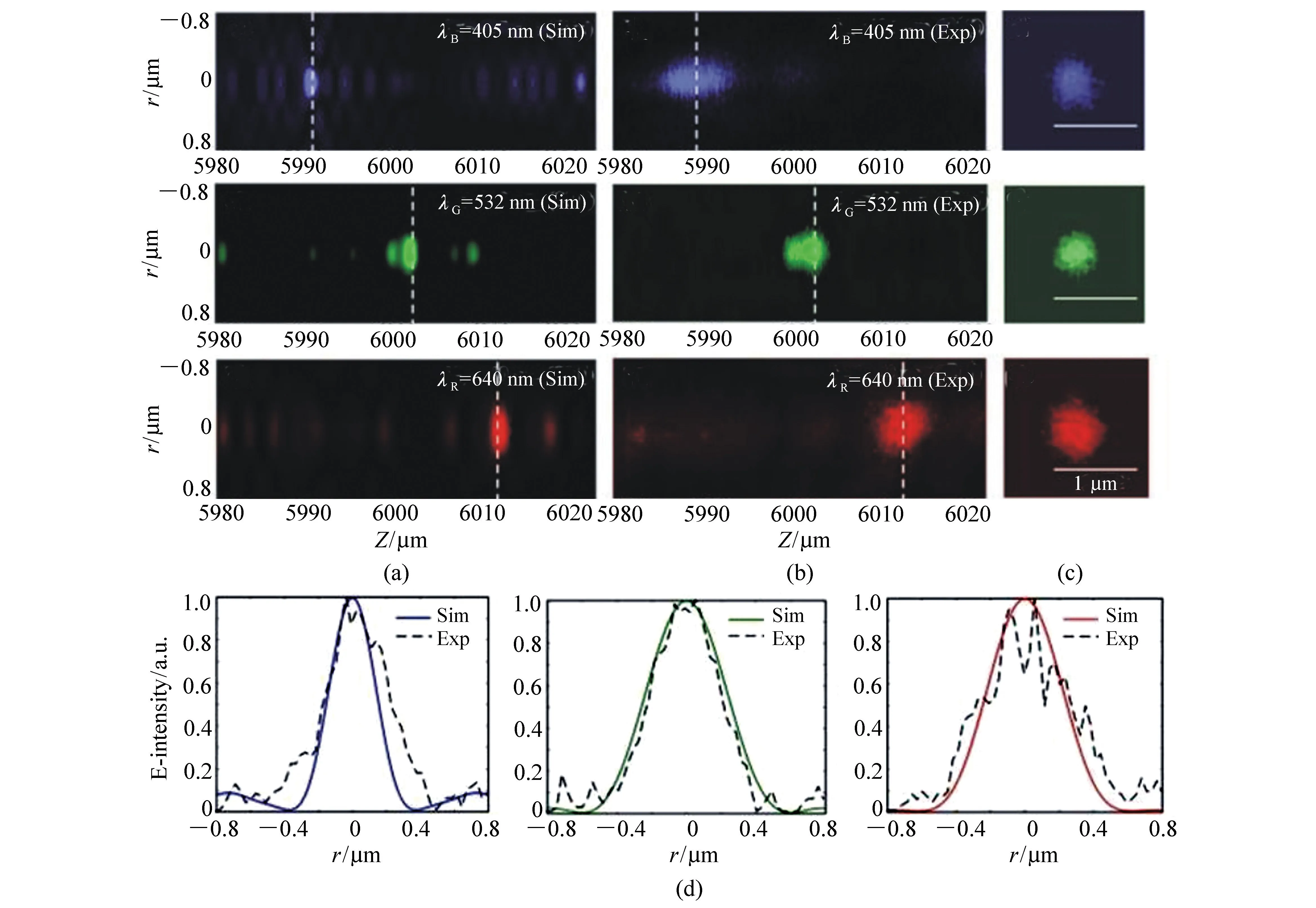
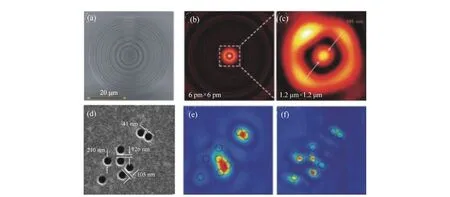
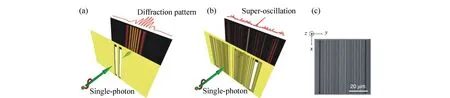
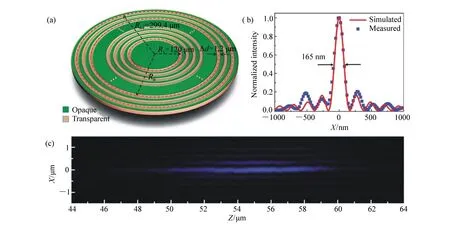
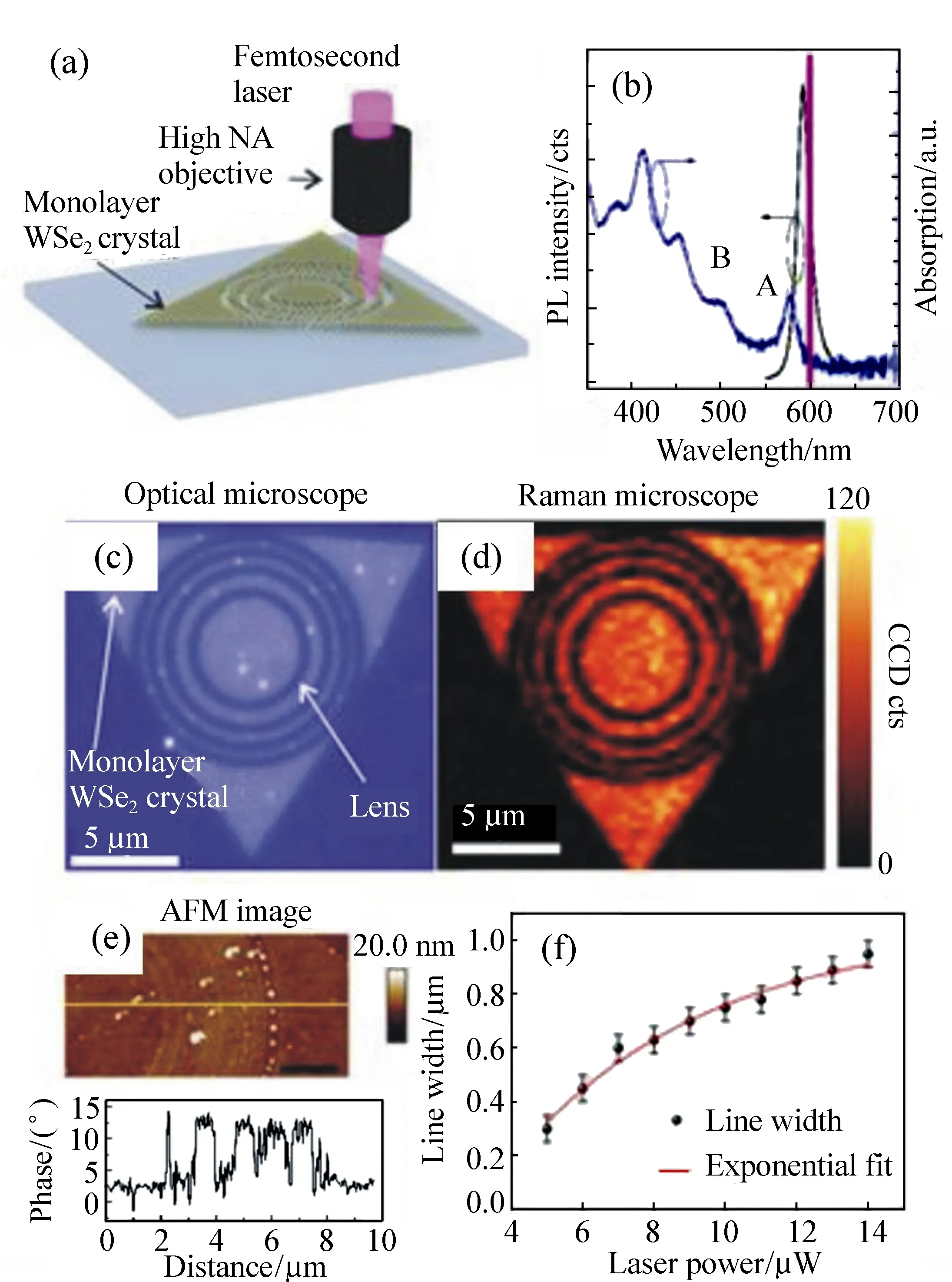
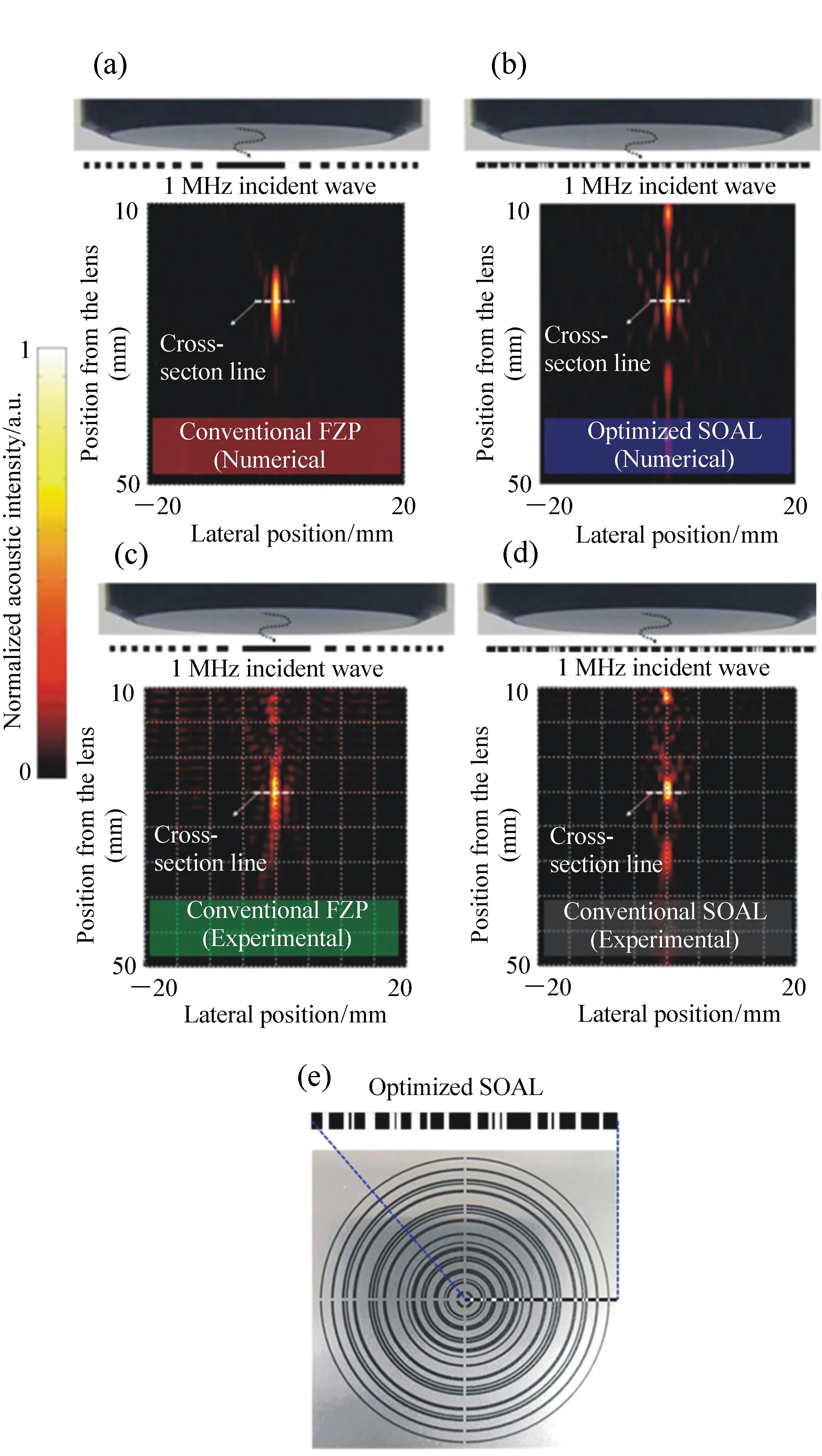
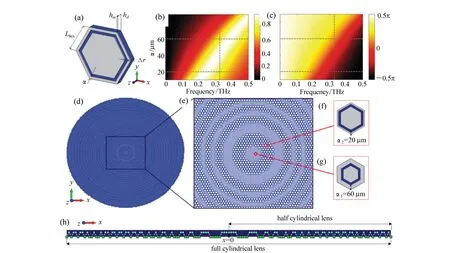
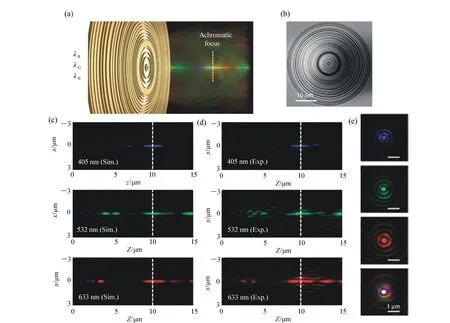
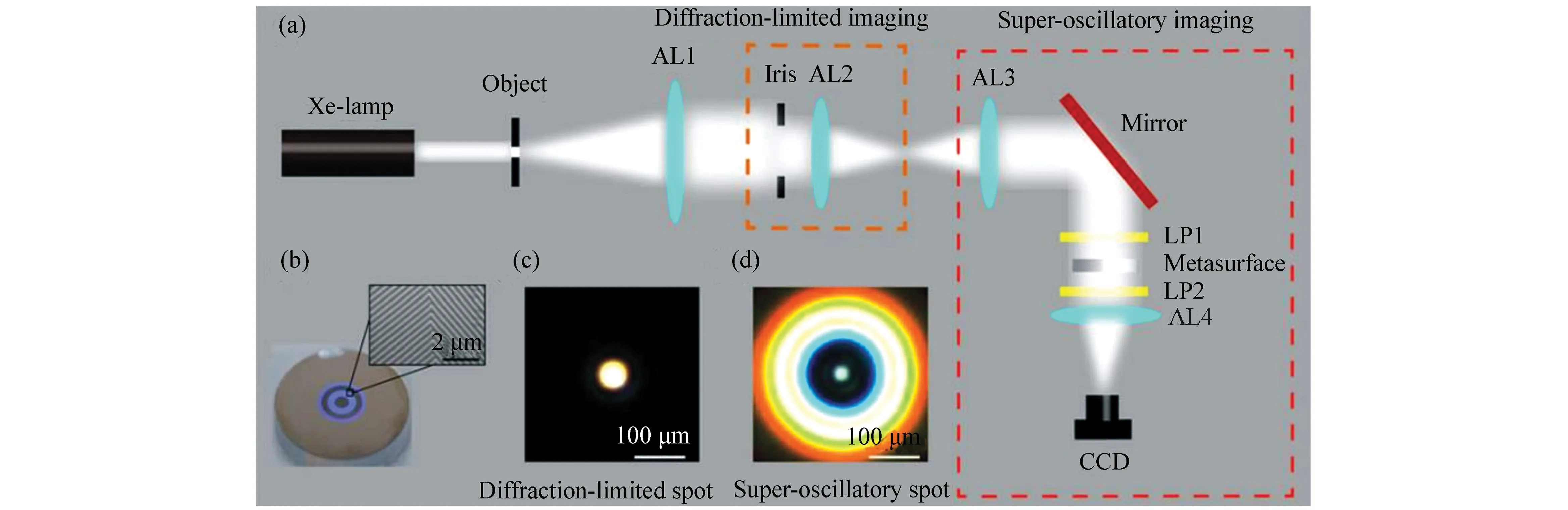
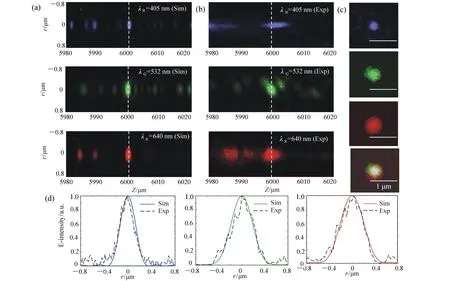
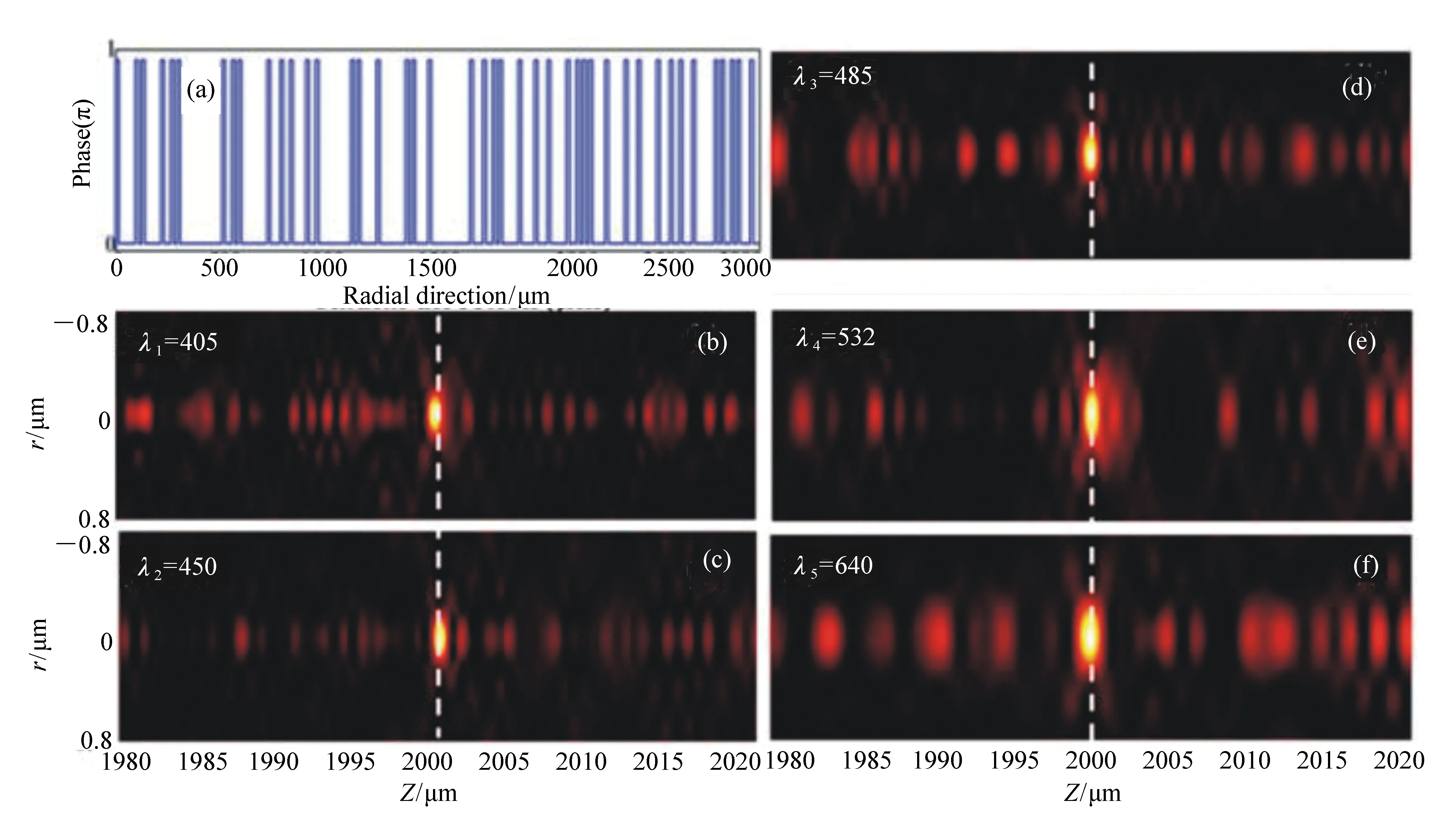
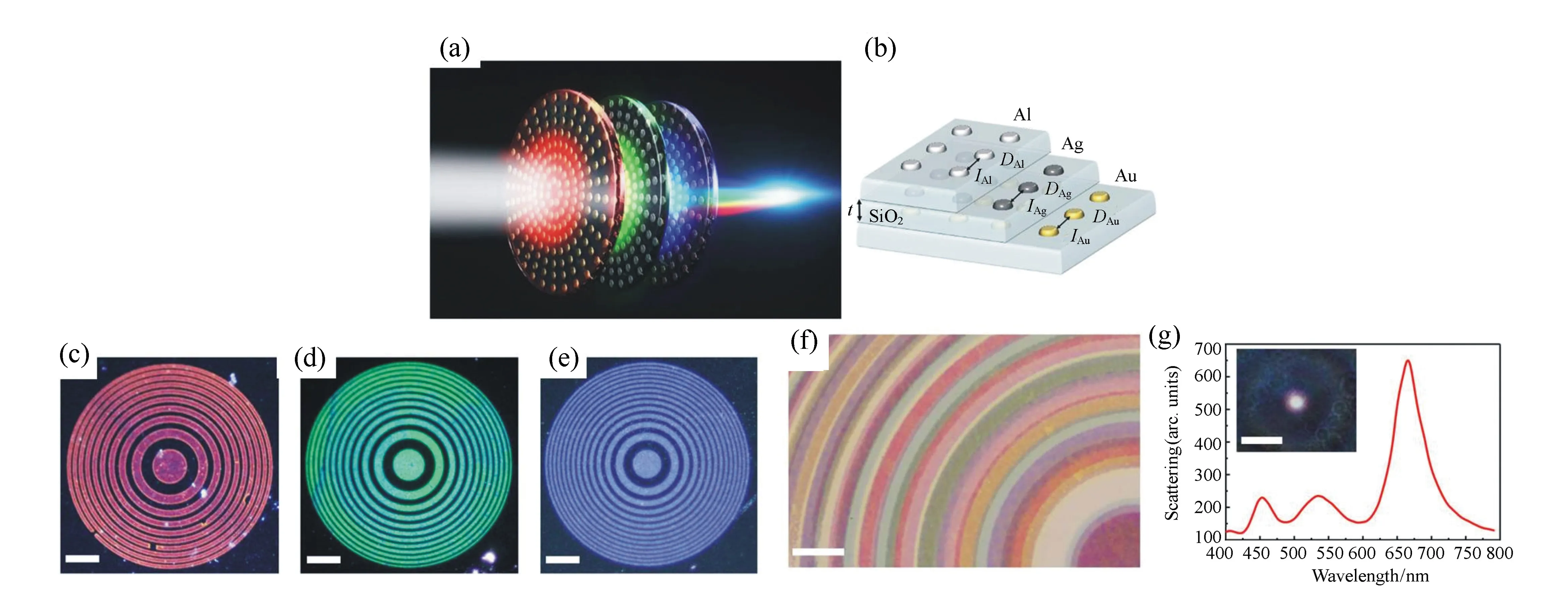
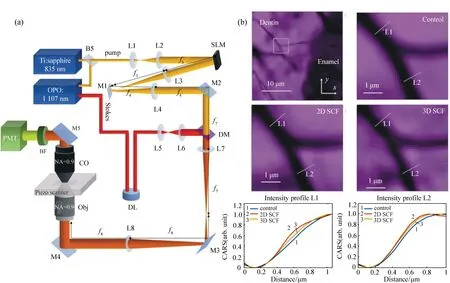
2014年,新加坡国立大学的仇成伟等人,在Berry理论的基础上,提出一个光学系统的聚焦焦斑满足超振荡条件应该具备的3大要素[39]:(1)首先光学系统应为轴对称分布,实现圆形聚焦焦斑;(2)在聚焦平面上一定区域之内,聚焦焦斑的振荡频率要大于该目标平面上的最大傅立叶频谱分量;(3)焦斑要位于r 因此,本论文将以平面超振荡透镜的可控优化设计为出发点,面向实际应用过程中对平面超振荡透镜聚焦性能如焦点尺寸、旁瓣能量、焦深等提出的要求为导向展开相关讨论。 在透镜的实际使用过程中,焦深作为一项重要的性能参数,扮演着极其重要的角色,当观察具有一定厚度的样品时需要一定长度的焦深才能保证样品在不同深度处的图像都能看清。并且,应用场景不同,透镜所需要的焦深也不同。传统透镜的焦深与其数值孔径有关,当数值孔径越大时焦深越短,在透镜设计时可根据具体的数值孔径计算得到焦深[41-42]。与传统透镜数值孔径与焦深存在固定的关系不同,平面超振荡透镜由于具有灵活的光场可控性,在光轴上可通过定义优化参数在一定长度内实现焦深调制。通过在优化过程中定义具体的参数以及设计相关约束将高数值孔径的平面超振荡透镜的焦深设计为数十倍波长[43-48],研究人员将这类在光轴方向具有长焦深且光强均匀性好、一致性强的光斑形式定义为光针。2016年,本课题组通过建立一种多目标多约束优化模型,设计了数值孔径接近1的平面超振荡透镜[49],通过调控优化参数得到在光轴方向均匀性较好、焦深长度约12倍波长的光针,如图2(彩图见期刊电子版)所示,该设计结果得到了国内外同行的广泛关注。此外,研究人员还发现这种光针具有无衍射特性[50-51],这一特征使其在深度超分辨成像[52]、粒子操纵[53]及生物成像[54]方面具有潜在应用。 图2 平面超振荡透镜光针聚焦性能优化结果[49] Fig.2 The optimized results of focusing performance of needle-like SOLs[49] 另一方面,由于平面超振荡透镜在轴向光场调制上具有较大的灵活性,2017年,本课题组通过建立多焦点多约束优化模型设计了一种多焦点平面超振荡透镜[55],经过合理设置优化参数及约束模型,可对轴向焦点个数、焦点强度进行任意控制,如图3(彩图见期刊电子版)所示。结果显示设计和仿真中的焦点尺寸均突破了衍射极限。这种通过优化建模实现轴向多焦点透镜的设计方法大大简化了传统透镜中构建轴向多焦点光场的设计复杂度[56-58],并且通过精细复杂的光场调制可获得远场甚至超远场处突破衍射极限的聚焦焦点。这种平面多焦点超振荡透镜在并行粒子操纵[59]方面具有一定的应用价值。 图3 多焦点平面超振荡透镜聚焦性能优化结果[55] Fig.3 The optimized results of focusing performance of planar multifocal SOLs[55] 图4 平面超振荡透镜的普遍色散规律[60] Fig.4 The common dispersive rules of planar SOLs[60] 此外,受多焦点透镜设计的启发,本课题组就超振荡透镜的色散进行了可控优化。平面超振荡透镜作为一种衍射透镜,其色散规律与传统的衍射透镜一致,即长波长对应短焦距,如图4(彩图见期刊电子版)所示。通过建立优化控制模型,本课题组设计了一种色散可定制的平面超振荡透镜[60],巧妙地将长波长的焦点设计在距离透镜后表面最远距离处,将短波长的焦点设计在距离透镜后表面最近距离处,并通过搭建实验测试系统表征了所设计透镜的聚焦性能,如图5(彩图见期刊电子版)所示。结果表明,所设计的色散定制型平面超振荡透镜聚焦性能设计结果与实验结果具有较好的一致性,均在约12 000λ处获得了超衍射极限的聚焦焦点。这种色散可定制超振荡透镜的设计为其在光通讯[61]、数字全息[62]、便携式光纤光谱仪[63]等领域的应用提供了可能性。此外,这种设计思路为单个超振荡透镜实现多个波长不同功能调制提供了参考。 透镜作为一种重要的成像工具,在实际应用过程中,视场也是表征其性能优劣的一个重要参数。2018年,英国南安普顿大学的Rogers等人对超振荡透镜的视场问题进行了讨论[64],他们指出:平面超振荡透镜的视场大小与透镜的焦点尺寸有关,当焦点尺寸被控制的极小时,往往伴随着高能量的旁瓣,且这时旁瓣能量会大于主瓣的能量,这在实际应用中是非常不利的。因此,通过优化控制得到较低的旁瓣能量,从而扩大超振荡透镜的视场是十分必要的。目前有两种减小旁瓣能量的方式,一种是通过在共聚焦显微成像光路中引入微小孔径光阑,通过光阑将不需要的旁瓣能量过滤掉,从而实现主焦点的扫描成像。另一方面,也可在中心主焦点与第一旁瓣之间叠加多个强度为零的点来扩大超振荡透镜的视场[39,65]。需要注意的是,在所控制超振荡透镜的焦点尽可能小的同时要保证最大的光轴强度,使其在实际成像、高分辨数据存储等领域中更好地发挥作用。 图5 色散定制的平面超振荡透镜[60]. (a)消色差超振荡透镜的优化设计结果:λB=405 nm, λG=532 nm, λR=640 nm;(b)实验表征结果:λB=405 nm, λG=532 nm, λR=640 nm; (c)焦平面实验表征结果:λB=405 nm, λG=532 nm, λR=640 nm;(d)半高宽曲线实验仿真对比:λB=405 nm, λG=532 nm, λR=640 nm[60] Fig.5 The achromatic-customized planar SOLs[60]. (a)The optimized results of λB=405 nm, λG=532 nm, λR=640 nm; (b)experimental results of λB=405 nm, λG=532 nm, λR=640 nm; (c)experimentally registered intensity patterns in the transverse focal plane for λB=405 nm, for λG=532 nm, for λR=640 nm; (d)comparison of experimental and simulation results of the full width at half maximum(FWHM) for λB=405 nm, λG=532 nm and λR=640 nm[60] 任何事物都具有两面性。高能量的旁瓣在精确合理的控制下也可作为一种面包圈光场在受激发射损耗成像[66-67]、粒子操纵[68]等领域产生有价值的应用。研究人员通过将入射光偏振态改为角向偏振光或径向偏振光[69-70]并通过设计相关参数得到了突破衍射极限的面包圈光场,这种面包圈光场由于携带轨道角动量,可对纳米颗粒物进行微机械操纵。不难发现,超振荡透镜在优化约束的过程中焦点大小、旁瓣大小以及能量强度这3个因素属于相互冲突、相互矛盾的关系。在超振荡透镜的实际应用场合中,应权衡考量这三者的关系。 超振荡透镜聚焦效率方面,现有的超振荡透镜主要有二元振幅型、二元相位型以及振幅和相位同时调制3种类型。2012年,英国南安普顿大学Rogers等利用标量角谱理论设计出一种二元振幅型超振荡透镜,并借助共聚焦扫描成像方式实现了约λ/6的成像分辨率[38],如图6所示(彩图见期刊电子版)。该研究小组同时指出所研制的超振荡透镜焦点处光学效率的实测值约为10%。2016年,Yuan[71]等人进一步研究发现,超振荡现象在单光子激发状态下同样存在,成功验证了量子超振荡效应,如图7(彩图见期刊电子版)所示,但其本质上仍为一种二元振幅型透镜,其聚焦效率为16%。可以看到,获取小于超振荡标准的焦点尺寸是以牺牲聚焦焦斑能量强度为代价的,同时伴随着高能量的旁瓣,极大地影响了透镜的应用。同年,新加坡国立大学仇成伟课题组设计了一种焦点尺寸介于超振荡标准与瑞利衍射极限标准之间的二元振幅型超振荡透镜,并将其命名为超临界透镜[40],如图8(彩图见期刊电子版)所示,并通过实验表征测得所设计透镜的聚焦效率约为16.2%。不难看出,研究人员在设计和实验表征上实现了从平面超振荡透镜到平面超临界透镜的跨越,但都是基于二元振幅型透镜设计的。这类平面超振荡透镜聚焦效率最高也仅为16%,对其在超分辨聚焦与成像、高密度数据存储等领域的应用提出了重大挑战。 图6 (a)二元振幅型平面超振荡透镜的电镜图;(b)计算焦平面电场分布;(c)实测焦平面电场分布;(d)金属薄膜上制备的纳米孔;(e)传统透镜未能分辨的纳米孔图像;(f)经超振荡透镜分辨的纳米孔图像[38] Fig.6 (a)Scanning electron microscope(SEM) image of the binary amplitude type planar SOLs; (b)electric field distribution of calculated focal plane of the SOLs; (c)electric field distribution of actual focal plane; (d)SEM image of a cluster of nanoholes in a metal film; (e)image of the cluster is not resolved with a conventional lens; (f)image of the cluster resolved by super-oscillatory lenses[38] 图7 单光子的量子超振荡。(a)观察杨氏双缝实验中的量子干涉现象;(b)一维超振荡透镜中的量子振荡效应;(c)一维超振荡透镜的电镜图[71] Fig.7 Quantum super-oscillation of single photon. (a)Observation of quantum interference in the Young double-slit experiment; (b)quantum super-oscillations of one-dimensional SOLs; (c)electron micrograph of the mask[71] 图8 二元振幅型超临界透镜。(a)405 nm 超临界透镜构型;(b)聚焦强度分布实验结果与仿真结果对比;(c)轴向电场强度实验表征结果[40] Fig.8 The binary amplitude-type supercritical lens. (a)Configuration of the 405 nm supercritical lens; (b)comparison of the focusing intensity distributions between the simulated and experimental results; (c)axial measured intensity profile along the propagation distance[40] 为了减小振幅型超振荡透镜透过率低导致参与透镜聚焦的能量大幅损失的问题,研究人员又把目光转向了相位型超振荡器件。不同于平面二元金属振幅型超振荡透镜,相位型超振荡透镜可通过对透光介质进行刻蚀产生相对相位差进而对入射光场进行调制来获得超振荡聚焦焦斑。与振幅型透镜相比,相位型超振荡透镜的优点是可在保持相对较好的超分辨聚焦性能的同时又大幅提高了入射光场的能量利用率,因此在实际应用过程中更具优势。2014年,仇成伟课题组提出一种利用无优化方式构建二元相位掩模对线偏振和圆偏振光实现远场的超振荡调制[64],但在传统光学材料上精确制备这种二元相位型平面透镜存在较大的工艺挑战。2015年,西安交通大学刘涛等人针对相位型超振荡透镜进行优化设计[72],获得了约为0.39λ的光斑尺寸,焦距为10.74 μm,结果表明:相位型超振荡透镜中心焦斑的强度是相同条件下振幅型超振荡透镜焦斑强度的5.8倍,但这一工作只停留在计算仿真阶段。2016年,重庆大学陈刚课题组连续报道了两个基于二值相位(0,π)的调控角偏振及圆偏振实现超振荡聚焦的透镜案例[73-74],研究表明这类透镜的聚焦效率最高约为40%[75-76]。然而因特征尺寸为亚波长量级需要通过电子束曝光工艺完成透镜制作,故存在高成本问题。可以看到,现有的二元相位型平面超振荡透镜的聚焦效率最高仅为40%,为了更好地将这种透镜推广到实际应用中,需开展有关高聚焦效率的平面超振荡透镜的研究。 二维材料由于其可在原子层厚度的基底上获得高折射率,逐渐成为光电研究领域的新宠,许多光学透镜方向的研究组也逐渐对二维材料展开研究。2016年,澳大利亚国立大学的一个研究组基于二硫化钼这种二维材料,设计了世界上最小最薄的传统折射式透镜[77]。这项研究为二维材料与光学透镜结合提供了解决思路。2018年,澳大利亚斯温伯恩理工大学的研究人员联合新加坡国立大学的研究人员一起利用单层二硒化钨设计并制备了一种二元振幅型平面超振荡透镜[78],如图9所示(彩图见期刊电子版),其聚焦效率为31%,较之前基于金属薄膜材料的二元振幅型平面超振荡透镜的聚焦效率得到了大幅度提升。随后,研究人员又对基于二维材料的平面超透镜进行了研究[79],发现这种借助二维材料超薄厚度但折射率比传统材料高的光学性质可用来提高透镜的聚焦效率。因此,未来可借助二维材料的高折射率及原子层厚度来设计制备高效率的相位型平面超振荡透镜。 图9 二硒化钨材料制成的振幅型平面超振荡透镜。(a)单层二硒化钨透镜的飞秒激光加工过程;(b)单层二硒化钨晶体的吸收和光致发光谱;(c)制备的单层二硒化钨透镜的反射图;(d)所制备透镜的共焦拉曼图;(e)制备的二硒化钨透镜的原子力显微镜图;(f)入射光功率与线宽的函数关系[78] Fig.9 The amplitude-type SOL made from WSe2. (a)Schematic view of the femtosecond laser fabrication process of monolayer WSe2 lens; (b)absorption and photoluminescence spectra of the monolayer WSe2 crystal; (c)reflective optical microscopic image of a fabricated monolayer WSe2 lens; (d)confocal Raman microscopic intensity imaging of a fabricated monolayer WSe2 lens; (e)atomic force microscope(AFM) image of a fabricated monolayer WSe2 lens; (f)line width as a function of the incident laser power[78] 图10 超声超振荡透镜。 (a)传统菲涅尔透镜的声场强度数值计算结果;(b)优化设计的超振荡声学透镜声场强度分布;(c)实验测试的菲涅尔透镜声场强度分布;(d)实验测试的超振荡透镜声场强度分布;(e)制备的超振荡声学透镜[80] Fig.10 The ultrasonic SOLs. (a,b)Numerically calculated acoustic intensity fields by the conventional Fresnel zone plate (FZP) lens (left panel, a) and the optimized super-oscillatory acoustic lens (SOAL), (right panel, b); (c,d)experimentally measured acoustic intensity field radiated by the conventional FZP lens (left panel, c) and the optimized SOAL (right panel, d); (e)fabricated optimized SOAL with a single layer[80] 在透镜的设计和使用过程中,工作谱段和带宽是在设计之初就必须直接考虑的参数,且它们尤为重要。常见的超振荡透镜主要是面向可见光波段进行优化设计的,随着人工智能时代对光电器件的要求日益严苛,超振荡透镜的工作谱段也逐渐从可见光波段向近红外、红外甚至超声波段及太赫兹波段发展。2018年,韩国标准和科学研究院的科研人员设计了一种超声超振荡透镜[80],如图10所示(彩图见期刊电子版)。所设计的超声超振荡透镜在水介质中实现了波长为1 MHz的超声波聚焦。这项研究为超振荡透镜在声学显微镜中的应用提供了可能。随着研究的深入,平面超振荡透镜的设计将面向近红外、红外波段的应用,在这些波段,透镜的线宽将不再是数百纳米。这种大线宽的特征尺寸将会为这类透镜的批量化、低成本制备提供有利条件。 同年,英国纽卡斯尔大学的研究组设计了一种工作在太赫兹波段的平面超振荡透镜[81],如图11(彩图见期刊电子版)所示,所设计的平面超振荡透镜基本构成单元为六角形晶胞单元,通过优化设计实现了0.46λ的聚焦焦斑。这种设计可为太赫兹波段超分辨成像提供更多的可能性。 图11 太赫兹波段的超振荡透镜。 (a)六边形单元几何参数;晶胞单元的透射系数归一化的强度(b)和相位(c)分布;透镜的整体效果(d)及局部放大效果图(e);(f,g)晶胞单元的奇数偶数区域;(h)所设计的圆柱透镜的晶胞单元分布[81] Fig.11 The SOLs at the Terahertz wavelengths. (a) Hexagonal unit cell proposed along with its geometrical parameters; (b)normalized magnitude and (c)phase (in radians) maps of the transmission coefficient of the unit cell as a function of the parameter α and frequency; (d)full metalens schematic and (e) zoomed view of the metalens central zones; (f,g)unit cells of the even and odd zones, respectively; (h)unit cell distribution of the designed cylindrical lens[81] 从2009年提出超振荡透镜的概念以来,现有的平面超振荡透镜主要是面向可见光波段中的某个单一波长进行设计的。与传统透镜一样,这种透镜也面临着色散问题。2015年,英国南安普顿大学Zheludev课题组通过焦深重叠的办法设计了一种可在三波长入射下同时工作的消色差平面超振荡透镜[82],如图12所示(彩图见期刊电子版),但这种方法只是通过设计重叠区域强制使若干波长在需要的工作距离处得到消色差聚焦。2018年,中国科学院光电技术研究所的罗先刚课题组借鉴超表面结构单元在宽波段下能够响应的工作原理,设计了一种基于Pancharatnam-Berry相位的宽波段超振荡超表面透镜[83],并搭建了成像实验平台,如图13所示,验证了所设计透镜的宽波段成像效果,但这种透镜的构成单元仍为亚波长尺寸,在大尺寸、低成本推广方面仍存在挑战。为了更快速、有效地设计一种大尺寸、可批量化制备的消色差平面超振荡透镜,本课题组也建立了一种多目标无约束优化模型直接对三波长入射的平面超振荡透镜进行了控制设计,并开展了相关实验表征[60],如图14所示(彩图见期刊电子版),结果表明所设计的3个波长在同一焦距处实现了消色差的聚焦,且焦点均在12 000λ的超远场处突破了衍射极限。与此同时,为了验证算法的有效性,还设计了一种同时实现5个波长消色差的平面超振荡透镜,并得到了预期的效果,如图15所示(彩图见期刊电子版)。这种方法为更多波长实现消色差提供了可能性。 图12 利用焦深重叠办法实现的消色差超振荡透镜。 (a)消色差超振荡透镜在3个波长处聚焦,红(λR=633 nm),绿(λG=532 nm),蓝(λB=405 nm);(b)制备的超振荡透镜的电镜图;透镜在xz面的电场强度分布(c)仿真及(d)实验表征结果;(e)横向焦平面的电场强度图(从上至下分别为对应λB、λG、λR及3个波长合成的结果)[82] Fig.12 The achromatic SOLs achieved through the focal depths overlapped. (a)Apochromatic SOL focuses simultaneously at three different wavelengths, red(λR=633 nm), green(λG=532 nm), and blue(λB=405 nm); (b)SEM micrograph of the fabricated mask with diameter of 40 μm, and working distance of 10 μm; simulated (c) and experimental (d) diffraction patterns in the xz cross-section; (e)experimentally registered intensity patterns in the transverse focal plane(from top to bottom are for λB, λG, λR, and for RGB wavelengths by simultaneously switching on the three channels)[82] 图13 基于P-B相位的连续宽波段超振荡超透镜。(a)实验装置图;(b)制备的超表面结构;(c)衍射受限的直径为20 μm的纳米孔成像效果;(d)直径为20 μm的纳米孔超振荡成像效果[83] Fig.13 Continuous broadband SOLs based on P-B phase. (a)Schematic of experimental setup; (b)proposed metasurface; (c)diffraction-limited image of a hole with a diameter of 20 μm; (d)superoscillatory image of a hole with a diameter of 20 μm[83] 图14 通过优化方法直接设计的消色差超振荡透镜.(a)消色差超振荡透镜的优化设计结果:λB=405 nm, λG=532 nm, λR=640 nm;(b)实验表征结果:λB=405 nm, λG=532 nm, λR=640 nm; (c)焦平面实验表征结果:λB=405 nm, λG=532 nm, λR=640 nm及三通道拟合结果;(d)半高宽曲线实验仿真对比:λB=405 nm, λG=532 nm, λR=640 nm[60] Fig.14 The achromatic SOLs designed by optimization. (a)The optimized results of λB=405 nm, λG=532 nm, λR=640 nm; (b)the experimental results of λB=405 nm, λG=532 nm, λR=640 nm; (c)experimentally registered intensity patterns in the transverse focal plane for λB=405 nm, for λG=532 nm, for λR=640 nm, and for RGB wavelengths by simultaneously switching on the three channels; (d)comparison of experimental and simulation results of the full width at half maximum(FWHM) for λB=405 nm, λG=532 nm and λR=640 nm[60] 图15 五波长消色差超振荡透镜。 (a)消色差超振荡透镜相位分布;XZ面电场分布(b)λ1=405 nm;(c)λ2=450 nm, (d)λ3=485 nm;(e)λ4=532 nm;(f)λ5=640 nm Fig.15 Achromatic SOLs for five wavelengths. (a)The phase distribution of the achromatic SOLs; the electric field contours in the XZ cross-section at (b)λ1=405 nm; (c)λ2=450 nm; (d)λ3=485 nm; (e)λ4=532 nm; and (f)λ5=640 nm 图16 复合菲涅尔多层消色差透镜。(a)透镜的艺术效果图;(b)多层结构的说明图;(c~e)单层透镜的暗场图,不同元素根据红,绿,蓝3个颜色设计的;(f)三层透镜的明场透射图;(g)白光照明的光谱图及焦点强度分布[84] Fig.16 Composite multilayered achromatic Fresnel lens. (a)Artist′s view of the three-layer lens; (b)schematic illustration of the layered structure; (c~e)dark-field images of the single-layer lens elements. The different elements are designed to focus red, green or blue to 1 mm focal distance along the optical axis(scale bar, 35 mm); (f)bright-field transmission image of the three-layer lens; (g)spectrum taken under white light illumination at the focal spot, revealing the RGB components[84] 连续宽波段聚焦将成为平面超振荡透镜设计优化的一大趋势。除了在算法上进行多波长设计之外,通过多层结构进行设计也是一个新兴方向。多层结构较原有的单层结构在设计参数上具有更大的自由度,并可在结构形式和优化目标两方面同时做改进。2017年,以色列特拉维夫大学的研究人员提出了一种组合菲涅尔透镜的方法以实现三波长消色差的设计[84],如图16所示(彩图见期刊电子版),通过材料对波长的选择特性,实现特定波长的光聚焦。2018年,美国范德堡大学的研究人员提出一种考虑透镜间无串扰的多层消色差透镜[85],如图17所示(彩图见期刊电子版),通过将前一层透镜的出射光场作为下一层结构的入射光场,并结合菲涅尔衍射理论进行优化设计,实现了多层结构消色差超表面的设计,这种方法为多层平面超振荡透镜实现宽波段聚焦提供了新思路。 图17 多层无串扰消色差超透镜。(a)加工工艺步骤流程图;(b)旋涂PDMS之前的硅纳米柱的扫描电镜图;(c)定位双层透镜的光学显微镜图像;(d)双层结构定位用对准标记显微图像;(e)两种波长下,当定位误差δ分别为1、3、6 μm时的仿真轴向强度图[85] Fig.17 Non-crosstalk multilayered achromatic SOL. (a)Schematic of the fabrication steps; (b)SEM of Si nanoposts before polydimethylsiloxane (PDMS) spin coating; (c)optical microscope image of the aligned metalens doublet; (d)optical microscope (20× objective) image of the alignment marks from the two layers along with a schematic of cross section; (e)simulated axial intensity profiles of the metalens doublet with the misalignment δ of 1, 3 and 6 μm at the two wavelengths[85] 超振荡透镜优化设计,最早是基于标量衍射理论对超分辨光瞳滤波器进行研究的[86-87]。2006年,英国布里斯托大学的Berry等人[35]经过一系列的理论推导并从频域角度进行分析,借助光学微纳结构对传输光场的干涉现象精密调制,在远场实现了超越衍射极限的光学聚焦焦斑。2009年,英国南安普顿大学的Zheludev研究团队[37]提出了基于有限带宽函数的超振荡光场构建方法,采用正交椭圆球面函数集的带宽有限特性和局域展开特性,定义出需要的超分辨光场分布,从而逆推透镜的透射函数。这种方法设计出的透镜相位分布具有负透镜特征,与传统聚焦成像器件存在较大差异。 由于超振荡透镜本质上是一种经过优化设计的衍射光学元件,其聚焦特性完全可通过各种衍射理论和优化算法,对各同心环带的位置和宽度参数进行优化设计来实现。现有的衍射理论主要包括标量衍射理论和矢量衍射理论。对于低数值孔径的平面透镜,可采用标量衍射理论来对透镜后表面的衍射场分布进行计算。然而,标量衍射理论忽略了入射光的偏振特性,其聚焦光场也无法体现出电场的偏振特性。但在实际传播过程中,透镜后光场分布可根据入射光偏振态的变化而发生改变,尤其对于高数值孔径透镜,标量衍射理论已经在很多文献报道中证明不再适用[88-90]。目前,平面超振荡透镜的结构主要分最优化算法和无优化直接计算两种方式。2012年,N. I. Zheludev研究团队首次在角谱理论框架下用粒子群优化算法设计了一种直径为40 μm、焦距为10.3 μm的二元振幅型超振荡透镜[38],并对其成像性能进行了表征。接着,研究人员用粒子群优化方法设计了一系列平面超振荡透镜并进行了相关性能表征[43,82,91],获得了与设计相匹配的结果,但存在设计方法复杂的问题。2013年,哈尔滨工业大学刘涛等人以径向偏振光作为入射光源,以折射率n=1.515的松柏油作为出射介质,利用矢量衍射理论和遗传算法对振幅型超振荡掩模进行优化[33]。该方法将超振荡透镜的研究推广到矢量领域,但是在设计过程中未能实现对焦距和焦深等参数的有效控制。为了更好地利用优化算法实现对超振荡透镜后聚焦光场的调制,本课题组先后建立了多目标多约束优化设计模型对平面超振荡透镜后光针[49]以及多焦点[55]光场进行了设计,如图2、图3所示。然而,这种多目标多约束优化设计模型存在收敛速度慢且常常出现结果发散的情况。2018年,本课题组在原有多目标多约束的优化设计基础上提出了一种多目标无约束的超振荡透镜光场可控通用优化模型,通过引入惩罚函数项将约束优化问题转化为无约束优化问题[60],所建立的光场优化设计通用模型可对平面超振荡透镜后表面光场进行灵活可控设计。 随着计算机科学的飞速发展,平面超振荡透镜的优化设计有望与机器学习、人工神经网络等技术相结合,以期高效、快速地完成多目标优化中大尺寸、多功能平面超振荡透镜的设计。 超振荡透镜的结构形式从2007年最早的Penrose准周期纳米孔结构发展到目前常见的同心圆环结构,经历了亚波长单元特征尺寸到若干倍亚波长特征尺寸的变化,随之而来的是加工工艺也发生了改变,其发展历程如图18所示。可以看到,现有的平面超振荡透镜主要是基于聚焦离子束刻蚀[32,36,38,82,92-93]和电子束曝光[70,71,94-95]工艺制备的,存在加工成本高、耗时且难以实现大尺寸平面超振荡透镜的制作。 图18 平面超振荡透镜加工工艺发展过程[60] Fig.18 Development process of the fabrication process on planar SOLs[60] 随着集成电路制造技术及微纳加工工艺的发展,平面超振荡透镜的并行制作工艺也逐渐成为主流发展趋势。2017年,新加坡国立大学仇成伟课题组将平面超振荡透镜的特征尺寸提高到1.2 μm,替代了之前的亚波长特征尺寸的平面超振荡透镜。然而,这种基于深紫外光刻工艺制备的平面超振荡透镜的直径仅为数百微米,与现有成熟的光学元器件集成存在挑战。2018年,南京信息科技大学NI H B等人[96]提出利用激光直写工艺实现非亚波长特征尺寸平面超振荡透镜的制备,但这种工艺制备大尺寸平面超振荡透镜时需利用拼接的办法实现,存在较大的定位误差。2018年,本课题组设计了最小线宽为30 μm、直径为12 mm的平面超振荡透镜,针对这种介质型超振荡透镜提出了一套基于传统光刻工艺的圆片级制备流程,如图19所示,所制备的圆片级平面超振荡透镜如图20所示,其实验表征与仿真较为一致。 图19 平面超振荡透镜圆片级制备工艺[60] Fig.19 Wafer-level fabrication process of planar SOLs[60] 图20 圆片级平面超振荡透镜加工结果[60] Fig.20 Fabrication results of wafer-level planar SOLs[60] 超振荡透镜应用方面,主要体现在远场非标记超分辨显微成像、超高密度数据存储两大领域。现有的平面超振荡透镜的成像方式主要是借助共聚焦显微成像平台实现扫描成像的方式,最具代表性的是2012年英国南安普顿大学Zheleduv研究团队的工作,他们在改装后的尼康共聚焦显微成像系统上对直径为40 μm、焦距为10.6 μm的平面超振荡透镜进行成像实验,实现了油浸环境下λ/6的超衍射极限分辨率成像[38],但这种成像存在焦深短的问题。2017年,仇成伟团队设计了短波长入射下焦斑沿光轴方向稳定保持亚波长特性达12λ的光针分布的平面超振荡透镜,并结合共聚焦成像原理,搭建了基于405 nm振幅型平面超振荡透镜的远场超分辨显微成像系统[40]。通过样品扫描的方式,在空气中获得纯光学65 nm的分辨率远场超分辨成像效果。同时,由于设计的焦点介于超振荡标准与超临界标准之间,使得透镜具有低旁瓣的优势,具有较高的信噪比,如图21所示。 图21 利用平面超振荡透镜对变高度物体三维成像结果。(a)由矩形孔阵列形成的三维渔网结构草图;(b)渔网结构的扫描电镜图;(c~e)通过透射模式显微镜,激光扫描共聚焦显微镜及超振荡显微镜分别对三维渔网结构的成像效果图[40] Fig.21 Three-dimentional imaging of the varying height object through planar SOLs. (a)Sketch of a 3D fishnet wedge composed of etched array of rectangular holes; (b)top-view (x-y plane) SEM image of the fishnet wedge. (c~e)the imaging results of this wedge by transmission mode microscopy(T-mode), laser scanning confocal microscopy (LSCM), and SCL microscopy[40] 图22 平面超振荡透镜高密度数据存储。(a)利用超振荡透镜光针实现热辅助磁记录的工作原理;二元光针超振荡透镜分别在(b)空气,(c)SiO2,(d)GaP介质中的径向透过率分布[97];(e)身份识别系统概念说明图[98] Fig.22 High density data storage based on SOLs. (a)Working principle of heat assisted magnetic recording(HAMR) realized by optical needle SOL, the radial transmittance distribution of the binary optical needle SOL mask design for air, SiO2 and GaP is given in (b), (c) and (d) respectively[97]. The transparent areas are white while the opaque areas are black; (e)illustration for identity verification[98] 在超高密度数据存储方面,2014年,新加坡南洋理工大学和英国南安普顿大学共同提出一种基于超振荡透镜的热辅助磁性写入技术[97],如图22(a)~22(d)所示。为了降低旁瓣,该超振荡聚焦透镜采用了超振荡光针设计的办法。该透镜的等效数值孔径达到了4.17,对波长为473 nm的圆偏振光进行聚焦。2017年,新加坡国立大学仇成伟团队又提出一种通过在三维空间形成超分辨焦点的方式实现光诱导磁全息的办法[98],如图22(e)所示,拟通过这种方法提高单位体积内数据的存储量。2018年,该课题组又提出将平面超振荡透镜用于高分辨振动成像[99],借助反斯托克斯拉曼散射显微镜对生物样品进行成像,分别在轴向及径向获得了较高的分辨率,如图23所示(彩图见期刊电子版)。 图23 基于超振荡透镜的反斯托克斯成像。(a)用于振动成像的超临界聚焦相干反斯托克斯拉曼散射显微平台示意图;(b)牙齿在XY平面上的相干反斯托克斯图像[99] Fig.23 Anti-stokes imaging based on SOLs. (a)Schematic diagram of the supercritical focusing coherent anti-Stokes Raman scattering(SCF-CARS) microscopy platform for vibrational imaging; (b)CARS image of the tooth in x-y plane[99] 本课题组研究发现,无论将平面超振荡透镜应用于超分辨远场非标记显微成像还是高密度数据存储领域,都是借助其高度可控的远场光场定制能力实现的。未来,可将超振荡透镜光场定制与实际应用需求相结合,对平面超振荡透镜阵列中的透镜单元进行光场差异化定制。 综上所述,目前国内外学者对平面超振荡透镜进行了广泛而深入的研究,并取得了一些突破性成果,但还有很多问题未能解决。平面超振荡透镜的焦点尺寸经历了最初定义的超振荡标准(0.38λ/NA)到为了减小旁瓣、增大焦深的超临界标准(焦点尺寸介于0.38λ/NA与瑞利衍射标准之间)的变化。为了将平面超振荡透镜更好地向实际应用方面推广,科学家们也做出了各种努力。在平面超振荡透镜的优化设计方面,现有的平面超振荡透镜主要基于最优化设计方法对目标进行约束优化,从而获得需要的光场分布,这使得实际优化过程中存在迭代计算效率低、结果发散且难以对平面超振荡透镜后表面光场进行灵活控制等问题。在超振荡透镜的聚焦效率方面,现有的平面超振荡透镜主要为二元振幅型、二元相位型以及二元振幅相位型3种,其中二元振幅型的聚焦效率最高仅为16%,降低了其在超分辨远场显微成像中的目标图像强度。二元相位型平面超振荡透镜通过在透明介质材料上刻蚀一些环带,有效提高了这类透镜的聚焦效率,然而经验表明,二元相位型平面超振荡透镜的聚焦效率最高也仅为40%。因此,为了更大程度地提高这类透镜对光的能量集中率,需要研制更高效率的平面超振荡透镜。在平面超振荡透镜制备方面,最早是基于亚波长特征尺寸的环带,利用聚焦离子束或电子束曝光等技术进行加工的,这类加工工艺存在成本高、耗时长、无法制作大尺寸平面超振荡透镜的问题。接着,研究人员又将平面超振荡透镜的特征尺寸提高到了非亚波长量级,分别用深紫外加工设备和激光直写设备对数百微米的平面超振荡透镜进行了加工,然而这类制备工艺在对大尺寸结构进行定义时需要采用拼接的办法,对准精度较低,给大尺寸乃至圆片级平面超振荡透镜的研制带来了挑战。在平面超振荡透镜的应用方面,以超分辨远场非标记显微成像、高密度数据存储这两类应用为代表。受超振荡透镜成像原理的限制,在超分辨远场非标记显微成像领域的研究中,都是结合共聚焦显微成像系统,通过扫描拼接对特定物体进行成像的,这需要对现有的共聚焦成像系统进行改装才能完成,另外实验对现有工作条件要求较高且成像需要扫描过程才能完成,因此后续需要对平面超振荡透镜的新的可能应用场景进行挖掘。 平面超振荡透镜因其在集成化、批量化制备方面以及远场超分辨聚焦方面具有明显优势,受到平面衍射光学及微纳光学领域研究人员的广泛关注。当前平面超振荡透镜面临从优化设计到实际应用转变的关键转折点,从性能提升到应用场景上仍存在改进空间。 现有平面超振荡透镜无论是二元振幅型还是二元相位型都是基于二元衍射结构进行优化设计的,已报到的平面超振荡透镜的聚焦效率最高也仅为40.6%。因此,提高平面超振荡透镜的聚焦效率具有十分重要的意义。通过增加现有透镜的相位水平可提高透镜的聚焦效率,与光学超表面结构[100-103]类似,将二元相位型平面超振荡透镜设计成多相位水平甚至是连续相位水平也可显著提高透镜的聚焦效率。另一方面,从材料的性质入手,研制基于二维材料的高效率平面超振荡透镜也是一种可能的解决方案。 与传统透镜类似,平面超振荡透镜也面临色散问题,利用平面超振荡透镜光场可任意定制这一特性,开发宽波段消色差平面超振荡透镜以及色散定制的分光元件都是可行的。通过多层结构优化设计或改进多目标优化算法为连续宽波段聚焦提供了可能性。另一方面,基于平面超振荡透镜研制的色散可定制的分光元件在微型光谱成像仪、便携式生物成像光谱仪等领域具有应用前景。 现有的平面超振荡透镜的应用主要集中于远场超分辨非标记显微成像、高密度数据存储等领域,而这两种应用场景对硬件实验条件有一定的要求,且发展已较为成熟。通过改进平面超振荡透镜的视场以及聚焦效率,将平面超振荡透镜阵列用于提供超分辨点阵,从而实现大视场超分辨成像也是一种可能的应用场景。此外,利用超振荡透镜优越的光场可控性,可以实现不同阵列单元中光场的差异化定制,从而对特定样本进行成像。 本文主要从实际应用角度出发概述了平面超振荡透镜在实际应用方面需要考虑的如焦深、视场、聚焦效率、工作波长等性能参数的演变过程,并在该过程中对本课题组在相关方面所做的研究进行了讨论,在此基础上对平面超振荡透镜实际应用性能需要改进之处提出了解决思路。接着,探讨了平面超振荡透镜的优化设计方法及制备工艺进展,总结了目前存在的问题以及发展趋势。最后,对平面超振荡透镜目前的应用情况进行了分类归纳,在此基础上提出了未来的可能发展方向。 纵观超振荡透镜从概念提出到走向实际应用的发展历程,每一次性能参数的升级优化都是便于其更好地服务于实际应用而进行的。放眼未来,平面超振荡透镜将在光场可控定制、低成本批量化制备、芯片级显微成像系统几大方面得到更为密切的关注。而且注意到,由于平面超振荡透镜独特的成像机制,如何更好地发挥其在超分辨成像系统中的作用值得更深入的思考,与此同时,需要考虑平面超振荡透镜的像差消除问题。2.2 超振荡透镜的焦深及轴向光场控制
2.3 超振荡透镜的视场及径向光场控制
2.4 平面超振荡透镜的聚焦效率
2.5 超振荡透镜工作谱段及带宽
3 平面超振荡透镜的优化设计方法
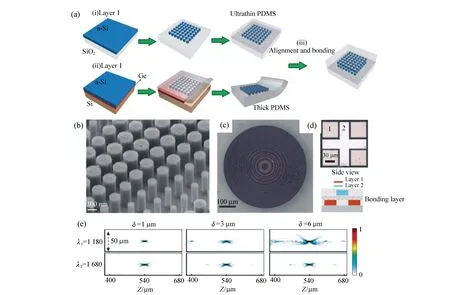
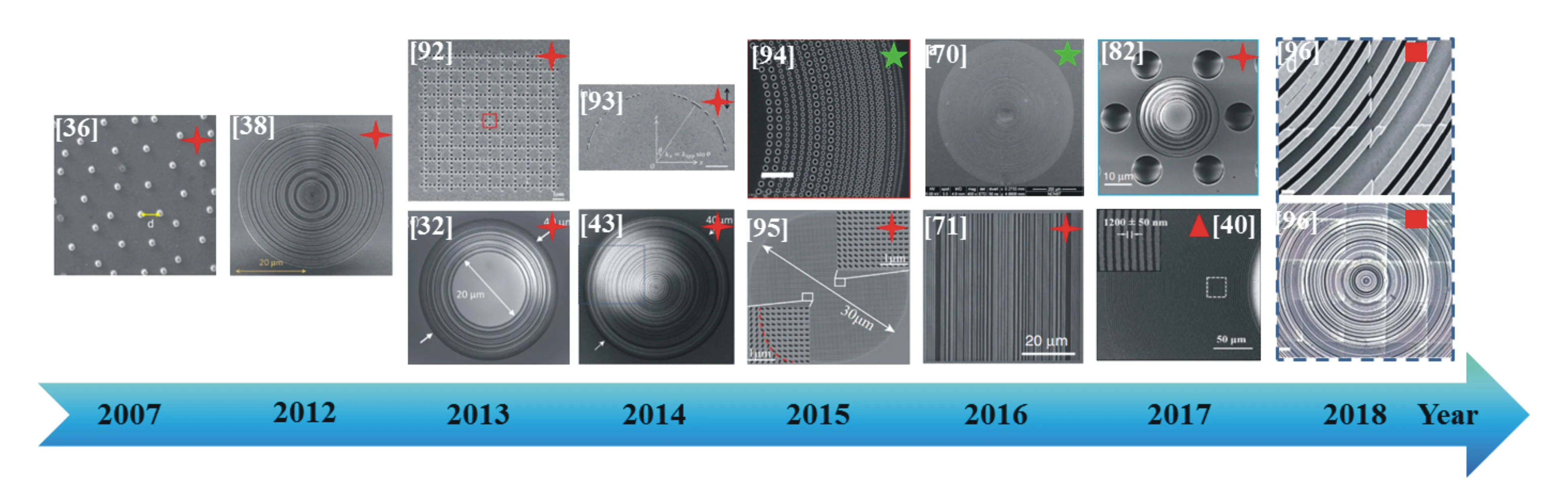
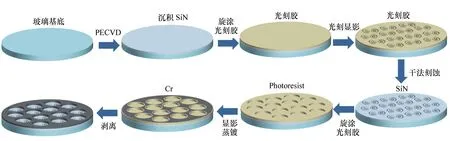
4 平面超振荡透镜的制备工艺进展

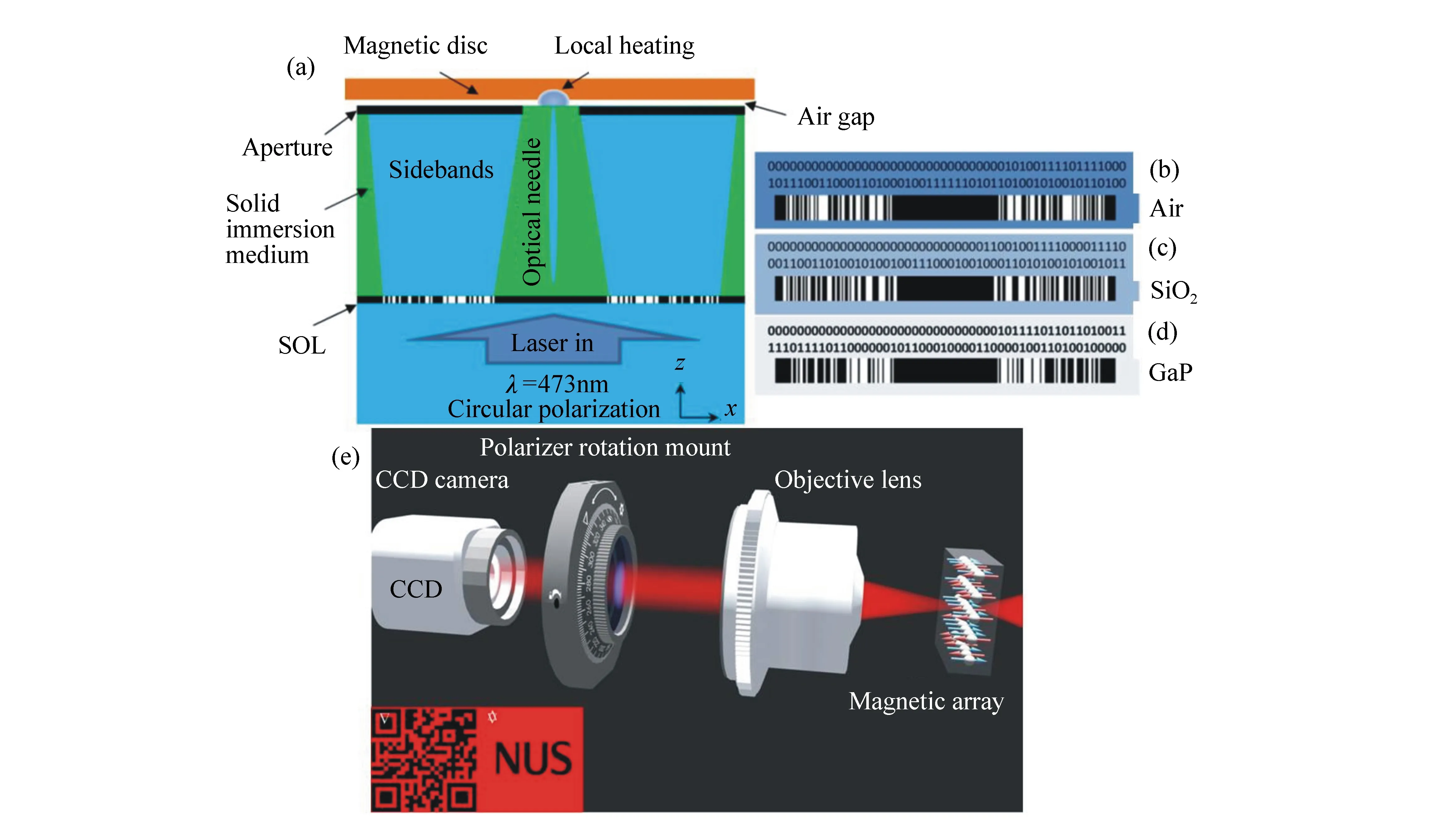
5 平面超振荡透镜的应用研究进展

6 未来发展方向展望
6.1 高聚焦效率的平面超振荡透镜
6.2 色散可调制的平面超振荡透镜
6.3 平面超振荡透镜用于芯片级显微成像系统
7 结束语

