广义拓扑中的K-半层空间和函数插入

胡星宇，李东行

1.广州工商学院 基础教学部，广东 广州 510850； 2.广东金融学院 金融数学与统计学院，广东 广州 510521）

1 预备知识

下面介绍一些基本概念和符号：

定义1［2］设X 是一非空集合，如果X 的子集构成的集族μ 满足下面2 个条件，那么μ 称为X 上的广义拓扑， ),( μX 称为广义拓扑空间：

(2)μ 的任意多个元素的并属于 .μ

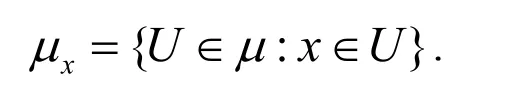
定义2［2］设是空间，X 被称作正则空间.如果对X 的任意2 个不相交的闭子集和都存在，使和,并且

定义3［3］设是广义拓扑空间，ℝ 是赋予通常拓扑的实直线.是广义上半连续函数（广义下半连续函数)，若对每一，集合是开集.

定义4［4］广义拓扑空间被称作是紧空间，如果X 每一个开覆盖都具有一个有限子覆盖.

定义5［3］设是广义拓扑空间，是赋予通常拓扑的实直线.是广义下(上)半连续函数，如果对于X 的每一个紧子集K ， f 在K 上有最小（最大）值.

定义6［1］空间X 被称作半层空间，如果存在映射满足：

定义7［1］设X 是空间，则下列等价：

定义8［3］对于广义拓扑空间X，将X 上的全体下（上）半连续函数构成的集合记作.

2 主要结果

(1)空间X 是半层空间；

可以验证U 满足（2）中的性质（i）-（iii），因为符合定义2.1 的（1）和（2），可以很容易验证U 满足（2）中性质（i）和（iii）.

（2）⇒（1）.

证明：