三阶微分方程组特解的按列比较法
2020-01-08 03:28吴幼明林晓莹
惠州学院学报 2019年6期
吴幼明,林晓莹
( 佛山科学技术学院 数学与大数据学院, 广东 佛山 528000 )
求微分方程组的特解[1-8]是微分方程理论的重要内容之一,很多学者都已经研究得到大量有用的研究成果.文献[5-7] 分别给出了方程组和在的形式时的特解公式,文献[8]虽然给出了一个三阶方程 0=-′ BffA 的通解,但未对特解进行讨论.文章在文献[5-8]的基础上,采用按列比较法,给出了微分方程组当的形式时的特解公式,这是文献[5-7]的推广,亦是文献[8]的补充,因此更具有普遍性.
1 符号
给出矩阵微分方程
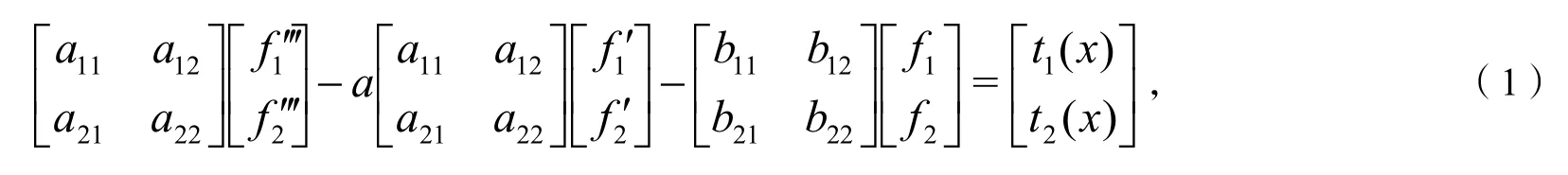
因此,方程(1)整理后为:

2 非齐次方程组的特解
对于矩阵微分方程(2),设

其中, ki, li, mi, ni, γi(i =1,2)是常数.
根据待定矩阵法,可设方程组(2)的1 个特解为:
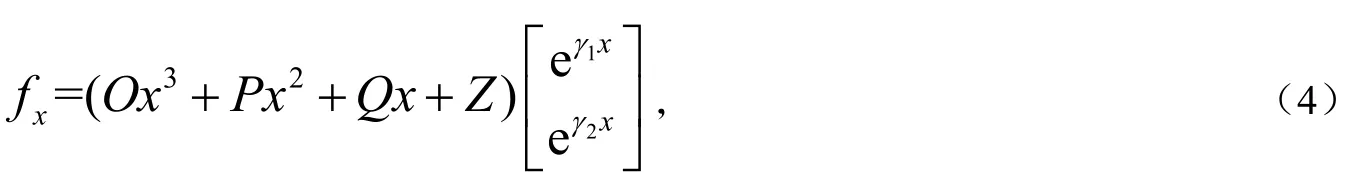
将式(4)代入矩阵微分方程(2)中,整理并比较x 的同次幂系数和指数函数的系数得:

由式(5)取第i )2,1( =i 列得:
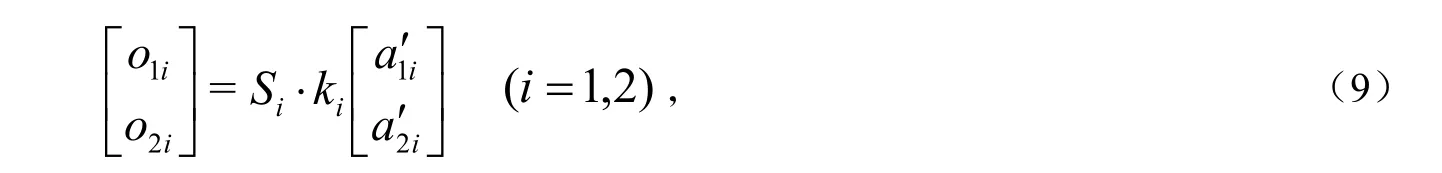
有

由式(6)取第i )2,1( =i 列得:

将式(9)代入式(11)中整理得:

由式(7)取第i )2,1( =i 列得:

将式(9)和式(11)代入式(13)中整理得:

由式(8)取第i )2,1( =i 列得:
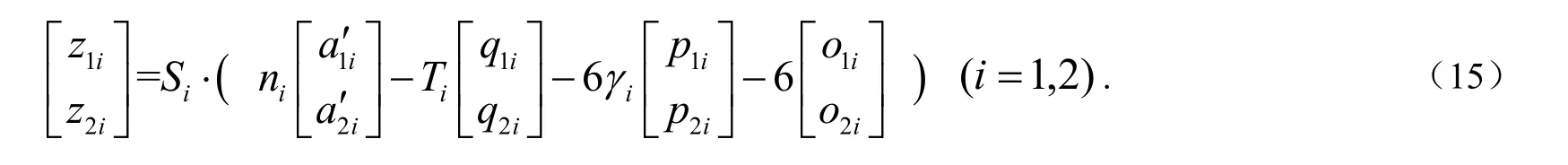
将式(9)、(11)、(13)代入式(15),可得:
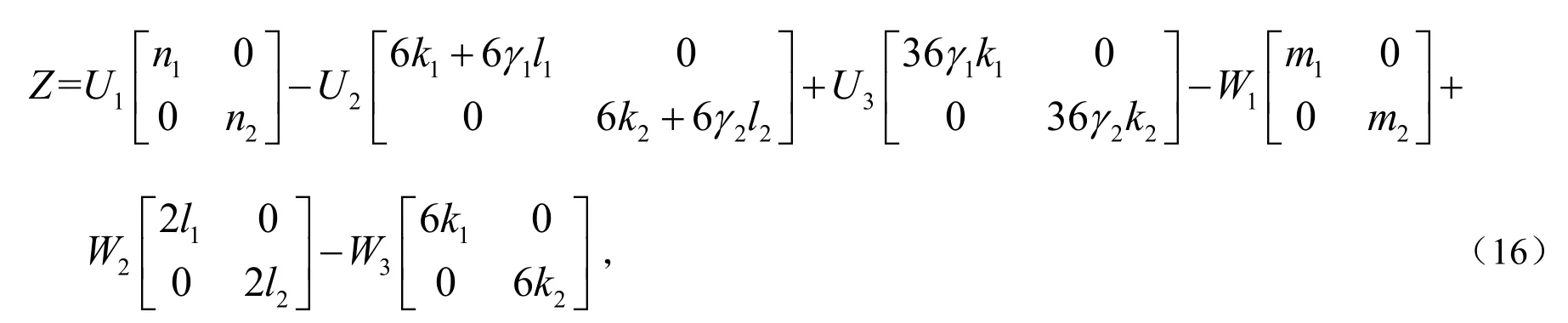
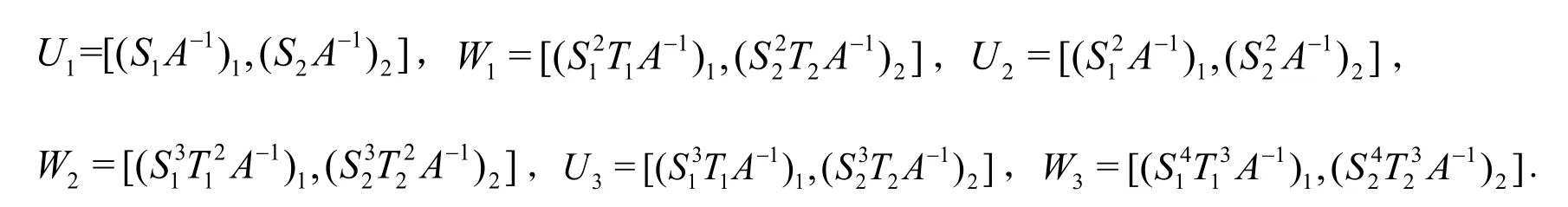
将所求得的O、P、Q、Z 的值代入式(4),得方程(1)的1个特解为:

3 算例
用本文方法解矩阵微分方程的特解:
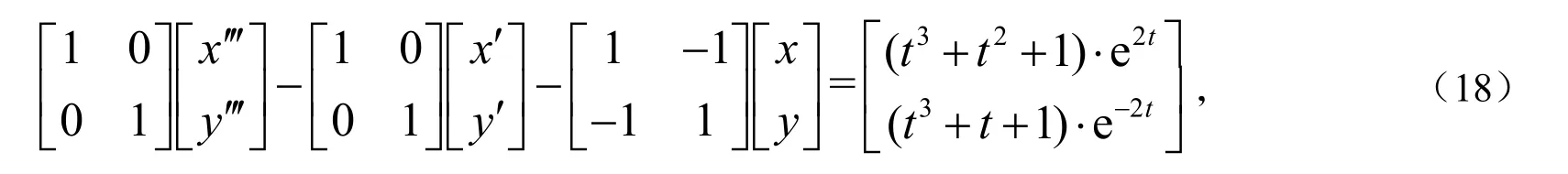
则:

则矩阵微分方程(18)的1 个特解为:

经检验,式(19)是矩阵微分方程(18)的1 个特解.
4 结语
文章在二阶微分方程组研究的基础上,根据按列比较法和待定矩阵法,进一步探讨得出了一类不含二阶导数项的三阶微分方程组的特解公式,并根据算例验证了公式的正确性.文章结果也可通过编写计算机程序进行计算.
猜你喜欢
哈尔滨商业大学学报(自然科学版)(2022年4期)2022-08-18
数学物理学报(2022年2期)2022-04-26
邵阳学院学报(自然科学版)(2021年4期)2021-09-14
吉林大学学报(理学版)(2020年3期)2020-05-29
苏州科技大学学报(工程技术版)(2019年4期)2020-01-04
三峡大学学报(自然科学版)(2019年5期)2019-10-17
电子技术与软件工程(2018年10期)2018-07-16
速读·中旬(2018年4期)2018-04-28
北京航空航天大学学报(2017年4期)2017-11-23
中学生数理化·七年级数学人教版(2017年2期)2017-03-25

