非线性中立型多变时滞积分微分方程的稳定性
2020-01-08 03:28:52黄明辉
惠州学院学报 2019年6期
黄明辉,刘 君
(广州城建职业学院 数学教研室,广东 广州 510925 )
1 预备知识
非线性微分方程周期解的存在性、唯一性、正解性和稳定性等问题的研究,Lyapunov 方法是最常用的方法[1-2].Ardjouni[3-4]、Jin[6-7]等学者利用不动点定理研究了微分方程的稳定性,并取得了一系列的研究成果[3-10].文献[4]利用Banach 不动点定理,研究了线性中立型多变时滞积分微分方程

受此启发,本文考虑以下非线性中立型多变时滞积分微分方程零解的渐近稳定性


2 主要结果
引理1 方程(2)等价于

对方程(2)给出下列假设:
(H1),且可微,当,其中,.
(H2)是全局Lipschitz 连续函数,即存在正数,

(H3)存在连续函数和常数,对,

定理1 设(H1)-(H3)成立.若,则方程(2)的零解渐近稳定.
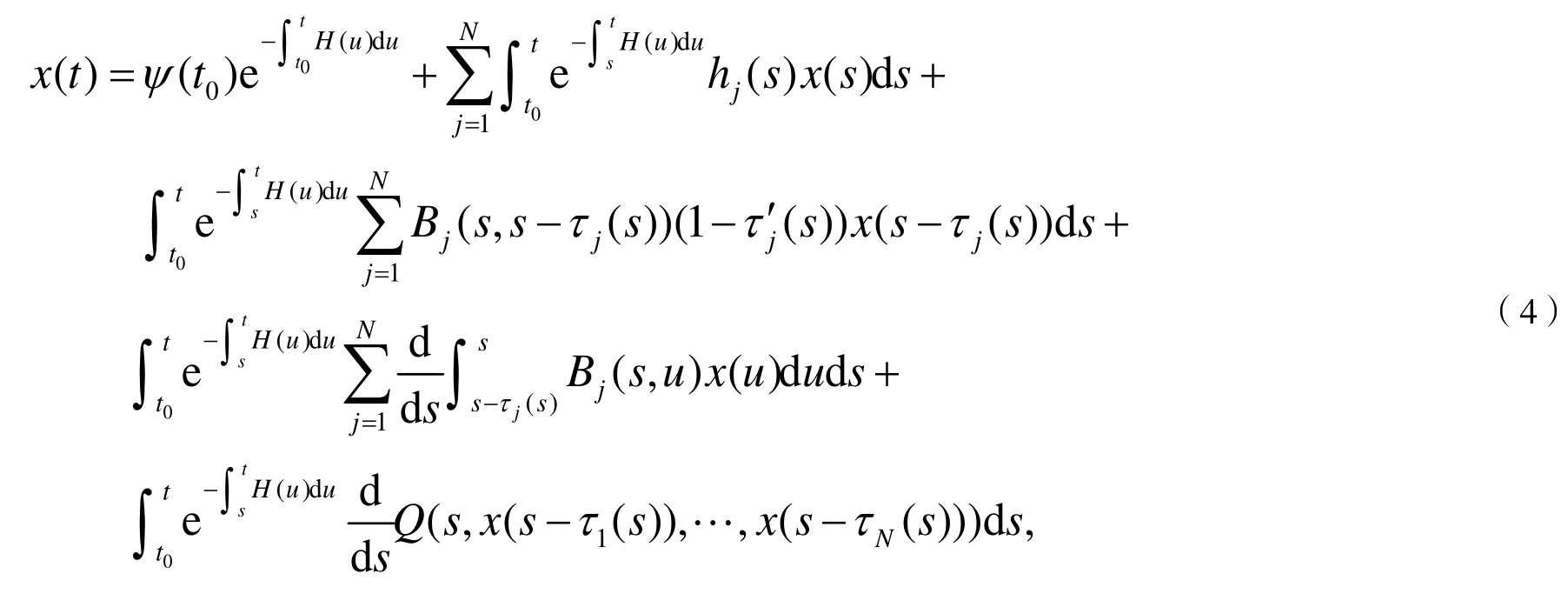
通过分部积分并整理,得





由(H3)知,.因此,当t →∞时,.同样地,可以证明当t →∞时,式(6)中其他项也趋向于零.因此,当t →∞时,,故.

由条件(H3)可得,P 是一个压缩系数为α 的压缩映射.所以,由压缩映射原理得,P 在空间Sψ上存在唯一不动点,它是方程(2)的解.且满足当,当t →∞时,.
为了证明渐近稳定性,需要证明方程(2)的零解是稳定的.假设给定任意和满足.如果是方程(2)的一个解,其中,对任意,.下面证明.

3 实例
例1 考虑以下非线性中立型多变时滞积分微分方程


4 结论
文章利用不动点理论,研究非线性中立型多变时滞积分微分方程零解的渐近稳定性.所研究的方程引入了,比文献[4]的方程更加一般化.并且文献[4]的定理要求时滞τ 二次可微,,但定理1 中仅要求τ 连续可微,进一步削弱了对时滞τ 的要求,从而推广了文献[4]的相应结果.
猜你喜欢
山东师范大学学报(自然科学版)(2021年2期)2021-07-20 05:25:18
数学物理学报(2020年5期)2020-11-26 06:06:48
数学物理学报(2020年4期)2020-09-07 09:14:16
陕西理工大学学报(自然科学版)(2019年4期)2019-08-30 02:33:16
中等数学(2019年12期)2019-05-21 03:22:16
潍坊学院学报(2015年6期)2015-12-01 12:58:35
河北科技大学学报(2015年6期)2015-03-11 16:16:46
四川师范大学学报(自然科学版)(2015年2期)2015-02-28 14:07:40
应用数学与计算数学学报(2014年3期)2014-09-26 12:03:52
河北大学学报(自然科学版)(2014年4期)2014-07-24 05:51:48

