时变时滞奇异摄动不确定控制系统的状态反馈控制器设计
2020-01-08 03:29陈爽
惠州学院学报 2019年6期
陈 爽
(吉林师范大学 数学学院,吉林 长春 130000)
时滞的存在往往导致控制系统的不稳定和性能指标的退化.时滞系统研究的热点问题主要有:时滞依赖稳定性分析、镇定控制器设计、性能设计以及滤波问题等.研究的核心问题主要围绕如何减小所得结果的保守性[1-2].因此,无论是为了理论体系的完善和发展,还是为了使理论能早日应用于实际,对具有广义时滞系统在研究内容和研究方法上,都亟待创新、发展和系统化[3 -11].
1 问题描述
考虑如下时变时滞奇异摄动不确定控制系统(S )[1 4]:



对系统(S ),设计状态反馈控制律:

将此控制律代入原系统(S ),构成一个闭环系统(S*):
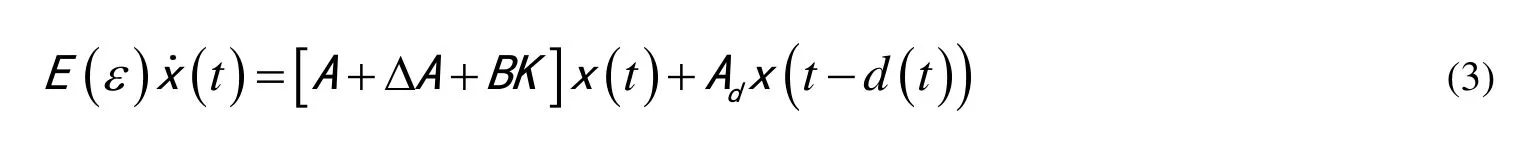
引理 1[3]给定,对矩阵 S1、 S2和 S3,如果:
引理 2[3]如果存在对称矩阵且满足以下LMI 条件:
引理 3[4]给定适当维数的矩阵Y 、D 和E ,其中Y 是对称矩阵,不确定性函数,所以


2 主要内容

则系统(S*)渐近稳定,并且是系统(S*)的输出反馈控制律,其中.
证明 定义如下Lyapunov 泛函

其中,Q 是对称正定矩阵.
由于

可知

故
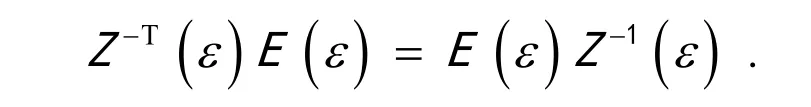
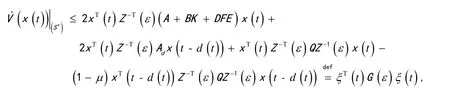
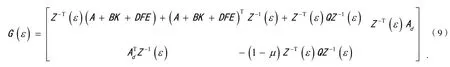

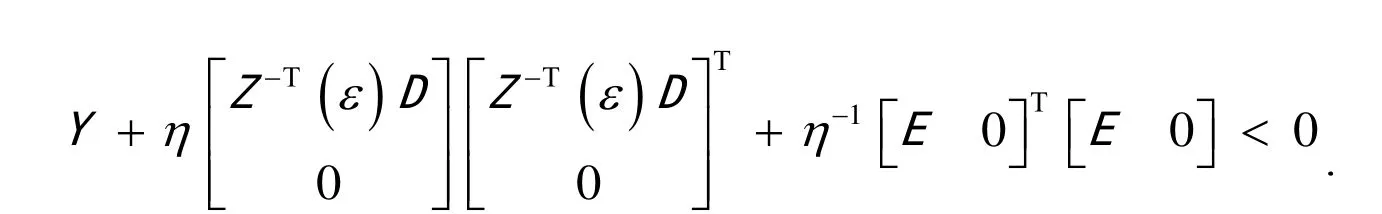
由Schur 补引理,得

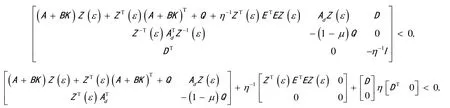
即

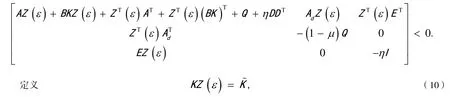
得到
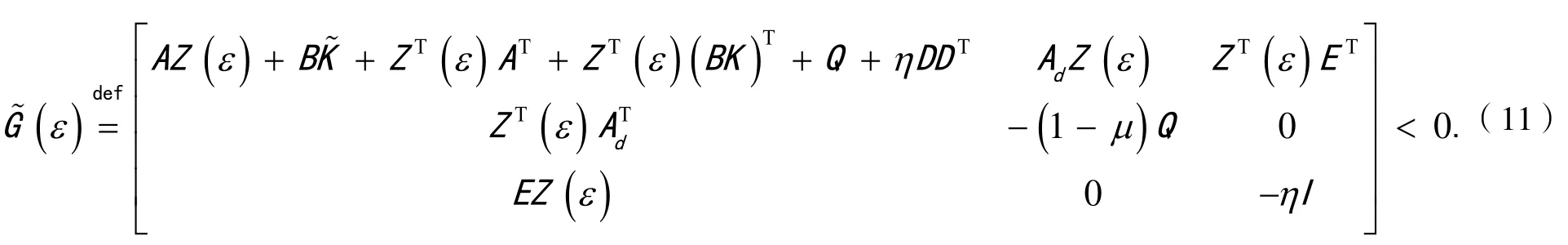

3 结语
该文讨论了一类状态中含有时滞的奇异摄动不确定系统的状态反馈控制问题,结合LMI 和Lyapunov 方法给出了一种新的方法,最终得到了保证闭环系统渐进稳定的充分条件及相应的输出反馈控制律.
猜你喜欢
中国交通信息化(2020年4期)2021-01-14
数学物理学报(2020年5期)2020-11-26
自动化学报(2019年12期)2020-01-19
中国特种设备安全(2019年9期)2019-12-03
中国惯性技术学报(2019年3期)2019-10-15
自动化学报(2019年6期)2019-07-23
北方工业大学学报(2019年5期)2019-03-30
智富时代(2017年4期)2017-04-27
智富时代(2017年4期)2017-04-27
中国铁道科学(2015年4期)2015-06-21

