基于子阵的频控阵自适应波束形成算法*

张 晶，谢军伟，王 博，孙渤森

（1.陕西交通职业技术学院，西安 710018；2.空军工程大学防空反导学院，西安 710051；3.西安财经学院，西安 710100）

0 引言

当前，基于数字波束形成技术的频控阵（Frequency Diverse Array，FDA）干扰对抗技术研究还比较少。文献［1-2］中研究了基于对称频移分布和sin函数分布的矩形波束形成技术，在特定的距离、角度二维空域形成主瓣波束，能够减轻矩形区域外雷达受干扰程度，同时降低被截获概率。文献［3］基于低截获波束设计准则，给出了几种FDA 低截获波束设计方案。文献［4-5］将传统波束形成算法应用于频控阵，实现了距离维的干扰抑制，但没有对主瓣畸变及干扰位置变化时输出性能的改变进行分析。针对文献中对于目标与干扰距离维可分、角度维接近情况下的抑制方法研究较少的情况，本文在文献［6］中FDA-BFF、FDA-MIMO 及BFF-MIMO 三种接收机结构的基础上，提出了基于双边小方差无畸变响应（Two-Side Minimum Variance Distortionless Response，TS-MVDR）的子阵FDA 波束形成算法。

1 基于MVDR 的FDA 波束形成

1.1 MVDR 算法模型

波束形成的实质是通过对各阵元加权进行空域滤波达到增强期望信号、抑制干扰的目的。波束形成器一般基于某种准则设计以确定自适应权，常用的波束形成器准则有最小方差无失真响应（Minimum Variance Distortionless Response，MVDR）准则、最小均方误差、最大信噪比准则等。在理想情况下，这4 种准则得到的权是等价的，其中MVDR 准则算法原理简单，能够在干扰区形成有效零限，应用较为广泛［7］。

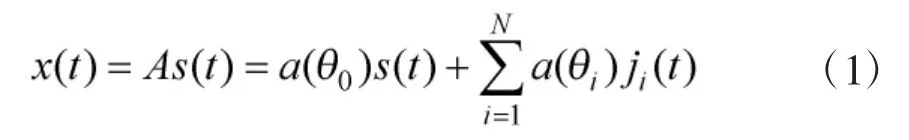
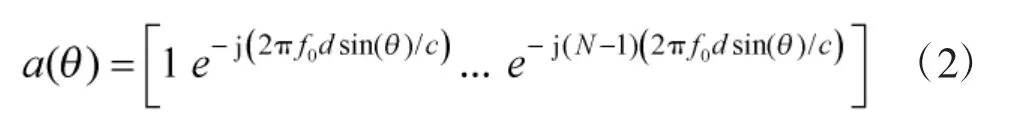
阵列输出可表示为：

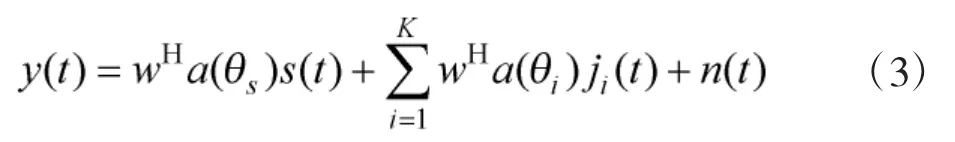
其中，wH表示接收端加权矢量，n（t）表示接收机噪声矢量。MVDR 波束形成准则用公式可表述为：

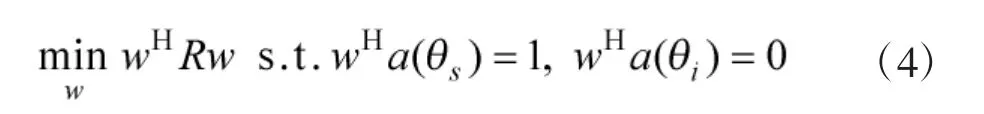
求解式（4），得对应的加权矢量的解析表达式为：

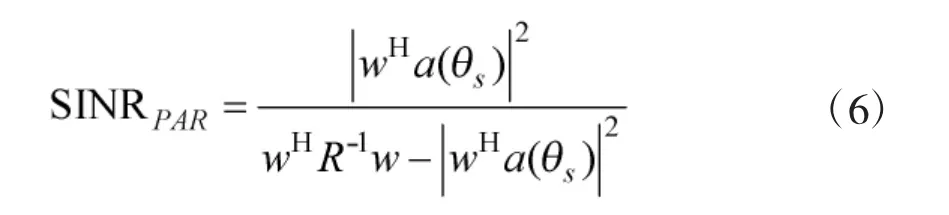
1.2 一维MVDR 算法应用

一维MVDR 算法，就是直接将各结构导向矢量带入式（5），求解最优加权矢量。对FDA-BFF 结构，阵列输出为：

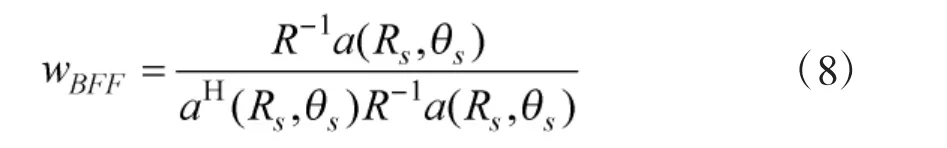
输出信干噪比可为：

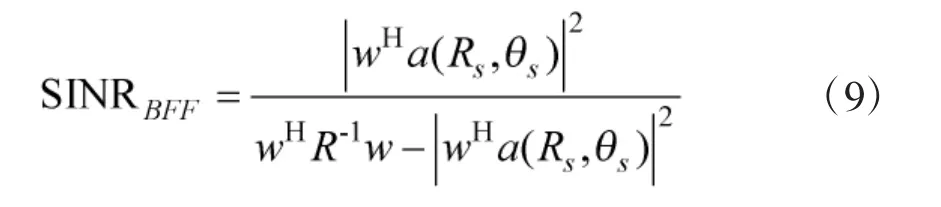
对FDA-MIMO 结构，阵列输出可表示为：

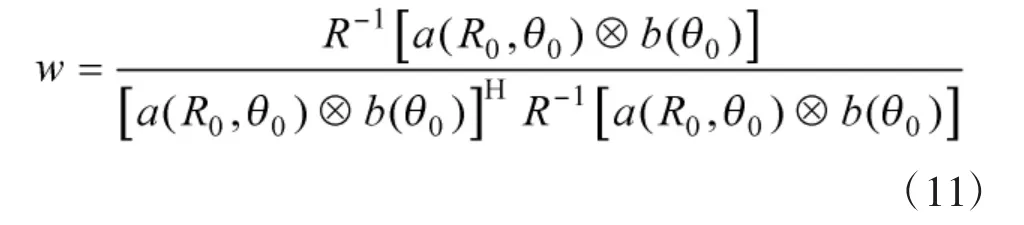
设FDA-BFF 阵元数为30，频差Δf=10 KHz，目标位于（30 km，30°），干扰位于（32 km，31°），相控阵、FDA-BFF 接收结构的方向图如图1、图2 所示。改变干扰位置，设干扰位于（32 km，42°）处，利用MVDR 进行波束形成，得FDA-BFF 波束如图3 所示。

图1 N=9 时相控阵天线方向图

图2 N=9 时FDA-BFF 天线方向图

图3 N=9 时FDA-BFF 天线方向图

由图1 可知，相控阵结构可以在干扰角度形成一条仅与角度相关而与距离无关的“零限带”，但当干扰与目标角度接近时，会产生主瓣畸变等问题。由于阵元间频差的引入，图2 中的FDA-BFF 结构产生距离角度二维相关的波束，可在（32 km，31°）干扰位置处形成零限的同时，在目标位置形成保持增益。由图3可知，当干扰的空间位置满足FDA-BFF 结构波束的距离-角度耦合关系时，即干扰位于FDA-BFF 的空域主瓣内时，FDA-BFF 形成的主瓣在目标位置处依然发生了畸变，波束形成器输出性能下降。

对于FDA-MIMO 结构，设频差Δf=10 KHz，目标位于（30 km，30°），干扰位于（32 km，31°），当阵元数分别为9、30 时，求解MVDR 权矢量，得到对应的方向图及干扰、目标距离处的角度维方向图如图4、5 所示。由图看出，当N=9 时，通过应用一维MVDR能够得到在目标处增益最大，在干扰处增益置零的方向图；但当N=30 时，方向图出现较大程度畸变，无法找到相应的主瓣区域，但在干扰位置处仍能形成零限。

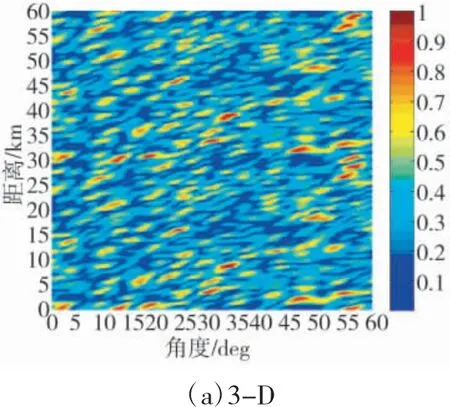
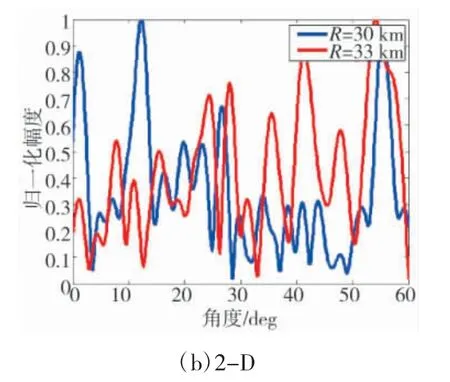
图5 N=9 时一维MVDR 求取的FDA-MIMO 方向图

1.3 双边MVDR 算法在FDA-MIMO 中的应用

为解决式（5）在MIMO 中直接应用算法复杂度过高的问题，充分利用MIMO 导向矢量中的克罗内克结构，采用TS-MVDR［8］进行最优权矢量求解，即将MIMO 波束形成过程虚拟为发射波束形成和接收波束形成两个过程，两过程中的导向矢量分别为a（R，θ）和b（θ），利用式（4）分别求取对应过程的最优权矢量，再求取两最优权矢量的克罗内克积作为最终的权重矢量，该过程可描述为：

假设FDA-MIMO 拥有M 个阵元，MVDR 需通过式（11）求解M2个系数向量；而双边MVDR 相当对单一子阵、子列分别进行MVDR 波束形成，最后通过克罗内克积综合为一个权矢量，仅需求解2 M个系数向量，大大降低了计算量。图6 仿真了干扰位于（32 km，31°）时阵列的输出方向图。

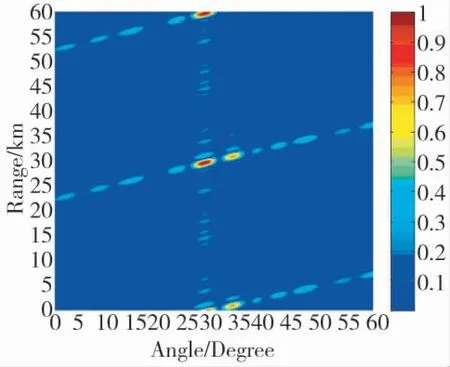
图6 N=31 时TS-MVDR 求取的FDA-MIMO 方向图

由图6 可看出，利用TS-MVDR 算法进行波束形成，在阵元数较大的情况下方向图不会出现严重的畸变；但当干扰与目标角度相近时，仍会产生主瓣畸变。这是因为TS-MVDR 本质上是对算法计算量的优化，当干扰与目标角度相近时，在对单一子阵、子列分别进行MVDR 波束形成的过程中已经存在主瓣畸变的问题，求取克罗内克积的过程对主瓣畸变问题没有优化作用。

2 基于子阵的sin-FDA 结构

2.1 非线性频偏引入

文献［9］指出频控阵发射波束会出现距离和方位角响应的耦合问题，因而无法利用其无模糊的实现目标距离和方位的二维联合估计。上述分析中，当干扰位置符合FDA-BFF 结构波束图的距离-角度耦合关系时，会产生主瓣峰值畸变。将一维均匀线性频控阵（Uniform Linear Array Frequency Diverse Array，ULA-FDA）划分为在中心对称的两个子阵，再在阵元间引入不同的非线性频偏增量，得到基于子阵的sin-FDA 结构。

2.2 中心对称子阵结构

中心对称子阵结构是将基本的ULA-FDA 阵列划分为两个关于参考阵元中心对称的子阵，阵列结构如图7 所示［15-17］：

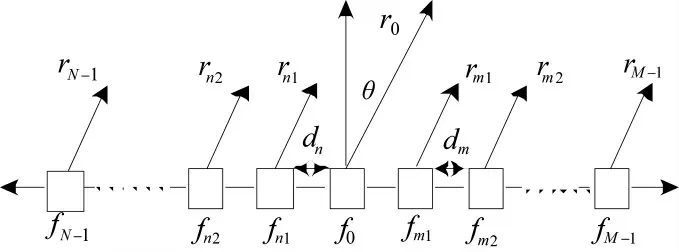
图7 中心对称FDA 子阵结构

子阵1 的阵元个数为n，阵元间的频偏为Δf1，子阵2 的阵元个数为m，阵元间的频偏为Δf2，则子阵1 第n 阵元和子阵2 第m 阵元的载频可表示为：

窄带条件下，子阵1、2 各阵元发射信号可表示为：

给定一个远场目标点（R，θ），子阵1 第n 阵元和子阵2 第m 阵元的发射信号到达目标点的信号形式为：

整个阵列在远场位置的场强为子阵1 和子阵2在远场处形成场强的叠加。图8 为以中心对称子阵结构为接收阵列所得的天线方向图，方向图中的波束主瓣在扫描位置处形成了点状波束。

图8 中心对称子阵log-sin-FDA 天线方向图

3 仿真结果

仿真1：TS-MVDR 算法的应用。

首先分析当干扰与目标位置在角度及距离上都比较接近时，TS-MVDR 算法在基于子阵结构的sin-FDA-BFF 及sin-FDA-MIMO 结构中的应用性能。设中心对称结构中两子阵的阵元数都为15，子阵阵元间的频差Δf 都为Δf=10 KHz，目标位于（30 km，30°），干扰位于（32km，31°），得到图9～图12。从图中可知，与采用线性频偏的阵列结构在目标位置处所形成的“倾斜”波束不同，基于子阵的sin-FDA-BFF 结构以及sin-FDA-MIMO 结构在目标位置处都能形成点状波束。同时，干扰位于（32 km，31°）、（32 km，42°）时都可以在保持目标点增益的同时对干扰进行有效抑制。

图9 子阵sin-FDA-BFF 天线方向图（3-D）

图10 子阵sin-FDA-BFF 天线方向图（2-D）

图11 子阵sin-FDA-MIMO 天线方向图（3-D）

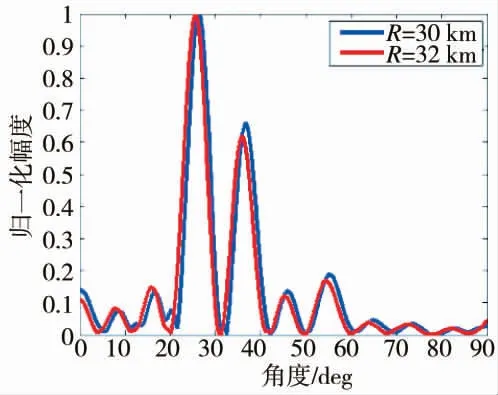
图12 子阵sin-FDA-MIMO 天线方向图（2-D）

图13 子阵sin-FDA-BFF 天线方向图（3-D）

图14 子阵sin-FDA-BFF 天线方向图（2-D）

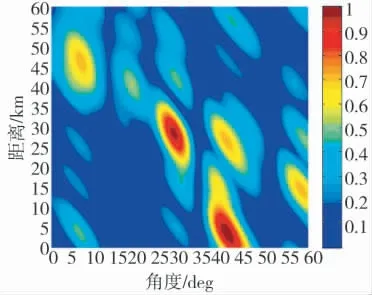
图15 子阵sin-FDA-MIMO 天线方向图（3-D）

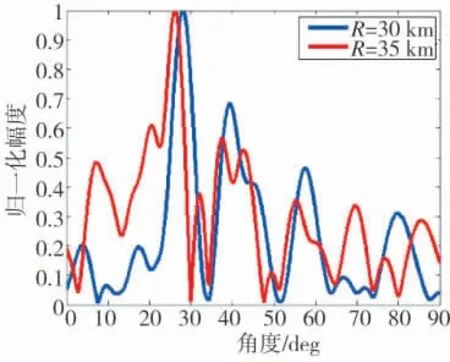
图16 子阵sin-FDA-MIMO 天线方向图（2-D）

改变干扰位置为（35 km，30°），其余仿真参数不变，得到图13～图16。当干扰与目标距离维接近同时角度维不可分时，传统的相控阵波束由于仅仅具有角度维的分辨力而没有距离相关性，因而相控阵方向图中的“零陷带”会对主瓣方向的增益产生影响，基于线性频偏均匀线阵结构的FDA-BFF 及FDA-MIMO 结构的方向图也会出现主瓣畸变。从图中可知，两种结构的方向图都得到了较为理想的效果。

仿真2：各类结构的输出性能对比。

首先对方向图进行比较，目标位置（30km，30°），干扰位置（35 km，30°），PRA 及FDA-BFF 结构中阵元数N=30，子阵sin-FDA-BFF、子阵sin-FDA-MIMO 结构中两子阵阵元数为15，分别采用三角函数及对数形式的非线性频偏增量，阵元间频差固定为Δf=10 KHz，利用MVDR 算法求取4 种结构的最优权矢量，在目标、干扰距离处各结构的角度维方向图如图17、图18 所示（为方便比较主瓣偏移情况和干扰的零限深度，目标距离处采用幅度图，干扰距离处采用dB 图）。

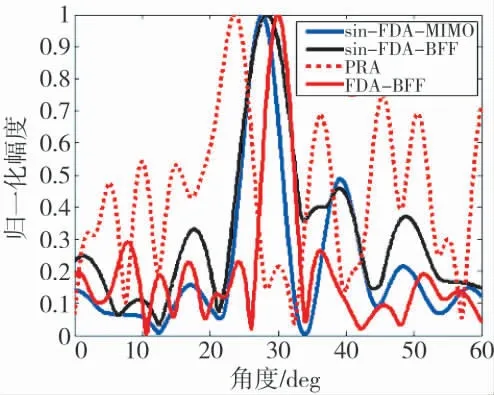
图17 各结构的角度维方向图（R=30 km）

图18 各结构的角度维方向图（R=35 km）

由图可知，当干扰与目标处在同一角度时，在目标距离处，PAR 的主瓣产生明显的畸变，而sin-FDA-MIMO、sin-FDA-BFF 及FDA-BFF 在目标处保持了较高增益。sin-FDA-MIMO、sin-FDA-BFF在目标位置处形成了点状波束，但与FDA-BFF 相比，波束主瓣发生了一定程度的峰值偏移。在干扰距离上，FDA-BFF、sin-FDA-MIMO（TS）形成的干扰最深，PRA 在干扰位置未形成较深的零陷。双边MVDR 将整个波束形成过程虚拟成发射与接收波束形成两个过程，对干扰进行了两维抑制。

4 结论

本文提出了基于TS-MVDR 的子阵FDA 波束形成算法。该算法在将阵列划分为两个引入不同非线性频偏的中心对称子阵结构的基础上，采用双边MVDR 算法降低计算量，得到了基于子阵的sin-FDA 波束形成方法。仿真验证表明所提方法在目标位置处形成点状波束的同时，可以有效抑制角度维不可分的干扰。但TS-MVDR 算法存在性能“凹口”的问题，这需要通过对MVDR 波束形成器目标函数的优化进行进一步的研究。