舰炮一维弹道修正弹的射击诸元解算方法

李 元

（中国船舶重工集团公司江苏自动化研究所，江苏 连云港 222006）

0 引言

通过在炮弹引信上增加轴向阻力器、减旋阻力器等阻力修正机构实现炮弹发射后的弹道修正，是一种行之有效的常规炮弹提升精度手段。美国的弹道修正引信（CCF）、英国的欧洲修正引信（ECF）、法国的萨姆普拉斯（SPACIDO）、瑞典的TCM 弹道修正弹、美国的PGK 引信、南非的二维弹道修正引信等均如此。国内从1994 年开始展开对弹道修正引信方面的研究，目前一维弹道修正的研制已接近国外水平，二维弹道修正研制水平与国外还存在5 年～10 年的差距［1］。

对一维弹道修正，常见的引信修正方式是沿弹体轴对称分布的阻力环。这种修正引信可以使用地面/舰面跟踪雷达测量弹道，经地面/舰面解算将开环修正指令发送至弹上［2-4］，也可以使用卫导/惯导的弹载定位装置实时获取弹道信息，经弹载计算机解算后控制阻力环开环［5］。一维弹道修正弹在阻力环不张开时，其弹道特性与无控常规炮弹完全一致，阻力环张开后，弹丸飞行的阻力迅速变大，纵向射程变短，进而改变原有弹道落点。特别的，阻力环张开越早，纵向修正能力越大，张开越晚，纵向修正能力越小。

目前，对一维弹道修正弹的气动布局和修正能力［6］、射击误差分离和对岸校射［7-9］等多个方面均有不同程度的研究。但对一维弹道修正弹发射前的射击诸元解算，尤其是应用于海军水面舰艇平台时的射击诸元解算，尚没有成熟的方法。本文针对舰炮平台的一维弹道修正弹，对诸元解算需求、射击航行风影响、气象影响等多个方面展开分析，明确了传统无控弹诸元解算方法已经无法适用于一维弹道修正弹的诸元解算，并提出一种精确的舰炮一维弹道修正弹射击诸元解算方法。

1 一维弹道修正弹对射击诸元的解算需求

常规炮弹的射击诸元包含方位角和高低角。其解算需求非常明确，对确定的目标，一般有两组诸元，分别为平射诸元和曲射诸元，正常取平射诸元作为射击诸元使用。二维弹道修正弹在炮弹出膛后，可以通过纵向、横向弹道修正的方式消除射击诸元解算偏差，对诸元解算需求较常规炮弹低。一维弹道修正弹虽然具有纵向弹道修正能力，但因为在修正纵向弹道的过程中，横向弹道偏差和飞行时间均有较大变化，所以需要针对一维弹道修正弹设计合理的诸元解算方法，将缺省的弹道修正作为诸元解算的组成部分进行综合设计，避免一维弹道修正弹在提升纵向精度的同时，牺牲横向精度。

2 无控方式解算超越瞄准点射击诸元的偏差

在缺少成熟的一维弹道修正弹射击诸元解算方法的情况下，对一维弹道修正弹，一种普遍诸元求解方式如图1 所示。

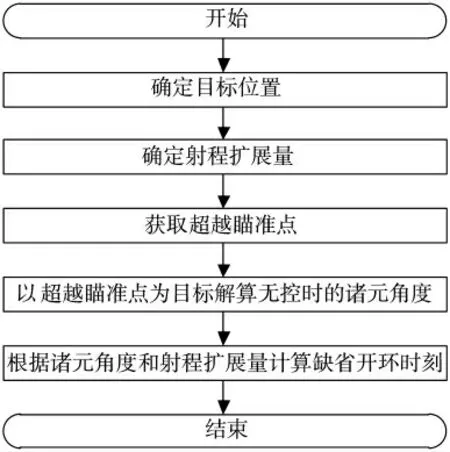
图1 一维弹道修正弹的简易诸元求解方法

这种简易求取一维弹道修正弹射击诸元方式的最大好处是将射击方位角、高低角与射程扩展量、缺省开环时刻分离。即在求解射击角度过程中，不考虑弹道修正，将一维弹道修正弹作为无控炮弹进行求解。这种方式无需设计新的诸元解算方法，可以充分继承现有的常规炮弹诸元解算方法。但根据这种方式计算得到射击诸元（方位角、高低角和缺省开环时刻）对应的理论弹道落点，与目标点在方位上存在较大的偏差，无法满足实际作战对诸元精度的要求。

2.1 标准条件下超越瞄准点射击诸元的方位偏差

一维弹道修正弹是一种陀螺稳定炮弹，弹道存在侧偏，且随射角增加而增大。标准条件下，炮弹无控时，一维弹道修正弹飞行时间和侧偏随射角的变化关系见图2，有控时的弹道侧偏与无控时的变化量见图3。

图2 飞行时间、侧偏与射角的关系

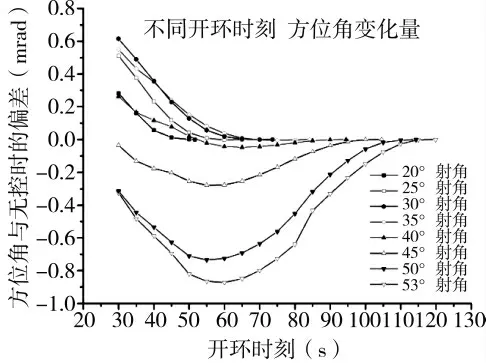
图3 不同开环时刻方位角的变化量

从图3 可以看出，标准条件下，一维弹道修正弹有控时的弹道偏流与无控时相比，最大变化已接近1 mrad，直接影响射击诸元的精度。

2.2 航行风对射击的影响

使用舰炮平台发射一维弹道修正弹时，因为舰船运动，需要在射击诸元解算时综合考虑舰船运动对炮弹飞行弹道的影响。舰船运动包含舰船的航行、摇摆、升沉等多个方面。其中，舰船航行对射击诸元的影响最大，行业内称其为航行风。航行风的影响与舰船的航速、航向（与射向偏差）、弹丸飞行时间等因素相关。同一射向、同一射角发射的一维弹道修正弹，开环时刻不同对应的弹丸飞行总时间也不同。不同开环时刻对应的飞行总时间的变化量见图4。根据舰船运动对炮弹飞行的影响，计算我舰以30 kn 速度航行，舰炮指向与航向夹角90°时，不同开环时刻对应的落点方位角偏差，计算结果见图5。从图5 可以看出，使用舰炮发射一维弹道修正弹，诸元解算时必须同步考虑开环时刻，否则仅航行风一项的影响就会导致一维弹道修正弹的理论弹道远离目标点。

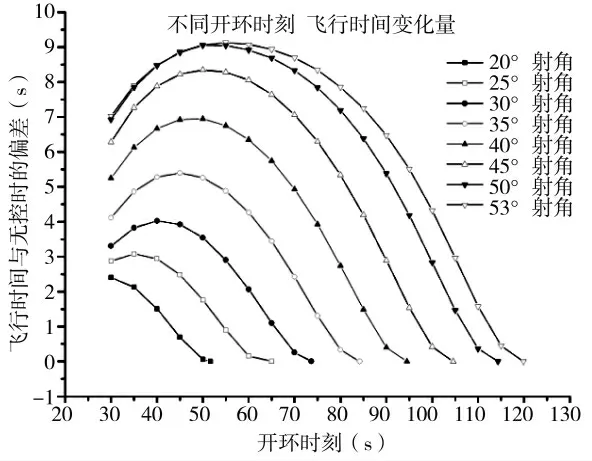
图4 不同开环时刻对飞行时间的影响

2.3 气象对射击的影响

气象因素是外弹道的重要影响因素之一，在常规炮弹射击诸元解算过程中，必需将气象因素纳入计算条件。对一维弹道修正弹，如果先以无控方式使用气象解算超越瞄准点对应诸元，再根据已计算出的诸元角度，以已经确定的射程扩展量为收敛目标，计算阻力环开环时刻。这样计算所得的缺省弹道，将仅能在射程上符合射程扩展量，在方位上无法保证命中目标。当气象条件比较复杂，与标准气象条件相差较大时，缺省弹道在偏流方向上的偏差将难以控制，不能满足实战使用需求。

3 舰炮一维弹道修正弹的射击诸元解算方法

3.1 一维弹道修正弹外弹道数学模型

这里采用文献［6］中的一维弹道修正弹弹道数学模型。

其中，

3.2 射程修正量及缺省开环时刻

对阻力环形式的一维弹道修正弹，射击前如何选取最佳射程扩展量目前尚没有最终研究结果。这里从无控弹道散布分布的角度出发，给出一个简易最佳射程扩展量ΔXdefault确定公式如下：

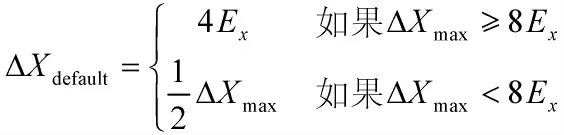
其中，Ex为无控时的射程X 对应的距离中间误差；ΔXmax表示射程X 时的最大修正距离，即全程不开环时射程和最早开环时射程之差。

根据上一节中分析，需将一维弹道修正弹的射击方位角、高低角、缺省开环时刻作为一个整体进行诸元解算［12-13］才能避免诸元解算模型中各影响因素的迭加误差。因为缺省开环时刻与射程扩展量一一对应，所以在诸元解算时，对缺省开环时刻和射程扩展量需满足以下两个约束：

1）以缺省开环时刻开环时，落点与目标点重合（距离和方位两个维度）；

2）同样的射击方位角和高低角，全程不开与缺省开环时刻的射程差为射程扩展量。

3.3 射击诸元解算方法

为描述求解过程方便，将一维弹道修正弹弹道方程简记为

即落点距离x，落点方位z 分别为射向Q、射角E、开环时刻tring的函数。

记

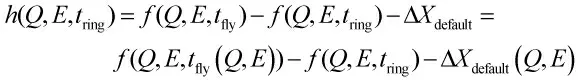
式（3）转变为

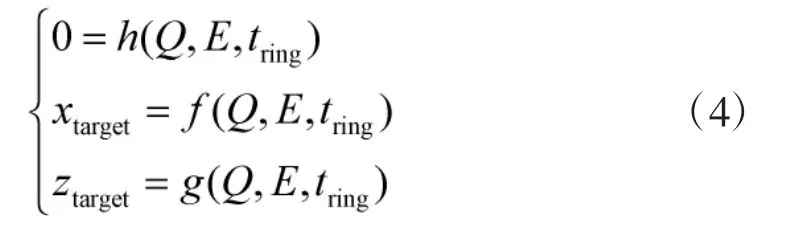
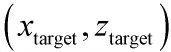
3.4 仿真计算结果

对正北向35.2 km 目标（对应射程扩展量800 m）进行仿真计算，无控方式解算超越瞄准点射击诸元的计算结果及落点偏差见表1，本文诸元解算方法的计算结果及落点偏差见下页表2。表1、表2 中的舰船运动1 为我舰以东北向20 kn 的速度航行，舰船运动2 为我舰以正东向30 kn 的速度航行，高空气象1 为某高海拔地区（海拔约1 400 m）某次夏日实测高空气象，高空气象2 为该地区某次冬日实测高空气象。

表1 无控方式解算超越瞄准点射击诸元的计算结果及落点偏差表

表2 本文诸元解算方法的计算结果及落点偏差表

注：无控方式解算超越瞄准点方法计算收敛条件为在射距方向上落点偏差小于0.01 m；本文诸元解算方法计算收敛条件为，缺省理论弹道落点与目标点偏差小于0.01 m。

从仿真计算结果中可以看出：在标准条件下，两种方法得到的缺省弹道落点与目标点偏差不大；考虑高空气象或我舰运动时，通过无控方式解算超越瞄准点方法得到的缺省弹道落点与目标点在偏流方向上的偏差很大。而通过本文诸元解算方法得到的缺省弹道落点，与目标点的偏差依然很小，可以满足作战使用需求。因此，本文中将射击方位角、射击高低角、缺省开环时刻作为一个整体进行诸元解算的方法是切实有效的，通过该方法得到的射击方位角、射击高低角可用于实战射击，缺省开环时刻可用于射击前的缺省状态装定。

4 结论

本文通过理论分析和仿真计算，说明了在一维弹道修正弹的诸元解算过程中，不能以无控方式解算超越瞄准点的方式进行射击诸元解算，否则在弹丸高速旋转带来侧偏、舰船运动、气象等诸多因素的影响下，解算出来的缺省弹道在方位上存在很大偏差。本文提出将缺省开环时刻和射击方位角、射击高低角作为一个整体进行诸元解算，通过该方法，消除了缺省开环时间一维弹道修正弹理论弹道在方向上的解算偏差，实现了在标准条件和非标条件下舰炮一维弹道修正弹射击诸元的精确解算。