如何理解“推理”
杨润歌 郜舒竹
【摘 要】推理是从一個命题判断到另一个命题判断的思维过程。其形式多种多样,包括演绎推理、归纳推理、类比推理、比例推理、协变推理以及变换推理等。推理能力贯穿于整个数学学习的过程,教师要帮助学生学会追根溯源,明晰算法背后的推理以及用联系的眼光看待推理间的不同形式,理解这些内容将有助于推理能力和辩证思维的发展。
【关键词】推理;比例推理;协变推理;变换推理;联系
《义务教育数学课程标准(2011年版)》(以下简称《课标》)中指出,在数学课程中,应当注重发展学生的推理能力。推理是人们日常生活和学习中经常使用的思维方式,它一般包括合情推理和演绎推理。在解决问题的过程中,两种推理的功能不同,相辅相成:合情推理用于探索思路,发现结论;演绎推理用于证明结论。《课标》中主要强调了演绎推理、归纳推理和类比推理,需要进一步思考的问题有:这几种推理形式之间的关系是什么?是否还有其他的推理形式?推理能力指怎样的数学能力?
一、推理
人的思维方式包括概念、判断和推理,其中推理(Reasoning)是指从一个命题判断到另一个命题判断的思维过程。[1]对于这种思维形式可以从形式逻辑推理和辩证逻辑推理进行深入认识。
(一)形式逻辑推理
形式逻辑包括演绎逻辑和归纳逻辑的内容,它指撇开具体的、个别的思维内容,从形式结构方面来研究命题。演绎逻辑是以演绎推理为基本内容的逻辑体系,其中演绎推理指由一般性知识为前提推出个别性知识结论的推理。而归纳逻辑是以归纳推理为基本内容的逻辑体系,其中归纳推理是从个别性知识为前提推出一般性知识结论的推理。
演绎推理与归纳推理均是由前提推出结论的过程,只不过演绎推理是由一般到特殊的过程,前者涵盖的知识内容要大于后者,按这一思维方式进行推理得出的结论必定是正确的,因此演绎推理亦可称为必然推理。相反,归纳推理是由特殊到一般的过程,其中的完全归纳推理为必然推理,不完全归纳推理则为合情推理。
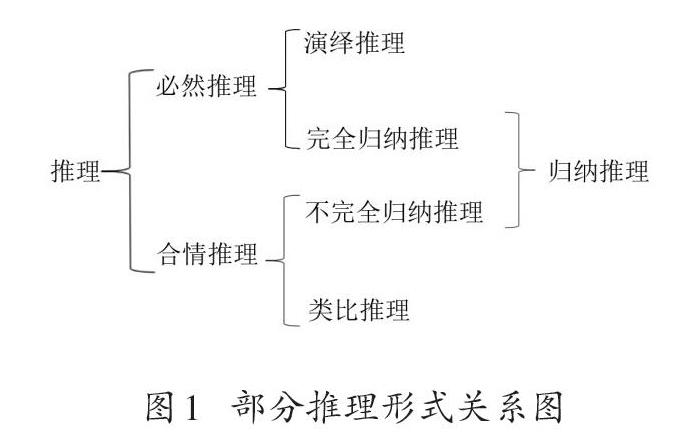
类比推理是根据两个或两类对象某些属性的相同,推出它们的其他属性也可能相同的推理。类比推理是一种合情推理,其可靠程度取决于“前提中确认的共同属性的多少以及共同属性和类推出来的属性的关系是否密切”。[2]因此,按必然推理与合情推理的分类标准对《课标》中的相关内容进行整理,如图1所示。
《课标》中谈及“教师在教学过程中,应该设计适当的学习活动,引导学生通过观察、尝试、估算、归纳、类比、画图等活动发现一些规律,猜测某些结论,发展合情推理能力”。但图1的推理关系表明,归纳推理并非全部属于合情推理的范围,而仅指归纳推理中的不完全归纳推理。
在形式逻辑的学科视野中,推理前提的真实性是由各门具体科学给定的,是各门具体科学研究的对象,形式逻辑本身是无从证实其前提内容真实性的。[3]也就是说形式逻辑推理是从具体推理中抽象出推理形式进行研究,只要满足其同一律、矛盾律和排中律即可,无须考虑内容。这就使得《课标》中关于“通过实例使学生逐步意识到,结论的正确性需要演绎推理的确认”的说法,更值得细细推敲,即进行演绎推理的前提不一定都是正确的。
(二)辩证逻辑推理
辩证逻辑不是关于思维的外在形式的学说,它研究概念的矛盾和转化,是现实的矛盾运动在思维运动中的反映。[4]概念间的组合会形成命题或判断,而推理又是从一个判断到另一个判断的过程,因此概念、判断和推理三者之间环环相扣。辩证逻辑将概念中的矛盾继续延伸到推理中。矛盾的普遍性决定了当以辩证的眼光看待问题时,任何事物都是对立统一的存在,也就是矛盾具有客观性,这种矛盾是无法消除或避免的。
在形式逻辑中也存在矛盾律,是指某一命题或判断不能既为真又为假。只要遵守这条规律,注重命题或判断的描述,矛盾是可以避免的,这一点与辩证逻辑有所不同。《课标》关于“证明命题时,应要求证明过程及其表述符合逻辑,清晰而有条理”这一表述中的“符合逻辑”是符合形式逻辑。一是指推理形式符合规律,主要是指矛盾律。若按形式逻辑理解矛盾律自然可以避免,但若以辩证思维来考虑问题,矛盾一定存在就不合乎逻辑了。二是忽略了推理内容。比如人教版小学数学四年级下册出现的“鸡兔同笼”问题,其中一种解题想法是“使鸡抬起一只脚”以及“兔抬起两只脚”,进而推理出鸡兔各为多少。[5]这一过程中出现的“是鸡”“非鸡”与“是兔”“非兔”的内容情境是存在矛盾的,显然也不符合形式逻辑。
形式逻辑推理与辩证逻辑推理各有其特性,二者相辅相成,可以从形式与内容两个角度以辩证思维看待推理形式。《课标》中将合情推理与演绎推理作为两种相辅相成的推理形式,强调“‘证明的教学应关注学生对证明必要性的感受,对证明基本方法的掌握和证明过程的体验”。此处似乎将推理能力的发展寄托于证明题,并在附录中出示了相关例题(参见《课标》例62)。事实上,推理不仅存在于证明题中,在应用题的求解、知识点的学习等内容中均有体现,且推理形式不拘泥于《课标》中所谈及的。
二、多样性
推理的教学往往不会孤立存在于某一板块内容与某几种形式之间,因此除《课标》中谈及的演绎推理、归纳推理和类比推理外,推理的形式是多种多样的。
(一)比例推理
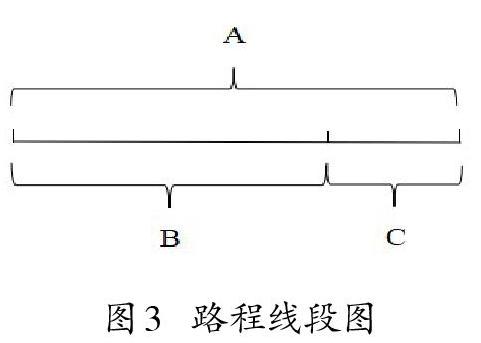
比例推理(Proportional Reasoning)是关于数量关系的思考,要求同时对几个数量或值做出比较。[6]在小学数学教科书中比例推理常以缺失值的形式呈现。如“小明骑行4千米用时20分钟,小刚同速骑行12千米需要多长时间?”对于该问题,可以从以下三个角度思考。其一“一份是多少”的策略,根据小明的骑行信息可知二人的骑行速度为1分钟行驶[15]千米,或行驶1千米用时5分钟,此时再运用速度、时间与路程的数量关系即可求得小刚的用时。其二“倍数有多少”的策略,小刚比小明多走了3倍,所用时间亦为3倍关系。其三“交叉相乘”策略,利用二者同速的条件列方程求解。[7]前两种策略是建立在学生生活经验之上的一种直观方法,而第三种策略是学生惯用的一种算法,只要遇到相似形式的方程就会做出的一种操作,因此,需要进一步思考这种算法背后的算理是什么。
因此,数学教学中培养的推理能力,应当是用联系与发展的眼光看待问题的综合能力。
综上,推理作为一种思维形式,要将推理的形式结构与内容结合起来辩证地加以认识。在知识学习以及问题解决过程中存在多样的推理形式,它们之间相互联系,并不是彼此割裂的对立面。
参考文献:
[1]史宁中.数学基本思想18讲[M].北京:北京师范大学出版社,2016:119.
[2][4]余源培.简明哲学辞典[M].上海:上海辞书出版社,2005:246,223.
[3]贺善侃.辩证逻辑和形式逻辑推理研究比较[J].重庆理工大学学报(社会科学版),2013(9):47-52.
[5]郜舒竹.鸡兔同笼问题中的辩证思维[J].课程·教材·教法,2019(9):88-93.
[6]李晓东,江荣焕,钱玉娟.中小学生对比例推理的过度使用[J].数学教育学报,2014(6):73-77.
[7]Kathleen C, Thomas P. Proportional Reasoning[J]. The Mathematics Teacher,1993, 86(5):404-407.
[8]Marilyn C, Sally J, Edward C. Applying Covariational Reasoning While Modeling Dynamic Events: A Framework and a Study[J]. Journal for Research in Mathematics Education,2002, 33(5):352-378.
[9]Simon M A. Beyond Inductive and Deductive Reasoning: The search for a sense of knowing[J]. Educational Studies in Mathematics,1996, 30(2):197-210.
[10]Kuo-Liang Chang. Redeem Reasoning[J]. Mathematics Teaching in the Middle School, 18(7):396-399.
(首都師范大学初等教育学院 100048)

