顾及频间钟差的BDS/GPS三频非组合精密单点定位方法

赵 庆，高成发，潘树国，高 旺，夏 炎

（1.东南大学交通学院，南京 210096；2.东南大学 仪器科学与工程学院，南京 210096）

随着BDS、Galileo、QZSS等系统的发展，多系统多频成为近年来卫星导航领域的研究热点，尤其是多频观测值引入的各项偏差，譬如差分码偏差（Differential Code Bias,DCB）、系统间偏差（Inter System Bias,ISB）等[1-3]，为此International GNSS Service（IGS）成立了专门的偏差标定工作组（Bias and Calibration Working Group,BCWG）。目前，各分析中心一般采用 GPS L1/L2、BDS B1/B2的无电离层组合模型进行精密钟差估计，由此得到的钟差产品包含无电离层组合的卫星端硬件延迟[4]，可直接用于L1/L2、B1/B2双频精密单点定位（Precise Point Positioning,PPP）。当采用L5或 B3观测值进行精密单点定位时，无法直接采用L1/L2或B1/B2无电离层组合估计得到的卫星钟差，需要额外处理L1/ L2与L5、B1/B2与B3之间的偏差，即频间钟差（Inter-Frequency Clock Bias,IFCB）。

关于IFCB，国内外学者已陆续开展了相关研究。文献[5]初步分析GPS Block IIF卫星IFCB的时变特性，指出了其部分原因是由于卫星受太阳光照内部温度产生变化而导致。在解算策略和建模方面，文献[6]提出了一种基于历元间差分的 IFCB解算策略，并采用谐波函数进行建模，但未进行相应的PPP验证。为此，文献[7][8]分别针对GPS和BDS的IFCB，在建模的基础上，采用两种无电离层组合的方法进行了静态 PPP验证，定位精度提高 10%～20%左右。由于无电离层组合PPP难以适应多频数据统一处理，而基于原始观测值的非组合PPP则可以兼容多频观测值，近年来，有不少学者对非组合PPP展开研究。文献[9][10]提出了一种BDS三频非组合PPP模型，不过并未考虑IFCB的影响；文献[11]则初步分析了IFCB在GPS非组合PPP中的应用。

上述研究并未涉及IFCB对BDS非组合PPP的影响，且相关的验证实验以静态PPP为主。基于此，本文给出了BDS/GPS三频非组合PPP的函数模型以及对应的IFCB改正方法，并通过Multi-GNSS Experiment（MGEX）监测站的实测数据，分析了单BDS、单GPS和BDS/GPS组合模式下，IFCB对静态以及动态PPP的影响。

1 IFCB估计方法

IFCB通常采用两个无电离层组合作差的方法估计，以BDS为例，B1/B2和B1/B3两个无电离层组合相位观测方程作差可得：

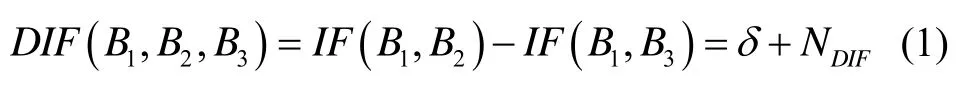
式中，I F （ B1,B2）和 IF（ B1,B3）分别为B1/B2和B1/B3的无电离层组合观测值，D IF（ B1,B2,B3）为无电离层组合观测值之差，δ为 IFCB，NDIF为包含模糊度以及接收机硬件延迟的常数项。需要注意的是，式(1)中与频率相关的误差（如天线、相位缠绕）已通过相应模型进行改正，从而可以提取纯净的IFCB。

为了消除常数项 NDIF，在无周跳的连续观测弧段，进行历元间差分：

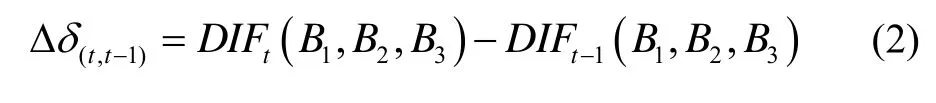
通过单站即可计算Δδ(t,t-1)，不过考虑到观测噪声以及单站解算的偶然性，通常对某一历元多个测站的Δδ(t,t-1)进行加权平均，以提高其稳定性，具体如下：

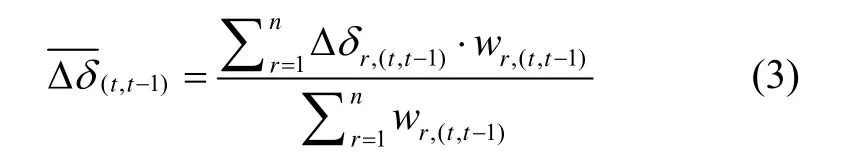
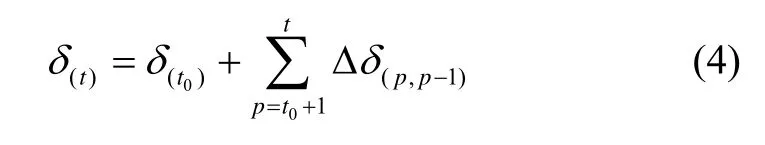
式中，0()tδΔ 和()tδΔ 分别为参考历元与当前历元的IFCB。GPS的IFCB估计方法类似。

2 顾及IFCB的三频非组合PPP方法

非差伪距与载波的原始观测方程为：

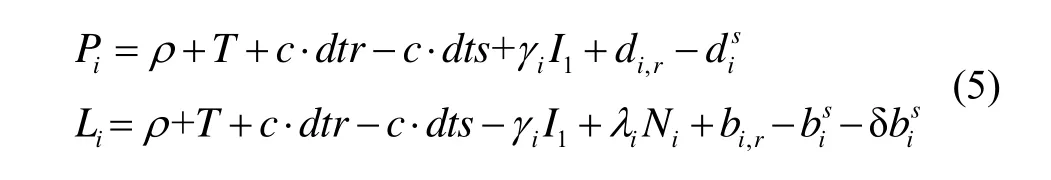
其中，i表示频率，s和r分别表示卫星和接收机，P和L分别为伪距与载波观测值，ρ为站星距，T为对流层延迟，c为光速，dtr和dts分别表示接收机和卫星钟差，I为电离层延迟，γ表示与频率相关的系数，λ和N分别为波长和对应的整周模糊度，d表示时变稳定的伪距硬件延迟，b表示时变稳定的相位硬件延迟，δb表示随时间变化的相位硬件延迟。

由于待估参数较多且相互耦合，无法同时全部估计，通常采用重参化的方法解耦，譬如，接收机钟差吸收B1/B2无电离层组合的接收机端伪距硬件延迟，而电离层则与相应DCB参数进行整合，具体如下：

自从1998年我国高等学校进行创新创业教育以来，高校的创新创业教育得到了迅速发展。目前，随着互联网经济的发展以及“双创”的推进，全国各个高校都在积极开展创新创业教育，目的在于培养学生的创新创业知识和创新创业能力。然而目前大部分地方高校的创新创业工作还处于摸索阶段，主要表现在大学生创新创业意识不强、积极性不高、参与度不高、缺少创新思维等多个方面。本文以湖北省属高校大学生创业教育为例，在调研的基础上，拟对湖北省属高校大学生创业教育现状进行评估并对以后的改革方向进行研究。

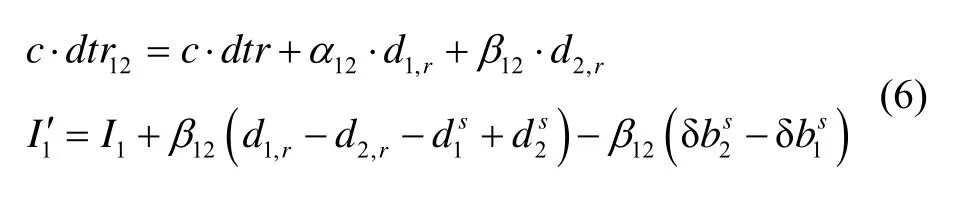
式中，dtr12和I′1分别表示重参化的接收机钟差和电离层参数，α12和β12表示B1/B2无电离层组合系数。

同时，顾及精密钟差自身已经吸收了无电离层组合的卫星端硬件延迟：

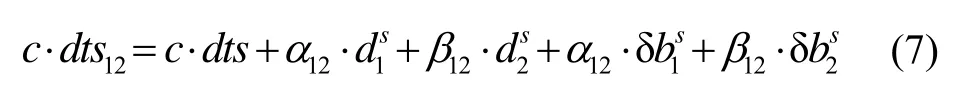
式中，dts12即为由分析中心提供的实际卫星钟差。

通过上述重参化，可以得到BDS三频非组合PPP的伪距观测方程如下：

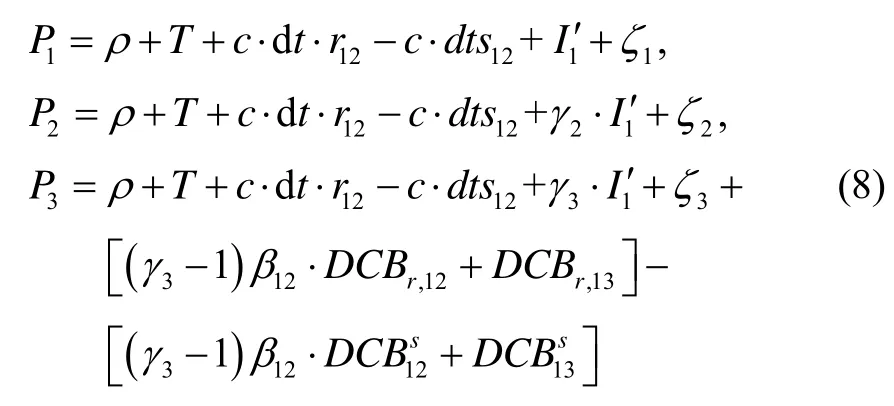
式中：D CBr,12和 D CBr,13分别表示接收机端B1/B2和B1/B3的DCB；和分别表示卫星端B1/B2和B1/B3的DCB；ζi(i = 1,2,3)表示残余的硬件偏差，具体如下：

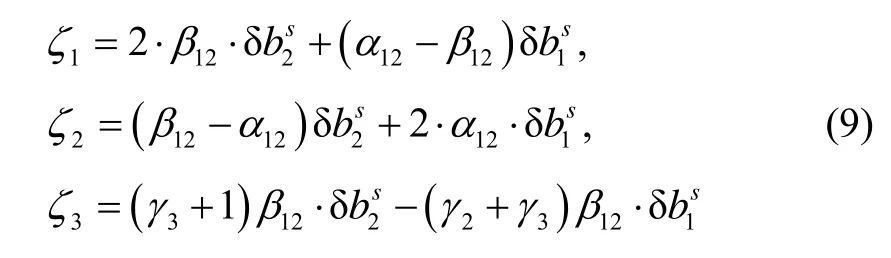
式中，卫星端的 DCB项可由事后产品改正，而接收机端的 DCB项则作为附加的参数进行估计。考虑到与相位观测值相比，伪距的权值较低，观测方程中残余的硬件偏差ζi无需额外改正。

通过保持伪距方程与载波方程待估参数一致，类似地，可以化简得到载波的观测方程：

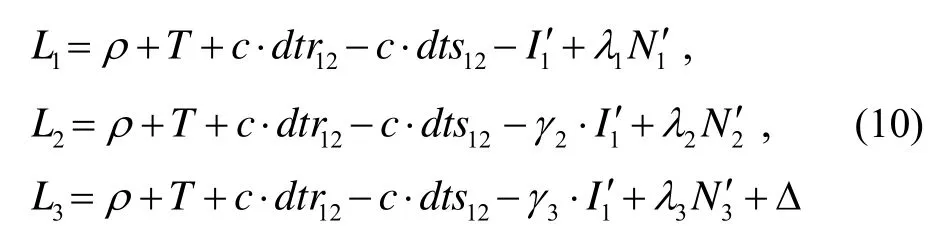
式中：N′i表示相应频率的浮点模糊度，其中吸收了时变稳定的硬件延迟；Δ为与传统双频非组合PPP相比，需要额外改正的相位硬件偏差，即非组合的IFCB，其具体形式为：

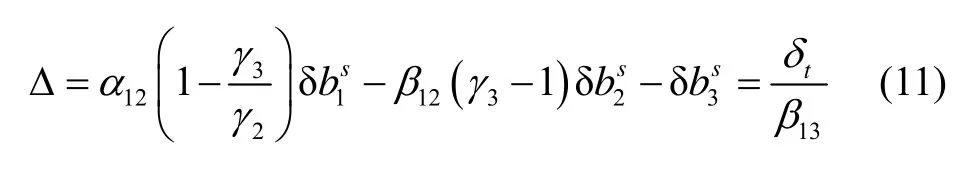
式中，δt即为之前通过历元间差分方法计算得到的IFCB，β13为B1/B3无电离层组合系数。

通过上述重参化过程，可以确定BDS三频非组合PPP的观测模型，GPS的模型推导类似。在进行BDS和GPS组合定位中，由于不同系统在接收机端通道时延不同，需要额外估计1个系统间偏差参数。

3 实验结果与分析

为了保证IFCB序列的连续性，选取分布于全球的 184个 MGEX观测站，用连续 7天（2018年DOY140～146）的观测数据解算 BDS/GPS的 IFCB，数据采样率为30 s，站点分布如图1所示。数据处理中，高度截止角设为10°，采用IGS提供的多系统DCB产品改正B3/L5频点的卫星端DCB，精密轨道、钟差产品由德国地学研究中心（GeoForschungsZentrum Potsdam,GFZ）提供，并采用对应的天线改正。其中：GPS卫星端和接收机端的天线采用 IGS发布的IGS14.atx文件进行改正，由于接收机端缺少L5频点参数，故采用L2频点天线参数对L5观测值进行改正；BDS GEO卫星端天线改正采用名义值，非GEO卫星采用由欧洲航天局（European Space Agency,ESA）[12]提供的参数进行改正，由于现阶段BDS缺少接收机端天线改正，为了与精密产品的数据处理策略保持一致，故采用GPS L1/L2/L5的天线参数对BDS B1/B2/B3观测值进行改正。为了保证有足够的可视BDS卫星数，选取分布于亚太地区的 3个连续跟踪站（KARR、KAT1、MRO1）进行实验验证（如图1所示），以及分析IFCB对三频非组合PPP定位的影响。

3.1 IFCB时变特性

选取每天的零点作为参考历元进行IFCB的计算，可以得到基于参考历元的IFCB序列，图2和图3分别是GPS和BDS连续7天的IFCB时间序列。由图2可以看出，GPS卫星的IFCB随时间规律性变化，周期性明显，约为1个恒星日，不同天之间重复性较好，其变化量级由几厘米到十几厘米不等，譬如G24卫星，最大可超过 15 cm，这对于精密定位而言是不可忽略的一项误差。由图3可以看出，BDS GEO（图3中洋红色）和IGSO（图3中蓝色）卫星的IFCB与GPS卫星类似，均可以看到较为明显的周期性变化，其中：C02和C05由于观测数据质量差，周跳频繁，影响了最终的IFCB解算结果，故效果略差于其余GEO卫星；MEO（图3中绿色）卫星IFCB变化并无明显周期性规律。总体而言，BDS所有卫星的IFCB变化量级比GPS小，一般不超过3 cm，且GEO卫星变化量级略大于IGSO和MEO卫星。

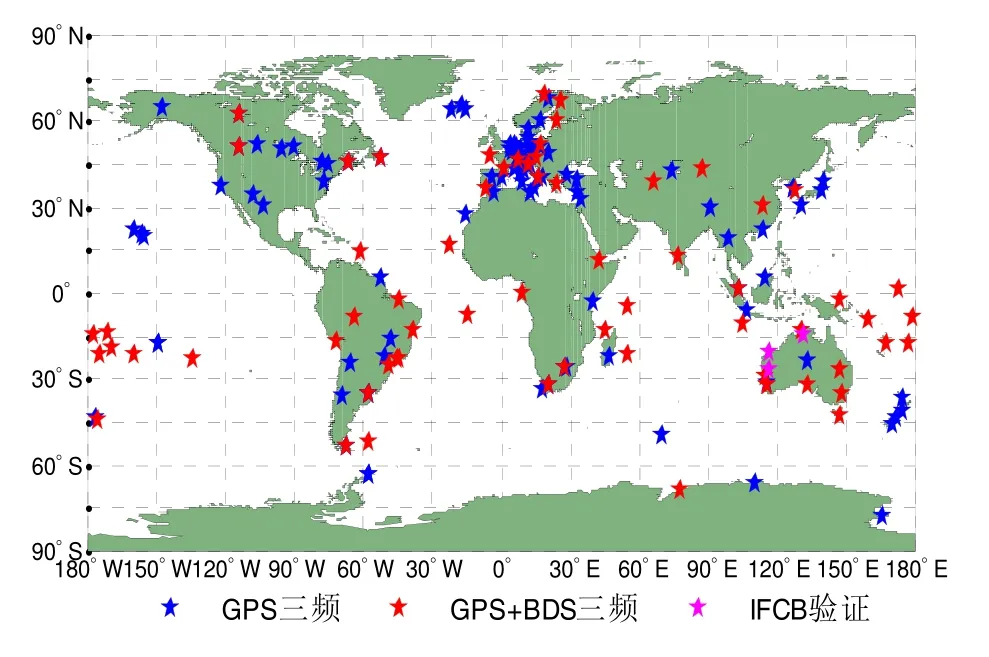
图1 MGEX站点分布图Fig.1 Distribution of MGEX site

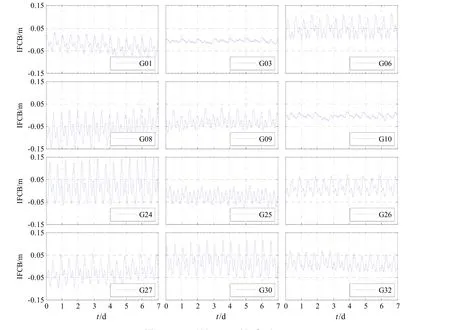
图2 GPS卫星IFCB时间序列Fig.2 Time series of GPS satellite inter-frequency clock bias

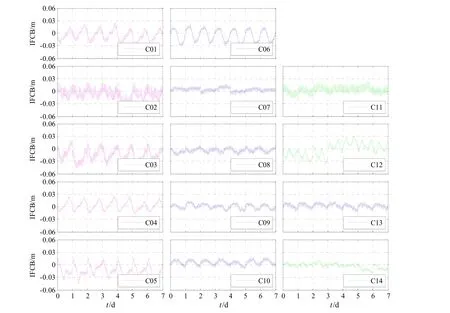
图3 BDS卫星IFCB时间序列Fig.3 Time series of BDS satellite inter-frequency clock bias

3.2 IFCB 对静态PPP 的影响

以MRO1 测站DOY142 的结果为例，图4 分别给出了IFCB 改正前后单BDS 和单GPS 三频PPP 的误差曲线。对于单BDS，由于其本身IFCB 变化量级小，且目前GEO 卫星轨道精度差，IFCB 改正对静态PPP的结果影响较小，如图4(a)所示。与不改正IFCB 相比，IFCB 改正后，北向（N）误差变化曲线与不改正IFCB 基本重合，在东向（E）、天向（U），前6 h 可以看到定位精度有小幅提高。不改正IFCB，单BDS N、E、U、3D 方向定位精度分别为3.8 mm，6.6 mm、24.2 mm和25.4 mm，改正IFCB 后，精度为3.8 mm、6.1 mm、21.9 mm、23.0 mm，E、U 方向精度有小幅提升，点位精度提高9.1%。对于单GPS，由于其IFCB 变化量级较大，IFCB 改正前后，N、E、U 方向的定位误差改善明显（如图4(b)所示），不改正IFCB，N、E、U、3D 方向定位精度分别为10.2 mm、10.2 mm、28.1 mm、31.6 mm，改正IFCB 后，定位精度提高为2.5 mm、2.4 mm、3.9 mm、5.2 mm，点位精度提高83.4%。

除观测噪声外，一些非模型化的误差（譬如IFCB）会体现在观测方程验后残差中，图5 中(a)～(d)分别给出了MRO1测站GPS 卫星L5 频点和BDS GEO/IGSO/MEO 卫星B3 频点的载波相位验后残差序列分布。如图5 所示，不加IFCB 改正，GPS 卫星L5 以及BDS卫星B3 频点的相位残差体现出明显的系统性误差，GPS 最为明显，GPS 卫星和BDS GEO/IGSO/MEO 卫星相位残差标准差分别为0.80 cm、0.33 cm、0.28 cm、0.26 cm；改正IFCB 后，这一系统性误差得以消除，相应的相位残差标准差分别为0.20 cm、0.15 cm、0.19cm、0.21 cm，分别减小了75.0%、54.5%、32.1%、19.2%。GPS 卫星的改善效果最为明显，这与GPS 自身IFCB量级较大有关。

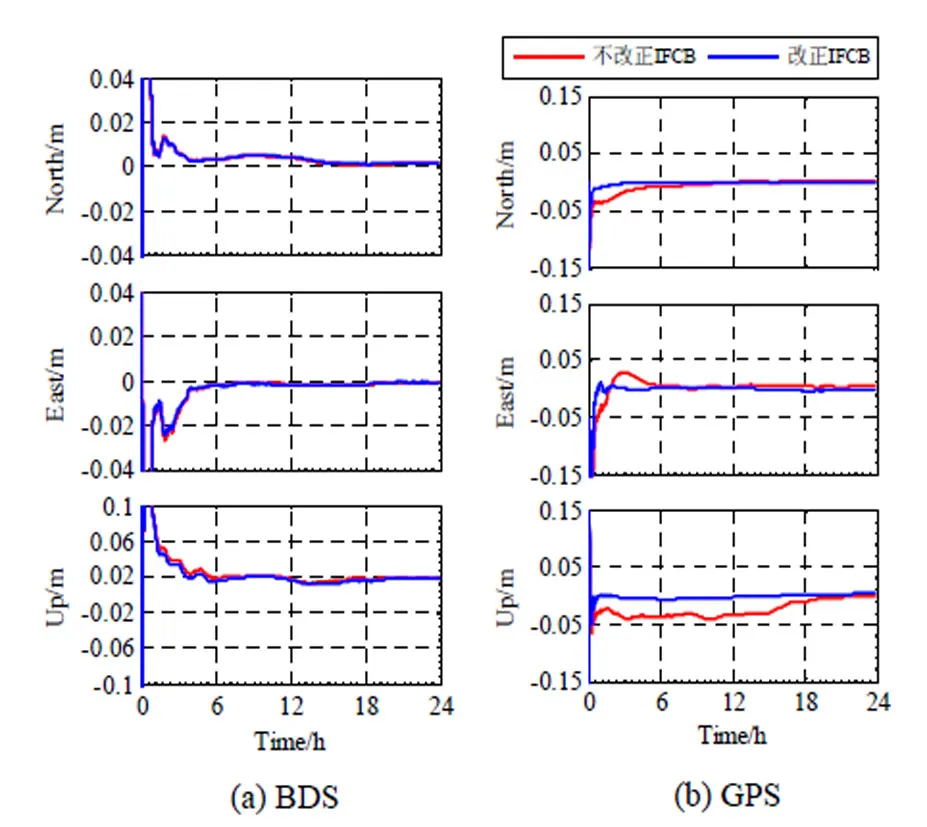
图4 非组合静态PPP 定位误差曲线Fig.4 Error of uncombined static PPP

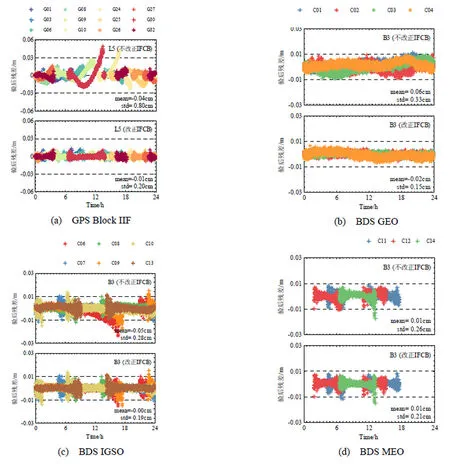
图5 MRO1 测站非组合PPP 相位残差序列Fig.5 Uncombined PPP phase residuals of MRO1

3.3 IFCB对动态PPP的影响

分别进行单 BDS、单 GPS、BDS/GPS组合这 3种方案的动态PPP实验，坐标的过程噪声均方误差设为60 m，将每个测站24 h数据分成3个时段进行解算。限于篇幅，图6仅给出了KAT1测站的点位误差曲线，详细统计结果见表1。

由图6(a)可知，IFCB对单BDS动态PPP的定位结果影响很小，IFCB改正前后，定位精度基本一致；由图6(b)、6(c)可知，IFCB对单GPS和BDS/GPS双系统组合动态 PPP的定位结果有较大改善。对于单GPS，IFCB改正前N、E、U方向定位精度分别为2.7 cm、5.1 cm、8.0 cm，IFCB改正后N、E、U方向定位精度提高为 1.0 cm、1.8 cm、3.2 cm，点位精度提高59.6%；对于 BDS/GPS双系统动态PPP，IFCB改正前N、E、U方向定位精度分别为1.4 cm、2.1 cm、4.6 cm，IFCB改正后N、E、U方向定位精度提高为0.6 cm、0.9 cm、2.1 cm，点位精度提高54.7%。

总体而言，单BDS动态PPP的定位性能整体差于单GPS，通常需要约2h的时间才能达到10 cm的精度，BDS/GPS双系统组合可视卫星数多，定位的精度和稳定性优于单BDS和单GPS。

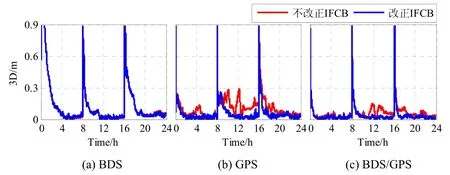
图6 非组合动态PPP定位误差曲线Fig.6 Error of uncombined kinematic PPP

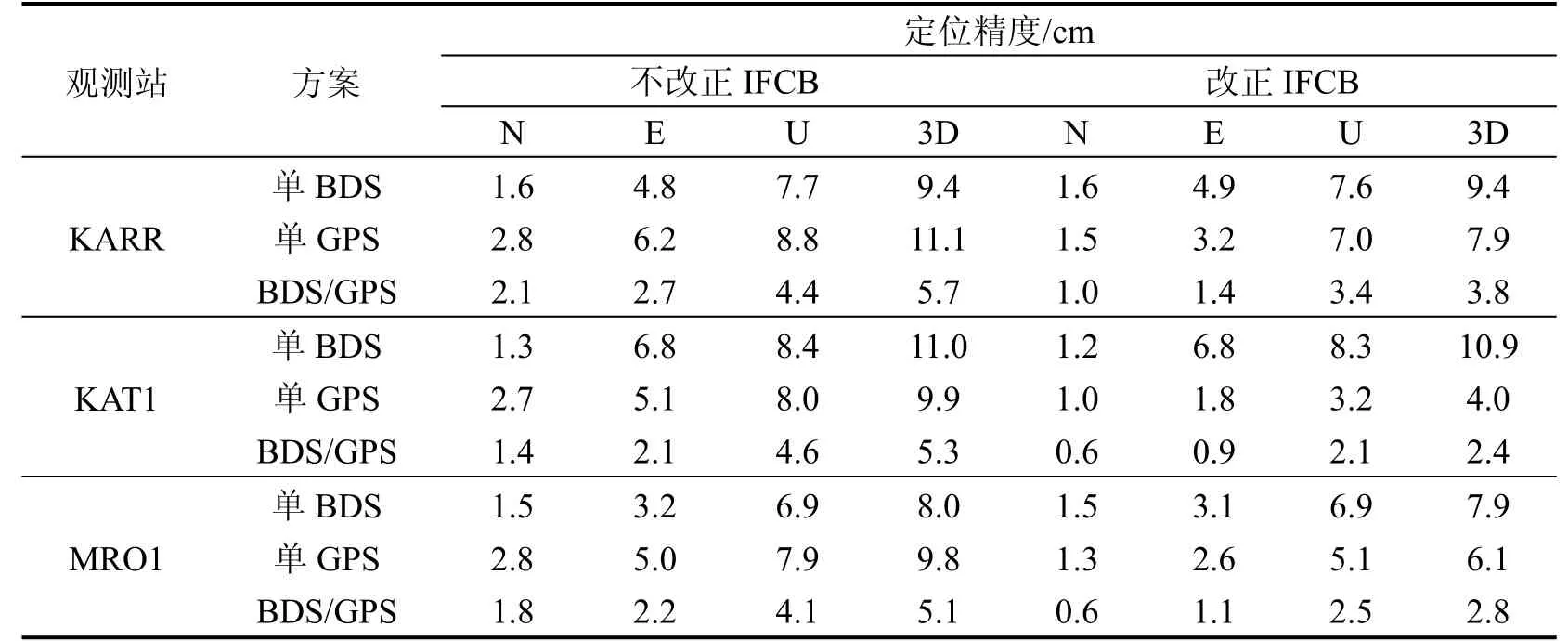
表1 三频非组合动态PPP精度统计Tab.1 Accuracy statistics of tripe-frequency uncombined kinematic PPP

4 结 论

本文针对传统钟差产品无法直接应用于多频精密单点定位的问题，提出了基于几何无关模型的 IFCB估计方法，并进一步推导了顾及IFCB的三频非组合PPP模型。通过全球的实测数据进行实验，研究表明，考虑IFCB改正后，单GPS静态PPP定位精度提高83.4%，单GPS和BDS/GPS双系统组合动态PPP定位精度分别提高59.6%和54.7%，有效解决了IFCB对多频定位结果产生的系统性偏差问题，实现了传统钟差产品与多频精密定位的统一。