基于MCC的鲁棒高阶CKF在组合导航中的应用

卢 航，郝顺义，彭志颖，黄国荣

空军工程大学 航空工程学院，西安710038

1 引言

捷联惯导系统（SINS）通过惯性测量元件（IMU）测量运载体相对于惯性系的运动信息，经过导航计算机解算得到运载体的姿态、速度、位置等导航信息，是一种具有较强自主性的导航系统，其具有短时导航精度高，但是长时间导航精度低的特点。全球定位系统（GPS）是一种卫星导航系统，它可以精确的提供运载体的速度、位置等导航信息，其长时间导航精度高，但是战时自主性较差。SINS/GPS组合导航是一种结合两种导航系统优点的导航方式，可以提高导航系统的整体性能[1]。

在组合导航系统定位中，高精度的滤波算法对导航定位的解算精度有重要影响[2]。卡尔曼滤波（KF）是最小均方差条件下的线性最优滤波器，其可以较好地处理高斯噪声条件下线性模型的状态估计问题。然而，非线性问题在实际中更为普遍，组合导航系统是典型的强非线性系统，此时非线性滤波算法成为提高组合导航精度的关键。扩展卡尔曼滤波器（EKF）采用对非线性函数进行一阶泰勒展开的原理，对非线性函数进行近似，显然其会引入线性化截断误差，滤波精度只能达到一阶，同时求取繁琐的雅各比矩阵会造成较大的计算量和较低的数值稳定性[3]。粒子滤波（PF）是一种无需对状态方程近似、也无需对噪声统计特性进行假设的的滤波算法，但是通常需要巨大的粒子数以牺牲计算量换取满意的滤波精度，同时重要性概率密度的选择也是一个难题。目前，较为常用的非线性滤波算法为高斯近似求和滤波，不同于EKF对状态方程近似的思想，其认为近似后验概率密度比近似非线性函数更容易，通过一定的规则精心选取采样点和权值达到状态估计的目的，其中以无迹卡尔曼滤波（UKF）和容积卡尔曼滤波（CKF）为代表，两者无需计算雅各比矩阵且精度高于EKF[3-4]。文献[4]研究对比了UKF和CKF的滤波精度和数值稳定性问题，指出CKF的滤波精度可以精确到三阶，同时UKF的数值稳定性要低于CKF。文献[5]在传统CKF 的基础上，提出了利用高容积规则计算高斯求和积分的HCKF算法，其滤波精度可以达到五阶。

在实际物理系统中，量测信息通常会受到外部环境、仪器故障等因素的干扰，此时量测噪声不再满足高斯分布的前提假设[7-8]，所以基于噪声服从高斯分布假设法是解决这一问题的有效方法[18]，文献[19]将MCC 和KF 结合提出了一种基于MCC 的鲁棒KF 算法，并且通过目标跟踪仿真实验验证了其可以较好的应对高斯分布附近存在对称干扰问题。为了改善组合导航算法的滤波精度和鲁棒性，本文将MCC 方法应用于HCKF 算法，利用MCC对量测信息进行重新构建，提出一种基于MCC的鲁棒HCKF滤波算法。当量测噪声表现为高斯混合分布时，该算法在鲁棒性、滤波精度等方面优于传统CKF，通过SINS/GPS 组合导航系统验证了所提算法的优越性。

2 SINS/GPS组合导航系统模型

2.1 组合导航系统状态方程

记惯性坐标系为i 系，地球坐标系为e 系，载体坐标系为b 系，选取当地地理坐标系即“东、北、天”坐标系为导航坐标系n 系，SINS 计算所得的导航坐标系为p系。由于SINS 受各种误差源的影响，导致导航计算机所计算出来的p 系与n 系之间存在着失准角误差ϕ=[ϕxϕyϕz]T，它表示n 系转至p 系的一组欧拉角，转动顺序定义为ϕz、ϕx、ϕy。那么从n 系至p 系的坐标变换矩阵为：

用GPS/SINS松组合导航系统为滤波模型，以SINS的姿态、速度、位置、陀螺零偏和加速度计零偏的误差方程作为非线性滤波模型的状态方程，以SINS 和GPS 输出的速度、位置误差作为量测值。SINS 的姿态、速度、位置非线性误差方程为[21]：

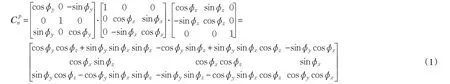
的滤波算法不能表现出良好的滤波性能。针对高斯分布附近存在对称干扰问题，Huber提出了M估计同时针对非高斯噪声的问题给出了Huber 方法[9-10]，Huber 用一种基于范数的混合代价函数取代基于l2范数的代价函数来处理干扰干高斯分布的问题，其鲁棒性要优于基于l2范数的估计方法[11]，文献[12-16]提出了基于Huber的鲁棒滤波算法并在目标跟踪和无人机相对导航中取得了成功应用，但是Huber 在面对非高斯噪声时，其量测更新过程仍然会受到较大的影响，最终导致滤波精度下降[17]。除此之外，近几年提出的基于最大相关熵MCC（Maximum Correntropy Criterion）的鲁棒滤波算

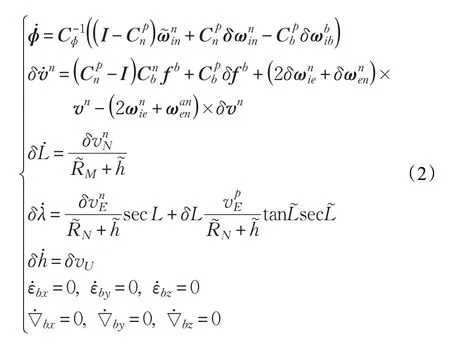
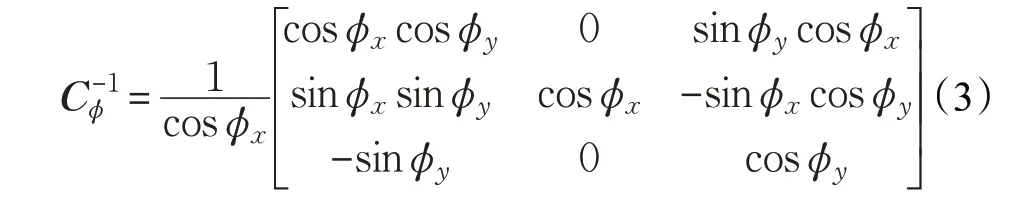
定义15 维状态向量X=[ϕxϕyϕzδvxδvyδvzδLδλδh εbxεbyεbz∇bx∇by∇bz]T，可由式（2）构成SINS/GPS 组合导航系统的状态方程：

式中f()· 为非线性函数，w 为系统噪声。

2.2 组合导航系统量测方程

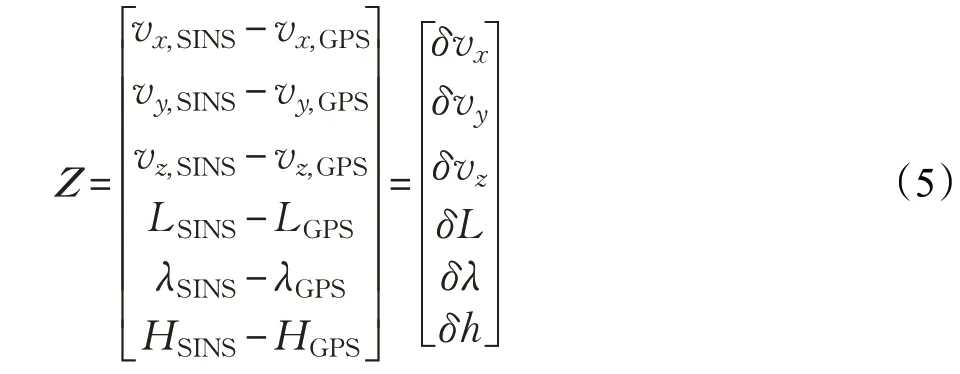
取SINS 和GPS 输出的速度、位置信息之差作为滤波器的量测值，即

那么组合导航系统的量测方程为：

3 基于MCC的鲁棒高阶CKF算法

3.1 最大相关熵

假设两个随机变量x,y ∈R，二者联合概率密度函数为pxy(x,y)，定义相关熵为：

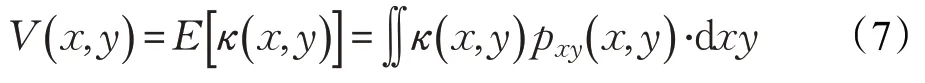
式中，E 表示期望，κ( x,y )表示高斯核函数，具体表达式为：

其中e=x-y，σ 为核宽且σ ＞0，在实际应用中，通常只能获得有限的数据并且联合概率密度是未知的，可以用一系列的采样点得到V( x,y )的近似解[17]，此时式（8）可以写为：

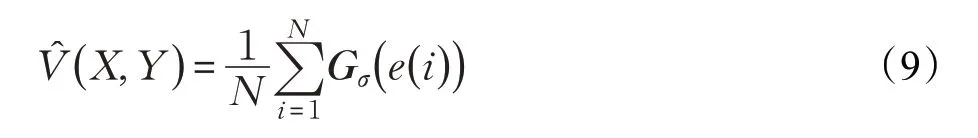
图1为σ=1 时的相关熵示意图，可以发现相关熵衡量两个随机变量之间的广义相似程度，误差e 的贡献会随着核宽σ 的变化出现不同程度的指数形式的衰减，当e=0 时κ( x,y )=1 取最大值。定义基于MCC 准则的代价函数为：

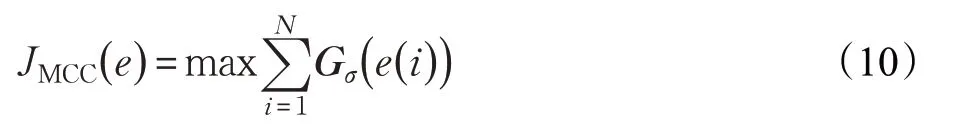
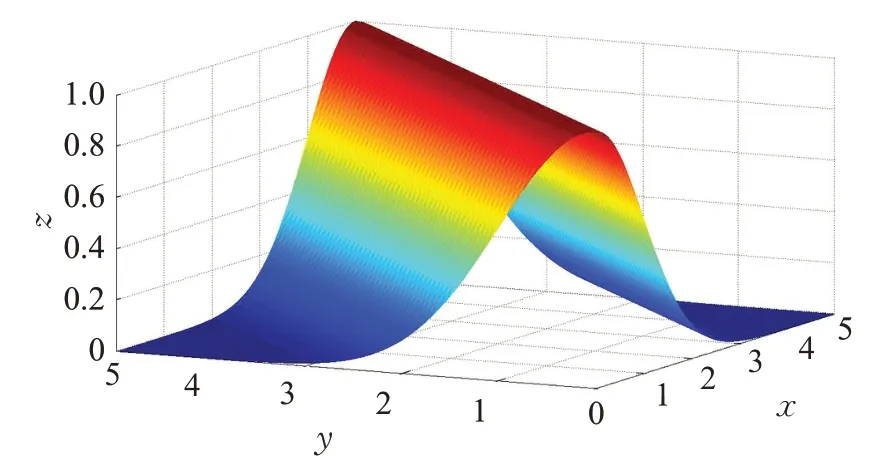
图1 相关熵κ( x,y )示意图

3.2 高阶容积卡尔曼滤波

（1）滤波器初始化

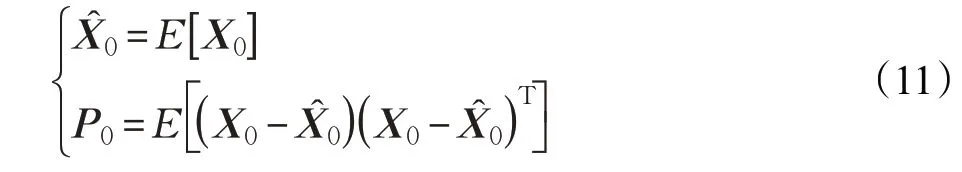
（2）时间更新过程

①计算容积点Xi,k-1|k-1( i=0,1,…,2n2)：采用具有更高数值稳定性的奇异值分解（SVD）代替了传统的Cholesky 分解，该分解方法可以更好地解决协方差矩阵病态条件的问题，使得整个算法具有更高的数值稳定性和滤波精度，对协方差矩阵Pk-1/k-1使用SVD 分解，即

式中，n 为系统的状态维数，ei`表示n 维单位向量，第i个元素为1，的具体表达式为：

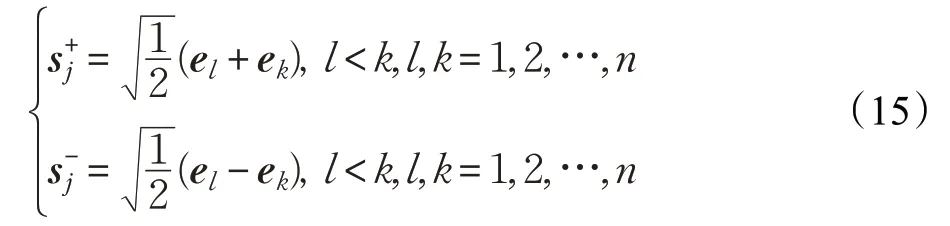
式中，ωi为容积点的权值，如下式所示：

④计算k 时刻的预测误差协方差阵Pk/k-1：

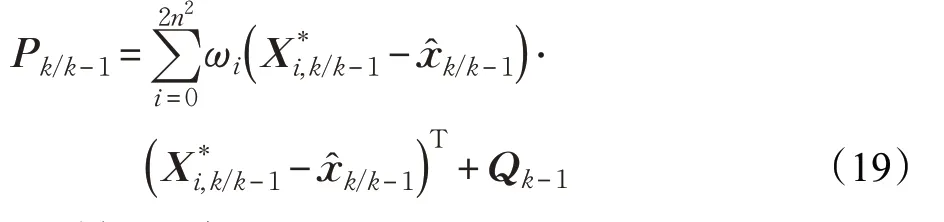
（3）量测更新过程

①计算更新后的状态容积点Xi,k|k-1：

其中，Pk/k-1=Sk|k-1(Sk|k-1)T。

②计算经过量测方程传递的容积点Zi,k|k-1：

③计算k 时刻的测量预测值ẑk|k-1：

④计算k 时刻的量测误差协方差阵Pzz,k|k-1和预测互相关协方差阵Pxz,k|k-1：

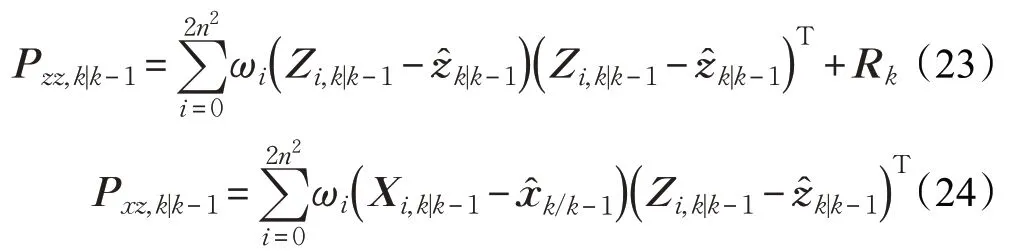
（4）滤波更新过程

计算k 时刻的滤波增益矩阵Kk、滤波状态值x̂k|k和协方差阵Pk|k：

3.3 统计线性回归的MCC方法

MCC方法的核心是使得定义的代价函数取得最大值。将MCC应用于HCKF，改变量测更新的方式，得到一种基于MCC 的鲁棒HCKF 算法。首先，定义k 时刻的状态预测误差为：

式中xk为k 时刻的状态真值，为k 时刻的一步预测值。根据式（6）可知组合导航系统的量测方程为线性，由文献[21]，此时式（22）～（24）可以表示为：

由以上三式，可以构造线性回归方程：

定义：

那么式（32）可以改写为：

定义代价函数：

式（38）可以等价表示为式（10）所示的MCC形式：

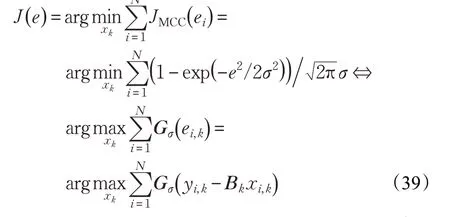
其中，N=n+m，ei,k为残差向量ei,k=yi,k-Bkxi,k的第i个分量。

通过对代价函数求取偏导数得到其最大值，对其求偏导得到：

记φk( ei)=ei,k⋅Gσ( ei,k)，上式可以改写为：

定义权函数Ck=φk(ei/ei)，式（41）可以进一步写为：

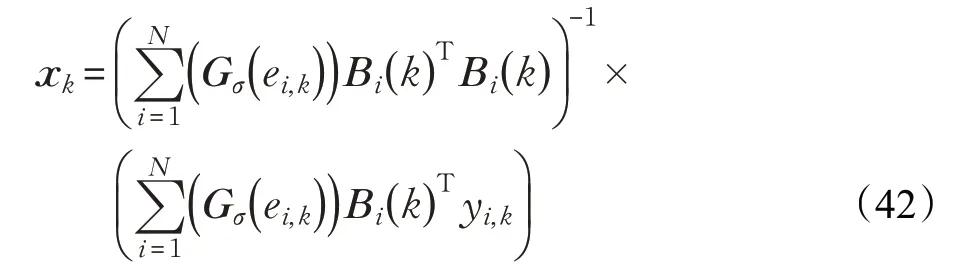
上式可以写成关于状态变量xk的迭代方程：

相较于梯度下降法，不动点迭代法无需选取迭代步长并且可以快速收敛到最优解附近，对上式采用不动点迭代算法进行求解得到：

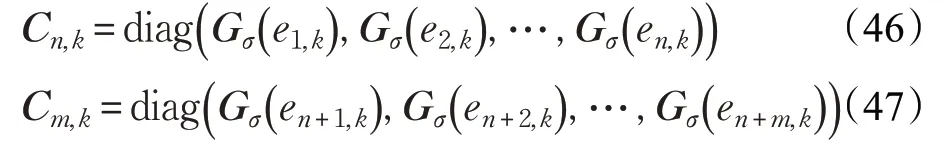
迭代结束后求得的方差为：

式（43）可以进一步表示为：

其中：

3.4 基于MCC的高阶容积卡尔曼滤波算法

将上述的MMC 方法和高阶容积卡尔曼滤波相结合，使得HCKF中的量测更新过程转化为求解线性回归方程的问题，得到新的鲁棒滤波算法，算法具体流程总结如下。

（1）初始化

（2）时间更新

MCC-HCKF的时间更新过程与3.2节中传统HCKF的时间更新过程一致，利用式（11）～（19）和容积点及其权重（14）、（18）得到k 时刻的一步状态预测xk|k-1和协方差Pk|k-1，然后采用Cholesky分解得到矩阵Sk。

（3）量测更新

①根据式（29）计算k 时刻的量测预测值ẑk|k-1，通过式（32）构造线性回归方程。

②将线性回归方程改写为式（37）的形式，令迭代次数t=1，同时设置初始迭代值为：

③代价函数取得最大值时，根据式（46）、（47）、（50）～（52）得到k 时刻的第t 次迭代状态为：

⑤最后，根据式（48）求得k 时刻的状态误差协方差阵Pk|k。

由上述算法流程可以看到，基于MCC 的鲁棒HCKF 的时间更新过程仍然采用了滤波精度高达五阶的高阶容积准则，这延续了HCKF 高精度的优点。MCC-HCKF和传统HCKF的区别在于前者建立了统计线性回归模型对传统量测更新过程进行了重构，并通过MCC 准则计算得到当前状态的估计值，相比于传统HCKF 更好地克服了非高斯噪声的影响，所以MCCHCKF 是一种兼具HCKF 高精度特点和MCC 方法鲁棒性的滤波算法。值得说明的是，当核宽σ →∞时，此时MCC-HCKF变为传统的HCKF，具体证明如下。

将上式代入式（45）可得：

显然此时MCC-HCKF和HCKF是等价的。

3.5 算法鲁棒性分析

文献[7-9]给出了基于Huber 鲁棒滤波算法的代价函数J( e )和权函数ψ( e )，由式（39）、（41）可知基于MCC的代价函数J( e )和权函数ψ( e )，具体表达式如表1和图2所示。

表1 代价函数与权函数

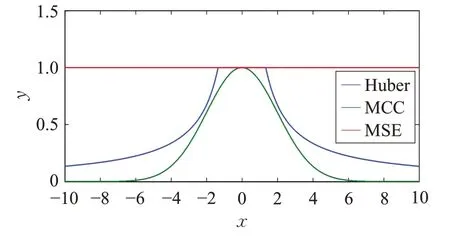
图2 权函数示意图

由图2 可以看到，传统滤波算法的权函数ψMSE( e)为常值，基于Huber 的权函数ψHuber( e )是由二段权函数构成，基于MCC 的权函数ψMCC( e )是由指数函数构成。由于ψMSE( e )=1，当出现量测异常时，传统算法无法减弱异常干扰，所以会影响算法的滤波精度和鲁棒性。当|e |＞α 时，ψHuber( e )会随着e 的增加逐渐减小以达到减小量测异常干扰的目的，然而ψMCC( e )会随着e 的增加呈现指数形式的衰减，相比于ψHuber( e )可以迅速减小到0附近，具有更快的衰减过程，所以可以有效抑制量测异常的影响，因此算法具有更强的鲁棒性。

4 仿真实验与分析

设置飞行器的初始位置为东经108°，北纬34°，高度300 m，载体初始速度大小为10 m/s，方向正北，载体经过加速、匀速、横滚、右盘旋、左盘旋、爬升、下降、减速等机动组成，具体机动如表2 所示；飞行轨迹如图3 所示，红色箭头表示飞机的起始位置。

SINS 的初始位置误差为10 m，初始速度误差为0.5 m/s，东向、北向初始失准角为1°，天向失准角为1°。GPS的水平位置误差均方根为10 m，高度误差均方根为3 m，速度误差均方根为0.1 m/s。SINS 的解算周期为0.01 s，GPS信号采样周期为0.1 s，飞行时间600 s。初始方差阵P(0)、系统噪声阵Qk设置为：

为了验证本文提出的鲁棒滤波算法的有效性，设置两种情况对提出的算法进行实验，结果及分析如下。

表2 飞行器轨迹仿真

图3 飞行轨迹图

定义k 时刻的位置RMSE为：

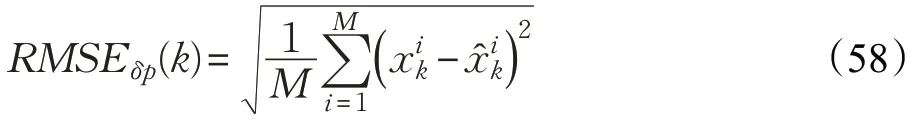
定义k 时刻的位置ARMSE为：

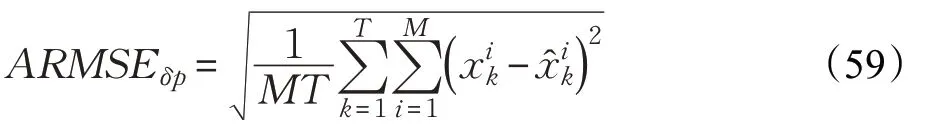
实验1 量测信息为高斯分布。

在飞行过程中，假设GPS 的量测信息正常，此时量测噪声满足如下形式的高斯分布：

图4 高斯噪声条件下的位置RMSE

表3 高斯噪声条件下的位置ARMSE m

结合图4和表3的实验结果可以看出，100 s后组合导航系统滤波器收敛，此时HCKF 的定位误差小于CKF，由此可知采用高阶容积规则的HCKF表现优于采用三阶容积规则的CKF。MCC-HCKF表现和HCKF大致相同，但是定位精度略低于HCKF这是因为在高斯噪声环境下，HCKF 是基于最小均方差的滤波器，当噪声服从高斯分布时其表现自然最优，此时MCC-HCKF 的鲁棒性是以牺牲一定的滤波精度来换取的。

实验2 量测信息为受污染的高斯混合分布。

在飞行过程中，假设GPS的量测信息为受污染的高斯白噪声，此时量测信息服从高斯混合分布，而且方差是原高斯分布的10倍。式（61）给出了受污染的高斯白噪声的概率分布表达式，式中ε 为混合百分比，其取值范围为0～1，显然当ε=0 时，噪声服从理想的高斯分布，本文取ε=0.2，同时增加文献[14]中的H-HCKF作为对比算法，参数α=1.345。

从图5 可以看出，当量测噪声不再满足高斯分布时，传统的HCKF 的滤波精度均下降，说明算法无法有效抑制非高斯噪声对系统的影响，而MCC-HCKF 滤波此时表现出了良好的滤波性能，精度高于HCKF。这是因为MCC-HCKF滤波算法在进行与HCKF相同的时间更新后，在量测更新过程中通过数值迭代求解的方法，进行了一次基于MCC 的线性回归估计，这一过程可以减弱观测噪声与假设分布之间的偏差对滤波器的影响，但同时也会增加一定的计算量。随着核宽σ 的减小，滤波器的鲁棒性增强，精度也随之提高。随着核宽σ 增大，鲁棒性下降，滤波器的表现越接近HCKF，这与上文的理论证明是一致的。对比图中H-HCKF和MCC-HCKF的估计曲线，可以发现H-HCKF 也具有较高的滤波精度，高于MCC-HCKF(σ=4)，低于MCC-HCKF(σ=3)，说明此时MCC-HCKF(σ=3)表现略优于H-HCKF。

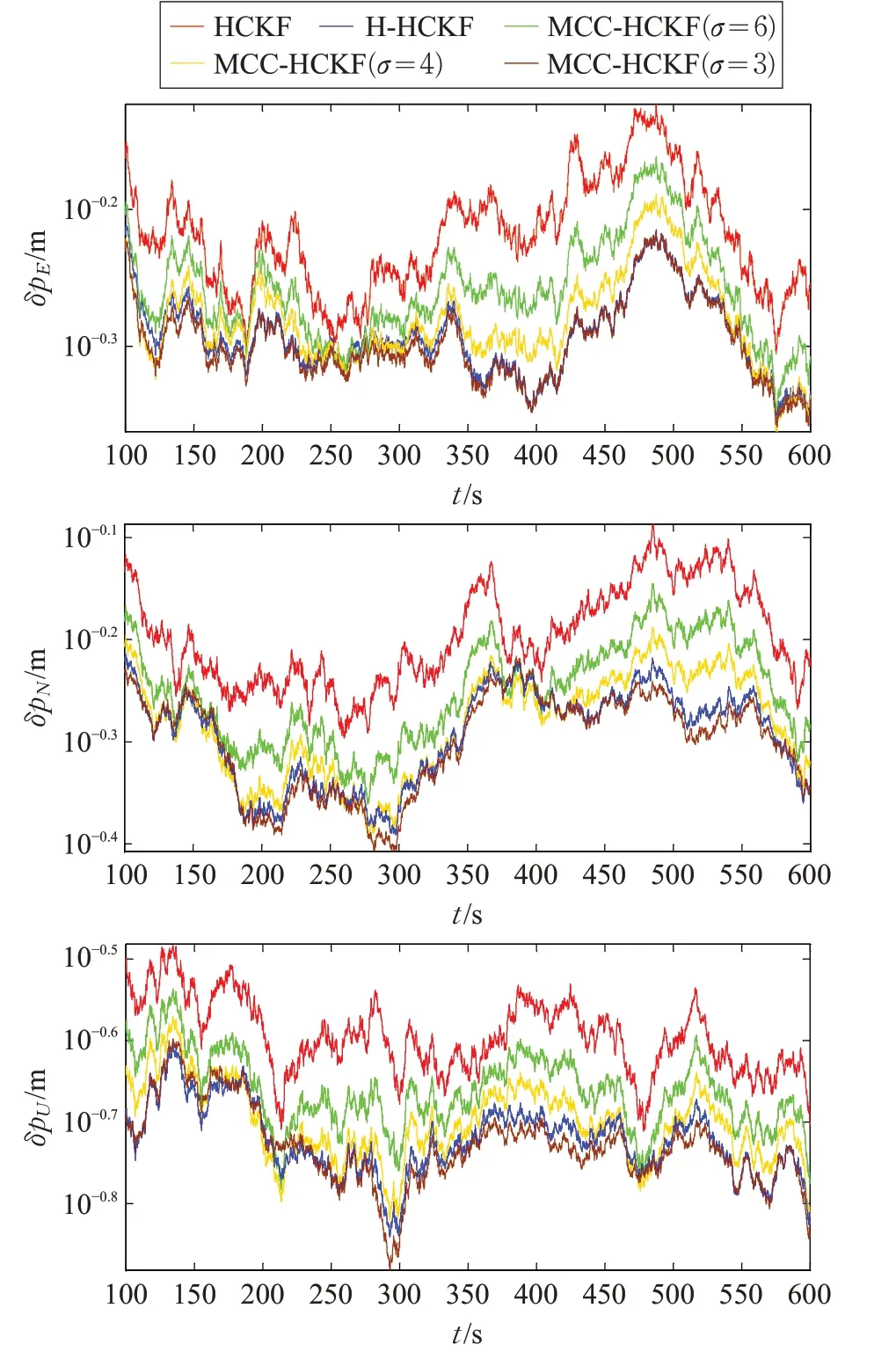
图5 非高斯噪声条件下的位置RMSE

为了比较上述五种算法的计算时间，仿真软件采用Matlab2014a，仿真处理器为Intel Inside Core i5处理器，将HCKF、H-HCKF、MCC-HCKF(σ=6)、MCC-HCKF(σ=4)、MCC-HCKF(σ=3)五种算法的单次蒙特卡洛仿真实验所消耗的运行时间进行统计，结果如表4所示。

表4 五种滤波算法蒙特卡洛实验时间统计

为了进一步分析核宽σ 对组合导航定位精度的影响，图6为不同σ 条件下的位置ARMSE。由图可知，在σ=2.5 附近经度、纬度和高度的ARMSE达到最小，大于或者小于这个值都会增大定位误差，需要指出当σ →0此时滤波器将会出现数值稳定性问题，滤波精度急剧下降，说明选取合适的σ 对组合导航的定位精度有着较大的影响，σ=2.5 时系统受到非高斯噪声的影响更小。需要说明的是，当组合导航系统工作环境恶劣或者仪器发生故障时，量测噪声的分布与高斯分布会存在较大的偏差，根据3.4节中的证明过程，当σ →∞，MCC-HCKF是和传统HCKF等价的，所以此时应需要尽可能选取较小的核宽σ 来抑制非高斯噪声的影响。值得说明的是，通过上述实验结果可以发现非高斯噪声主要通过量测值来影响组合导航系统的工作性能，所以下一步可以研究核宽σ 与残差间的关系，进而达到自适应调整核宽的目的，使得算法具有更强的自适应性和实用性。

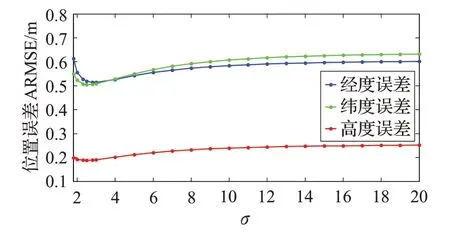
图6 不同σ 下的位置ARMSE

5 结论

本文以SINS/GPS 组合导航为研究背景，给出了组合导航系统的非线性误差模型以及滤波器的状态方程和量测方程，针对组合导航量测噪声不服从高斯分布的问题，将高阶容积准则和统计线性回归模型结合，提出了一种新的基于MCC方法的鲁棒高阶容积卡尔曼滤波算法，并进行了仿真实验。仿真结果表明，在选取适当核宽的条件下，该方法可以有效解决系统非线性和量测噪声非高斯的问题，能够提高组合导航的定位精度。