结合视点变换的三维地形无缝绘制算法

杨 燕，王慧青，焦 越

东南大学 仪器科学与工程学院，南京210096

1 引言

随着测绘领域采集技术和存储技术的发展，获得的三维地形数据规模越来越大。当前，国内外主要通过多分辨率技术[1-2]对地形数据进行精简，实现海量三维地形渲染。但由于不同分辨率网格在边界处存在层次差异，渲染过程中易出现裂缝，裂缝问题是多分辨率地形中必须解决的一个问题。

对于裂缝消除，传统方法主要有裙带算法和调整网格边界顶点。裙带算法[3-4]是为不同层级的地形网格在其边缘处添加一个包围体，当网格层次不一致时，由于该包围体的存在，在视觉上可挡住裂缝。但裙带算法为消除裂缝增加了较多的三角网格，且高度难以控制。调整网格边界顶点[5-6]分为分裂较高层次网格和合并较低层次网格，该方法应用范围最广，但当相邻网格层次差大于1时算法会变复杂。除以上两种算法外，文献[7]提出基于渐进网格的聚类层次模型，可有效消除裂缝。文献[8]提出在相邻地形交界处保证重合顶点获取的高程值相同来实现无缝连接。文献[9]提出通过构造曲线拟合函数控制不同层次网格顶点的布局从而消除因LOD产生的裂缝。文献[10]提出根据线性差值算法修正四叉树中互为邻居关系的瓦片高程以消除地形裂缝。但这些方法都或多或少需要增加最终绘制的网格数量，且无法解决地形在相邻层级间分辨率的突变问题。

鉴于以上分析，本文提出一种改进的基于视点的裂缝消除算法，通过CPU-GPU协同工作，根据精度要求完成数据的分层分块，利用纹理映射技术生成LOD 精细模型，并根据视点动态调整顶点位置达到消除T型裂缝的目的。

2 地形数据预处理

2.1 CPU-GPU结合的模型构建方式

本文提出一种CPU-GPU[11-12]协同构网的方式，渲染流程如图1 所示。整体框架包括CPU 模块和GPU 模块。首先将地形高度图作为纹理数据，以二维数组的格式保存至GPU 中。在CPU 中，根据精度要求建立粗糙LOD模型[13-14]，每一个网格中只保存四个边界顶点的坐标及其网格尺寸。然后通过视锥裁剪将符合要求的子节点队列传入GPU中。

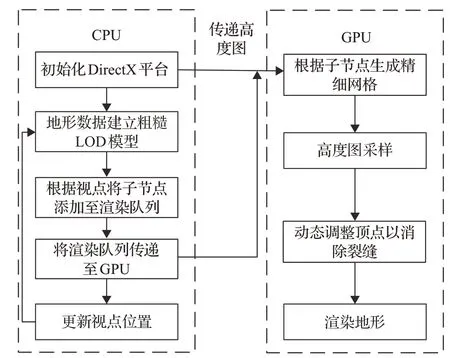
图1 CPU-GPU结合的渲染方式

在GPU中，利用高速处理器并行构建LOD模型，生成精细网格，再通过纹理映射技术对高度图进行顶点采样，获取高程数据并映射到网格顶点上，实现从二维顶点到三维顶点的转变。然后根据视点动态地调整顶点位置以实现裂缝消除，完成地形渲染。

这种利用CPU-GPU 结合生成多分辨率模型的方式，将构建精细网格的工作交给GPU，CPU中只需根据视点对子节点进行视锥裁剪，充分利用GPU 并行处理的能力，减轻CPU的负载。同时，GPU中有成百上千可高速并行工作的处理器核心，地形的网格构建和渲染工作交由GPU 并行处理，比在串行的CPU 上运行速率更快，可以节省整个系统中数据的处理时间。

2.2 地形数据组织及包围盒构建

本文选择DEM 数据作为高度数据，以规则格网方式组织地形数据。采用自顶向下的规则建立多分辨率四叉树模型，模型中每块地形边长都需满足(2n+1)×(2n+1)，以左上角为起点，对于右侧和下方不满足条件的地形块，以无效数据填充。图2（a）所示即为四叉树LOD 模型的生成过程，根据每个节点的精度是否达到系统的阈值来判断当前节点是否需要继续剖分。如果剖分，则上一层的子节点是下一层的父节点，每个非叶子节点包含四个子节点。为了减少在CPU中计算每个顶点的具体坐标值以及构网的过程，将每个地形块的具体三角化过程放入GPU中。每个子节点只保存四个特征顶点的坐标信息以及在世界坐标系中的尺寸，地形渲染时这些数据会一同传入GPU。如图2（a）所示，1、2、3、4即为地形子节点A的四个特征顶点。

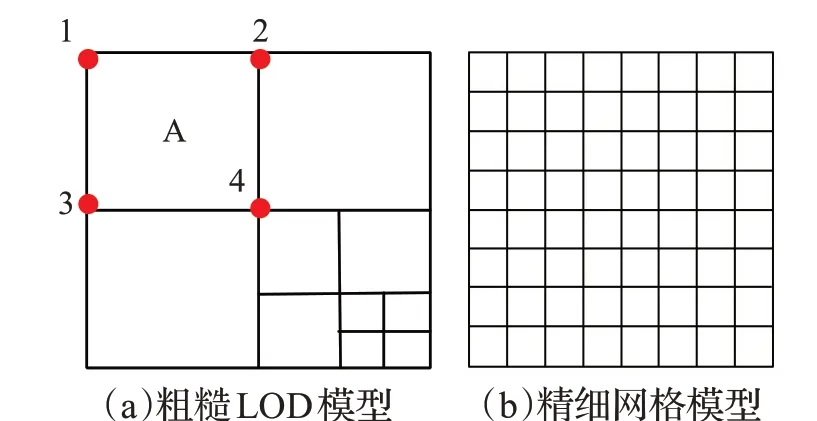
图2 地形数据分块

GPU 中调用的渲染函数是限制本文算法性能的关键，每个子节点都必须调用一次渲染函数。如图2 所示，输入数据为图2（a）中的某个子节点，在GPU中该节点被继续分割成图2（b）所示的(2n+1)×(2n+1)顶点（图2（b）中n 取为3，子节点分割为9×9 顶点），这些顶点是绘制地形的最小单元。每个子节点中顶点个数达到65×65时，若继续细分顶点，最终渲染的地形差异不大，但会产生数据冗余，如果少于9×9，将不足以表达地形的细节，因此地形子节点的个数需控制在9×9 至65×65之间，即n 需控制在3 至6 范围内。假设n 取6，叶子节点最高处于m 层，整个地形的最高分辨率为(2m+6+1)×(2m+6+1)，考虑到本文的DEM 数据，叶子节点处于第8级时，地形的最高分辨率达到(214+1)×(214+1)，此时顶点的精度在五米左右，继续对节点进行剖分，精度提升不大，但性能将有所降低。因此本文m 值最高取8，此刻渲染的地形精度已满足要求。

在GPU中根据每个顶点的序列号获取其三维坐标的方式如公式（1）所示。假设某个顶点对应的序列号为(i,j)，根据此序列号获得其在x 轴和z 轴方向的实际坐标值，进而获取其高程值：

其中，Xmin、Zmin为当前地形块四个特征顶点中左上角的顶点坐标，heightmap 为获取顶点高度的函数，l 为当前的顶点间隔。

在实时渲染时为了利用视锥体裁剪部分节点，可对地形块构造包围盒[15]。包围盒的四个顶点取节点的四个特征顶点，坐标分别为(Xmin,Zmin)、(Xmin,Zmax)、(Xmax,Zmin)、(Xmax,Zmax)。包围盒的高度Y 取该子节点区域内所有采样点的最大高程值，为减少数据的访问量，可用四个边界顶点以及对角线交点中的最大值代替。

根据三个方向的坐标值构造包围盒，该包围盒对角线的长度为：

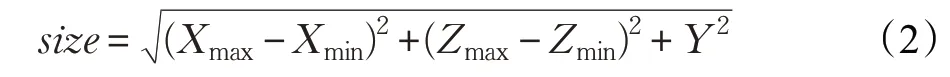
3 基于视点和GPU的LOD地形无缝绘制

在海量地形实时渲染时，由于相邻网格细节层次不一致，导致高层次网格与层次较低的网格边线不一致，在相邻瓦片间产生空隙，致使在虚拟空间中漫游时出现裂缝的现象。如图3 所示即为裂缝产生的示意图。为了避免裂缝问题，保证画面渲染的连贯性，消除裂缝必不可少。

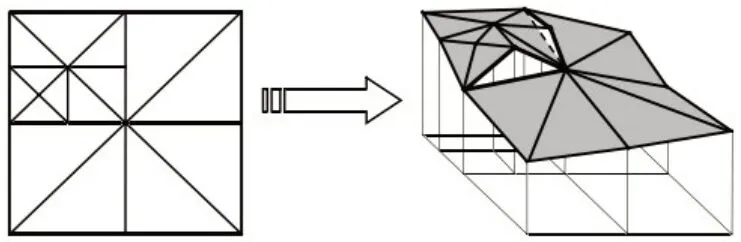
图3 裂缝产生示意图

对裂缝进一步分析发现，在高层级节点中x 和z 方向序列号皆为偶数的顶点在低层级中被保存下来，这些顶点对裂缝无影响。但是在x 或z 方向序列号中出现奇数的顶点在低层级中不再存在，在相邻地块交界处，也是因为这些奇数序列的顶点才导致裂缝的产生。因此本文提出只要调整序列号为奇数的顶点的位置，使其在网格边界处与序列号为偶数的顶点重合，即可消除裂缝。

相对于传统的垂直裙带法、增边法（删边法）等方法，本文提出了一种改进的基于视点的动态调整顶点法处理裂缝，该算法在生成网格过程中直接处理网格的裂缝，无需添加多余的网格，也不需要限制相邻层级层次差≤1。

3.1 基于视点和包围盒的视锥裁剪

为了提高系统的性能，减少每次渲染的三角网数量，在绘制地形之前需要先剔除一部分网格。本文采用视锥体方式[16]，在向GPU 传递子节点时，只传递在视锥体范围内的节点，其余节点一律舍弃。视锥体如图4所示，它有六个面，本文假设每个面的法向量都指向视锥体内部，则可以确定六个裁剪方程：

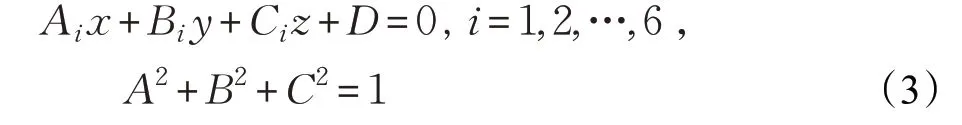
对于某个顶点P，其坐标为(xp,yp,zp) ，该顶点到其中某个面的距离为：

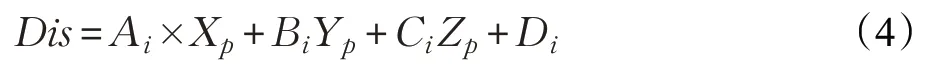
此时计算出的距离Dis 是一个带符号的变量，表示在平面的不同方向，若符号为正，表明点在平面正方向，反之，点在平面反方向。若顶点p 到六个面的距离中只要有一个是小于0，可判断该顶点此时在视锥体外部，否则位于视锥体内部。

基于以上方法，判断一个地形块节点是否在视锥体内部，即判断其包围盒与视锥体的位置关系。首先可确定包围盒对角线的距离为size，根据公式（4）计算包围盒中心点到视锥体六个面的距离，若包围盒中心点到某个裁剪面的距离Dis 小于-size/2，可判断此时整个包围盒都不在视锥体中，属于不可见地块。

基于以上分析，视锥体与包围盒的关系可以分为以下三种：

（1）地形块节点对应的包围盒完全在视锥体内部，该节点属于可见节点，可根据视点到节点中心点的距离判断是否需要继续剖分，如图4中的包围盒A所示。

（2）地形块节点与当前视锥体存在交叉，认为该地形块部分存在于视锥体内部，将根据距离因素判断是否需要继续剖分，若剖分，将依次判断四个子节点是否在视锥体内部；否则该节点将被直接存入渲染队列中，等待传入GPU，如图4中的包围盒B所示。

（3）节点完全位于视锥体外部，舍弃该节点，如图4中的包围盒C所示。

图4 视锥体构造

3.2 基于视点的LOD无缝绘制

在渲染地形节点前，为了明确最终哪些节点将被传入GPU，需提前计算每个LOD 层级的节点覆盖的最远距离。由于本文采用的四叉树结构，因此相邻层级的节点之间分辨率差异为四倍，在线性方向上，分辨率差异为两倍[17]。基于本文自顶向下创建网格模型的过程，在生成网格的过程中创建一个可视距离数组m_visibilitys。根据叶子节点最高层级为7 以及相邻网格间线性分辨率差异为2倍，可计算出整个地形的最远距离fardist ，根据该距离可计算出每个层级之间距离的递增因子sec：

根据该递增因子可获得每一层级最终的可视距离：

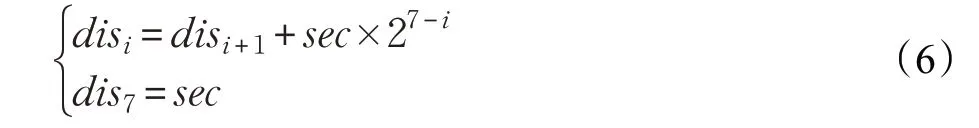
地形渲染时，从根节点开始进行判断，若该节点至视点的最小距离大于当前层级的可视距离，则认为该节点超出当前视点的可视距离，该节点不予绘制。若节点至视点的最小距离在当前层级和下一层级的可视距离范围内，且节点在视锥体内，则将该节点添加至渲染队列。若节点至视点的距离小于下一层级的可视距离，将对该节点进行剖分，并递归判断其四个子节点。最终，所有需要被渲染的节点都保存在渲染列表中。

为了消除裂缝，在获取每一层级叶子节点的可视距离时，同时会获取该层级的调整范围，渲染时每个顶点都需进行判断，若顶点至视点的距离处于当前层级的调整范围内，则该顶点将会相对原来的位置发生一定的偏移。每一层级的调整范围为其中：

其中，mratio 为调节参数，根据该参数可以调节顶点从何处开始发生调整，假设该值设置为0.6，此刻变形区域占每个地形块总体的比例将大于40%。

地形子节点被传入GPU 中后生成地形模型，获得每个顶点的实际坐标，根据每个顶点的实际坐标会判断该顶点的位置是否调整，调整公式如下：

其中，x、z 为局部坐标转换为世界坐标后的对应坐标值，dis 是当前顶点到视点的距离，clamp 函数保证返回值始终处于0-1 之间，frac 函数返回当前数值的小数部分，scale 为当前地形子节点的尺寸大小，griddim 为当前子节点将会在x、z 方向分割的顶点数，它是绘制地形的最小单元，morph 为当前节点的调整系数。从上述公式可以看出，顶点分为两种情形：

（1）某个顶点到视点的距离小于当前可变距离的开始位置，即mstart ，此刻clamp 函数直接返回1，因此参数morph=0，此时顶点无需调节。

本文算法对顶点位置的调整过程如图5所示。图5（a）为高层级地形的一部分，离视点较近，顶点未偏移，图5（d）为低层级的地形，位置紧挨高层级地形块，图5（b）、（c）和图（a）处于同一层级，但由于图5（b）、（c）中的顶点离视点越来越远，因此其中序列号为1 和3 的顶点的位置相对于其原始位置发生了一定的调整，图5（c）离视点的距离比图5（b）更远，顶点相对于其原始位置偏移的更多。在与图5（d）的交界处，根据公式（8）和（9）可知，此时序列号为奇数的顶点将会与其相邻的顶点重合，因此在边界处的顶点都和图5（d）重合，消除裂缝。实验部分给出了最终的绘制效果，可以看出，最终绘制的地形不存在裂缝，且网格保持连续。

图5 裂缝消除示意图

通过上述可知，在相邻层级的地形交界处，高层级地形中序列号为奇数的顶点相对原来的坐标已被调整，和序列号为偶数的顶点相重合。在边界处，高层级地形块的顶点和低层级顶点重合，裂缝被消除。该方法不仅能在生成网格的过程中直接消除裂缝，同时层级之间的过渡较为平缓，不会产生突变的现象。

4 实验结果

为了验证该算法的可行性，本文进行了相关实验。实验的硬件平台CPU为Intel®Core™i5-3470 3.6 GHz，内存为8 GB，显卡型号为NVIDIA GeForce GT 630，显存为1 GB，开发工具为Visual Studio 2010，DirectX 9.0版本，该实验渲染时的屏幕窗口大小为1 024×768。测试数据为来自云南省某县级区域的DEM 数据，该地区地形主要为山区，区域范围为90 km×40 km。四叉树模型自顶向下分为八层。设计以下三个实验来验证本文中所描述的算法。

实验1 不同调节参数mratio 控制下的地形实时渲染效果。

图6（a）为mratio=1 时的地形，根据公式（10）可知，参数为1 时mstarti=mendi，morph=0，顶点位置未发生调整，渲染的地形呈现原始状态，因此存在裂缝，图6（b）是裂缝的放大示意图。图6（c）为mratio=0.8 时渲染的地形，从图中可看出有部分网格发生了调整，且每一次调整的幅度较大，但由于此刻mratio=0.8，因此只有靠近边界线的一部分顶点位置被调整，大部分顶点维持不变。图6（d）为mratio=0.6 时渲染的地形，此刻位置发生偏移的顶点数量更多，只有部分顶点还维持不变，顶点间每次调整的幅度与0.8时相比明显小了很多。

图6 不同调节参数渲染的网格

以上实验结果表明，本文的算法可以有效解决裂缝问题，此外当mratio 位于0.8至0.9之间时，既能保证大部分网格保持原样，也能保证部分顶点发生动态偏移，在边界处可消除裂缝。因此，mratio 取0.8 至0.9 范围内的数值较为合适。

实验2 在GPU中绘制每个子节点时选取四种网格尺寸进行对比。

表1为不同网格尺寸下渲染的三角形个数、GPU占用率以及帧速率对比。从表1 中可以看出当网格尺寸达到65×65 时，每一帧渲染的三角形个数接近百万，但整体系统未出现卡顿现象。观察GPU 的负载，虽然渲染的三角形个数不断增加，但GPU的负载变化不大，始终维持在20%以内，且CPU的负载维持在10%左右。测试结果说明本文提出的CPU-GPU协同工作的渲染方式可以充分利用GPU的超高计算能力，降低CPU负载。

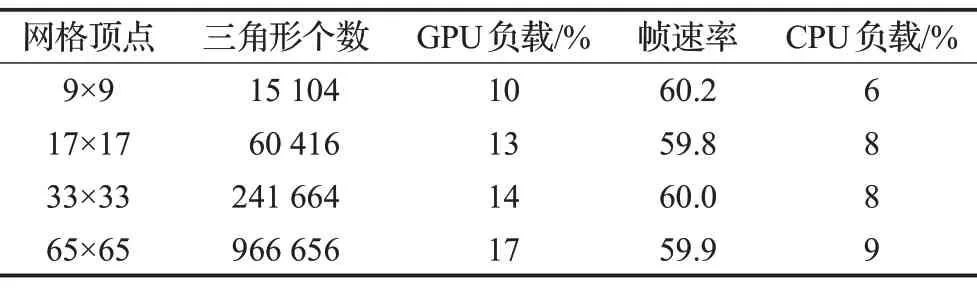
表1 不同网格尺寸的渲染结果对比

观察帧速率可看出，帧速率始终维持在60帧左右，并未随着三角网个数的增长而降低，完全满足流畅性的需求，达到了实时渲染与数据调度的平衡。

实验3 在相同的硬件环境下，将本文的裂缝消除算法与传统的边删除裂缝消除技术进行了比较，采用的数据为根据柏林噪声生成的地形数据。

图7（a）为本文算法渲染的地形，图7（b）为传统LOD 技术渲染的地形，图7（c）和图7（d）为两种方法裂缝处理的细节；表2为本文算法与边删除技术的一些参数对比。

图7 本文算法与边删除技术的对比

表2 本文算法与边删除算法的技术对比

实验结果表明，边删除技术对层级之间的要求较高，需控制层次差不超过1，对于不符合要求的地形块需不断进行剖分，产生数据冗余，且该算法中网格模型的生成等一系列工作都是在CPU 中完成，因此绘制阶段CPU 负载在45%左右。本文算法对相邻地块层级无限制，在绘制阶段对于CPU 占有率低于10%，几乎无占用。此外两种算法的帧速率都稳定在60 f/s 左右，但本文平均绘制的三角网个数大于边删除法，说明本文的算法可以较好地保持地形的基本地貌特征。

5 结束语

本文在分析常规方式消除LOD模型中的裂缝的基础上，提出一种基于视点的裂缝实时消除算法。该方法在数据预处理阶段根据精度要求生成粗糙的LOD 模型，并构造相应的包围盒；然后利用视锥裁剪和纹理映射技术生成精细的网格模型；最后根据视点动态调整顶点位置以实现T 型裂缝的消除。此外，本文采用CPUGPU协同工作的方式，将大量工作从CPU移植到GPU，提升了整个系统性能。实验结果表明，本文提出的方法不需任何额外的补丁，地形的层次差不受限制，即可在生成地形的过程中将裂缝删除，每次渲染的三角网个数可达到百万级别，适用于海量地形。