基于数据深度的过程工业故障检测方法

车建国，赵 赛

南开大学 商学院，天津300071

1 引言

过程工业也称流程工业，是指加工制造流程性物质产品的制造业，化工、炼油、冶金、轻工、建材、制药等行业均属于过程工业。随着现代过程工业的发展，产品多以大批量的形式生产制造，由于其生产过程往往具有投入成本高、事故后果严重等特点，一旦某个过程发生了故障，有可能会引起整个生产的故障发生或者导致生产停止，严重的甚至可能危及生命安全、造成巨大损失。因此对过程工业的生产过程进行监控有着十分重要的意义，可以有效地减少无效投入、避免事故发生等。

过程工业的质量监控中最重要的就是故障检测，即根据系统的过程参数变量来提取能反映系统异常变化或故障特征的信息，进而判断当前运行的系统是否处于受控状态，若检测到故障发生则应当立即报警，以便管理人员采取相应的措施。目前常用的故障检测方法可以大致分为基于统计模型的方法、基于距离的方法、线性变换及非线性变换的方法。主元分析（PCA）作为一种多元统计分析方法，由于其易用性被广泛地用于多元过程工业的故障检测[1-2]，它利用多元投影的方法将多变量样本空间分解成由主元空间张成的较低维的投影子空间和一个相应的残差子空间，分别在这两个子空间进行投影，并计算相应的统计量进行过程监控。但主元分析只适用于处理多元数据的线性关系，对于非线性关系不能很好地进行特征提取，于是有学者提出核主元分析（KPCA），通过将输入数据映射到高维空间中来解决过程数据间的非线性关系[3-4]。此外，还有学者将小波去噪与核主元分析方法结合应用于故障检测[5]，但基于传统多元统计的方法大都要求输入数据的总体满足一定的分布形态，而现实中对过程工业变量的分布大多是未知的，这样使得检测结果的稳健性无法得到保证。近年来，许多机器学习的分类算法如人工神经网络、支持向量机[4，6]取得了积极的进展，这对于故障诊断领域的理论发展和实际应用具有良好的推动作用，但这些方法只强调输出结果（故障与否），忽略了过程工业样本点本身的位置、尺度等特征，难以解释各样本数据之间的关系如偏离正常运行状态的程度。

数据深度（统计深度）是用“深度”来度量某样本点相对总体的位置，越靠近中心的样本点深度值越大（越“深”），越偏离中心的样本点深度值越小（越“浅”）。作为近年来蓬勃发展的一种统计方法，数据深度本身用于解决多元数据的排序问题，其规范定义由左义君等给出，并介绍了统计深度函数应该具有的四个性质[7]。数据深度函数在统计推断时具有良好的仿射不变性和稳健性估计，当数据污染时仍然能得到很好的位置估计[8]。考虑深度值从中心向外单调递减的特性，有学者提出了根据深度值判断数据是否异常的检测模型，并通过实例证明了该检测方法的有效性[9]。由于数据深度具有良好的非参数稳健性，近年来越来越多地被应用于位置推断、回归分析、多元非参控制图和多元数据的判别与分类问题[10-12]。

考虑到相对于正常运行状态下的样本集，待测样本的深度值越小越有可能是故障样本，结合数据深度的非参数特性，构造深度值的秩统计量渐近分布，提出基于数据深度的故障检测方法，将数据深度技术应用于复杂过程工业的质量监控。通过对TE过程故障检测结果的分析，验证了该方法的有效性，为实际过程工业的故障检测提供了一定的决策参考。

2 基于数据深度的故障检测

目前学者提出的深度函数有很多，如马氏深度、空间深度、半空间深度、单纯形深度、投影深度等，而在这些深度函数中，空间深度和马氏深度由于计算复杂度较低且其复杂度不随数据维数的增大而增大，被广泛应用于监测和分类问题[12-14]。

马氏深度（Mahalanobis Depth，MD）：

其中x ∈Rn为待测样本，F 为总体的累积分布函数，μ,Σ 分别为总体的均值向量和协方差矩阵，在实际计算时可用样本的均值向量、协方差矩阵来代替。

空间深度（Spatial Depth，SD）：

其中x,y ∈Rn，F 为总体的累积分布函数，x ∈Rn为待测样本点，为欧几里得范数。当总体分布F 未知时，样本形式的空间深度如下：

其中X={ x1,x2,…,xl} 为l 个n 维样本，x ∈Rn为待测样本。

可以看出，不管马氏深度还是空间深度，某一样本点的深度值总是在[ ]0,1 之间，样本点从中心向外移动的过程中其深度值递减。对于马氏深度，在总体的均值向量μ 处取最大深度1；对于空间深度，在满足的点x(x ∈Rn)处取最大值1，点x 称为空间中位向量（由一维中位数推广而来）。当总体不满足对称分布时，中位向量要比均值向量更能代表总体中心的位置，具有更稳健的位置估计。

从空间深度的定义中可以看出，深度值的大小取决于从待测样本点x 到X 中每个样本点的累积方向向量的模，这在一定程度上只考虑了偏离的方向，而忽略了偏离的距离度量，尤其对于高维数据，可能无法代表真实数据的分布偏离特征，文献[9]以半月形数据和环形数据为例验证了这一情况。为了综合考虑待测样本点x 与总体X 中各样本点的距离差异（相似度差异），引入核方法，如最常用的高斯径向基核函数k(x,y)=考虑到：

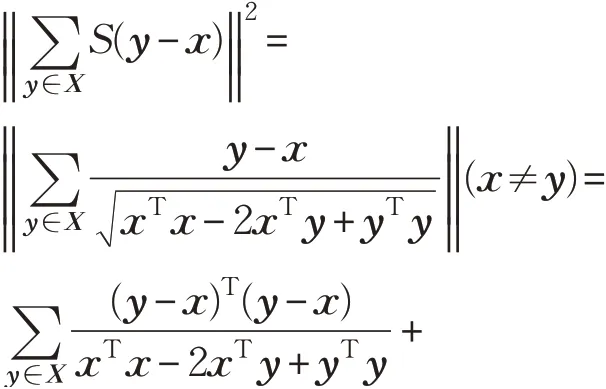
使用高斯核函数k(⋅)代替内积，得到核化的样本形式的空间深度（Kernelized Spatial Depth，KSD）：

前文提到，由于数据深度反映了样本点与中心的偏离程度，待测样本的深度值越小说明其离中心越远，因此深度值越小的待测样本越有可能是故障样本，而且数据深度本身具有很好的非参数特性，因此可以利用非参数秩统计量的有关性质来判断样本点是否异常。

假设y1,y2,…,yn为n 个来自总体X 的验证集样本，将这n 个验证集样本代入式1（式4），分别得到其相对于训练集X 的马氏深度值（核空间深度值）Di。将D1,D2,…,Dn这n 个验证集样本的深度值从小到大进行排序即当时定义Ri=r,即得到各样本点对应的秩。

记R=(R1,R2,…,Rn)，很容易得到R 的所有取值有n!种可能，即

故秩统计量R=(R1,R2,…,Rn)服从离散均匀分布，且R=(R1,R2,…,Rn)的边缘分布也是均匀分布。特别地，一维均匀分布有：

二维均匀分布有：

从而可以得到：

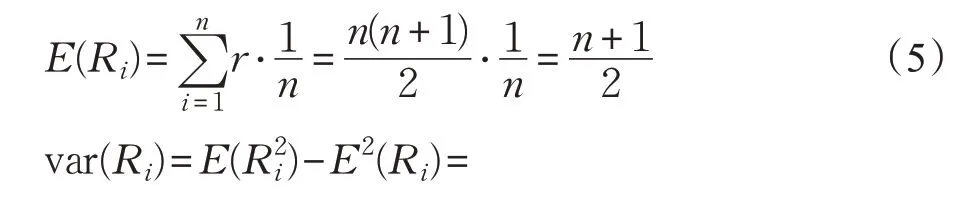
根据线性秩统计量的渐近正态性[15]，当样本量足够大时，构造

给定显著性水平α 后，可以用该近似公式得到拒绝域的临界值Rα，对应可得到深度值的阈值MDα和KSDα。确定相应的阈值后，若待测样本的深度值小于该阈值，则将该样本对应的状态视为故障状态，否则为正常状态。

使用核空间深度（马氏深度）进行过程工业故障检测的步骤如下：

（1）获得正常运行过程下的训练集数据X (X ∈Rl×n)，对X 进行列标准化处理，即1,2,…,n，E(Xi)和std(Xi)分别为列变量Xi的均值和标准差。

（2）根据训练集数据建立深度函数模型（对于核空间深度需要确定核参数σ）。

（3）获得正常运行过程下的验证集数据Y(Y ∈Rl'×n)，代入（2）中模型计算深度值，根据式（7）来确定相应深度函数的阈值。

（4）对待测样本按（1）中求得的E(Xi)和std(Xi)进行标准化处理。

（5）对经过标准化处理的待测样本，根据（2）中模型计算其深度值，与对应的阈值相比较，若小于阈值则视为故障状态，否则视为正常状态。

这样就建立了基于数据深度的故障检测模型，根据此模型可以用来检测新的待测过程样本是否正常，即判断生产过程是否处于受控状态，以便管理人员采取相应的措施。接下来以TE 过程为例，来验证该检测方法的有效性。

3 TE过程介绍

TE 过程（Tenessee-Eastman Process）是由美国伊士曼化学公司控制小组的Downs 和Vogel 提出并创建的，目的是为评价过程控制和监控方法提供一个现实的工业过程。TE 过程具有一般过程工业的典型特征，其变量众多、强耦合、非线性且具有不确定性，因而成为国际公认的监测和控制领域最常用的检测算法性能的过程之一，也一直被认为是一个富有挑战性的问题，很多学者使用TE过程来检验算法的有效性[16]。

TE 过程主要包括5 个单元：反应器、冷凝器、压缩器、分离器和汽提塔，生产过程包含8种成分，生产过程包含41个测量变量（XMEAS（1）～XMEAS（22）为测量，采样间隔为3 min，XMEAS（23）～XMEAS（41）为生产过程成分组分，所有过程测量均包含高斯噪声）和12个控制变量（XMV（1）～XMV（12）），共52 个观测变量（除搅拌器速度）。

仿真包括21个预设的故障类型，故障0表示正常工况，故障1～16及故障21已知，其中故障1～7与过程变量的阶跃变化有关，如冷水入口温度或者进料成分的变化；故障8～12 与一些过程变量的可变性增大有关，故障13 是反应动力学中的缓慢漂移，故障14、15 和21 与粘滞阀有关，故障16～20未知。

正常状况的训练集数据是在25 h 仿真运行下采集的，共500 个；正常状况的测试集数据是在48 h 仿真运行下采集的，共960个。故障类型的训练集数据也是在25 h仿真运行下采集，但故障从1 h引入，观测数据是在引入故障后才开始采集的，即只有480 个观测值；故障类型的测试集数据也是在48 h 仿真运行下采集的，共960 个，但故障在第8 h 引入，即前160 个观测值是正常工况的样本数据。

4 结果对比分析

对于每种故障类别，先根据500个正常训练集样本建立模型，使用600个正常验证集样本来确定阈值t，然后进行测试集样本的故障检测，即分别计算对应故障类别的16 个小时运行状态下的测试集样本的深度值，其中故障从8 h引入，即第1～160个样本为正常运行状态，第161～320个样本为故障状态，得到各自的马氏深度值MD、核空间深度值KSD。在计算核空间深度时使用高斯径向基核函数，其中经多次实验取σ=25。取显著性水平α=0.05，根据500个训练集样本和600 个验证集样本，分别得到核空间深度阈值tKSD=0.192 0，马氏深度阈值tMD=0.011 1。以故障1为例，图1和图2分别为320个故障1测试集样本的核空间深度值与马氏深度值。

可以看出，对于故障1，核空间深度将156个故障样本检测出来，检测效率97.5%，仅将1个正常样本误判为故障，误报警率0.63%；马氏深度将159个故障样本检测出来，检测效率99.38%，同时将4 个正常样本误判为故障，误报警率2.5%。

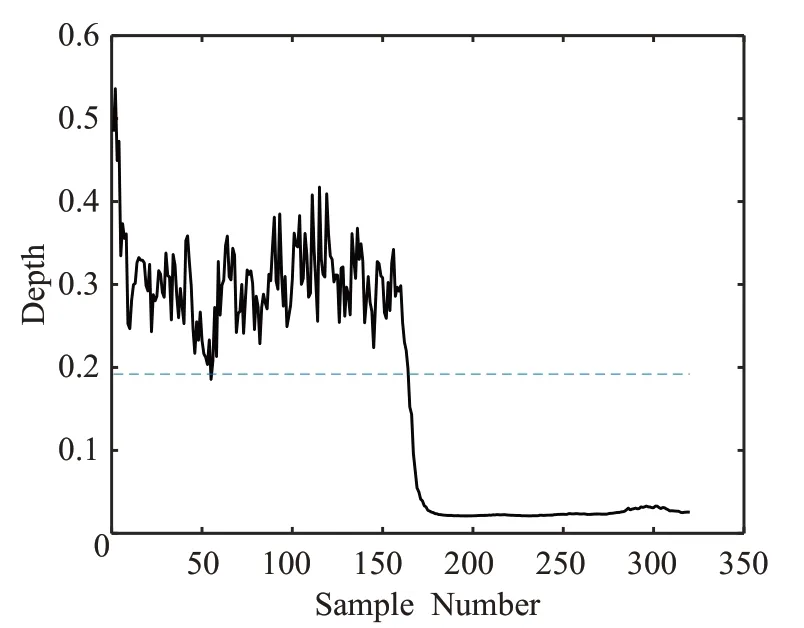
图1 故障1测试集样本的核空间深度值

图2 故障1测试集样本的马氏深度值

为了进行对比，使用主元分析也进行故障检测，步骤如下：

（1）获得正常运行过程下训练集数据X(X ∈Rl×n)，对X 进行列标准化处理，即E(Xi)和std(Xi)分别为列变量Xi的均值和标准差。

（2）对标准化后的矩阵Z 进行主成分分析，根据累计方差贡献度≥80%提取前a 个主成分，对应的主成分方差为λ1,λ2,…,λa,相应的标准正交特征向量为P1,P2,…,Pa，P=(P1,P2,…,Pa)，Σ=diag(λ1,λ2,…,λa)。

（3）对于待测样本根据（1）中E(Xi)和std(Xi)进行标准化处理。

（4）对于（3）标准化处理后的样本数据，计算其Hotelling T2统计量：

（5）控制限阈值为：

比较（4）计算的统计量是否超过阈值，若超过，则该样本对应的工况为故障状态，否则为正常状态。

本例中共500 个训练集样本，原始变量为52 个，提取24个主成分，累积方差贡献度80.51%，取显著性水平α=0.05，对应的控制限阈值为38.83。

由于T2统计量只反映前a 个奇异值对应的得分，而不能反映最小的n-a 个奇异值对应的部分，因而引入SPE 统计量（Q 统计量）。步骤同上，SPE 统计量：

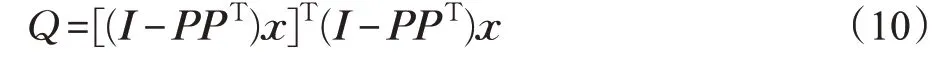
本例中n=52,a=24，取α=0.05，可得SPE统计量的阈值为16.496。图3、4分别为故障1的320个测试集样本基于主元分析的Hotelling T2统计量值与SPE统计量值。

其中，I 为单位矩阵，

图3 故障1测试集样本的Hotelling T2 统计量

图4 故障1测试集样本的SPE统计量

对于故障1，Hotelling T2统计量将156个故障样本识别出来，检测效率97.5%，同时将6个正常样本误判为故障，误报警率3.75%；SPE统计量将160个故障样本识别出来，检测效率100%，但同时将54 个正常样本误判为故障，误报警率高达33.75%。

故障1 是A/C 组分比例扰动，由于反应物A 和C 的比例发生变化，与物质平衡有关的变量（例如液位、压力、成分）的分配关系也会跟着变化，导致超过半数的监控变量明显偏离了它们的正常运行特性[17]，所以很容易被检测出来，除了SPE 统计量有较高的误报警率外，其他三种检测方法的效果都较为理想。

下面以故障4为例进行分析，如图5～8。

图5 故障4测试集样本的核空间深度值

图6 故障4测试集样本的马氏深度值

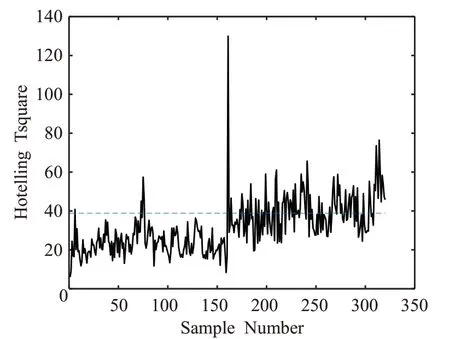
图7 故障4测试集样本的Hotelling T2 统计量

图8 故障4测试集样本的SPE统计量

故障4是反应器冷却水入口变化的一个阶跃变化，当故障发生时，反应器中的温度会突然升高，但其他变量仍保持稳定，与正常运行状况下相比，每个变量的均值和标准差变化小于2%，这使得对此故障的检测比故障1困难得多。

结果显示，使用核空间深度可以将128个故障样本检测出来，检测效率80%，同时仅有1 个正常样本被误判为故障，误报警率0.63%；马氏深度将160个故障样本全部检测出来，检测效率100%，同时将8个正常样本误判为故障，误报警率5%。对于故障4 这种较为复杂的非线性故障类型，本文基于核空间深度和马氏深度的故障检测方法要比分块的主元分析方法（BPCA）、一般的核主元分析方法（KPCA）、基于分块的核主元分析方法（BKPCA）等效果更好[17-18]；而使用Hotelling T2统计量仅能将76 个故障样本识别出来，检测效率47.5%；使用SPE 统计量虽然能达到100%的检测效率，但同时将50个正常样本误判为故障，误报警率高达31.25%，可以看出，主元分析对于这种复杂的强非线性变化所引起的故障是无效的，而基于核空间深度与马氏深度的故障检测方法却能有着良好的检测效果。

对于其他具有代表性的各故障类型，四种检测方法的检测效率、误报警率对比如表1、表2。

表2 基于主元分析的各故障检测结果%

通过表1、表2 可以看出，对于绝大多数故障类型，基于数据深度的故障检测方法都取得了良好的检测效果，并且要优于主元分析的Hotelling T2统计量与SPE统计量检测方法。马氏深度本身相对于Hotelling T2统计量与SPE统计量并无优势，但数据深度作为一种描述多元数据空间分布相对位置的方法，具有明显的非参数稳健特性，使得基于马氏深度的故障检测效果也相对较为满意。核空间深度综合了空间深度的鲁棒性和基于核函数的偏离距离（相似度）的度量，在绝大多数情况下都能取得良好的故障检测效果。

文献[9]也提供了一种基于数据深度的异常检测方法，利用McDiarmid 不等式可以得到相应深度值的阈值，应用于本例中计算得到核空间深度值阈值为0.200 9、马氏深度值阈值为0.011 5。根据文献[9]方法计算的各故障类型检测效果如表3。

表3 文献[9]方法的各检测结果 %

通过与本文所提出的方法的故障检测结果对比可以看出，权衡误报警率和检测效率这两个指标，本文通过构造秩统计量的渐进分布方法虽然简单，但能取得更稳健的故障检测效果，尤其对于马氏深度，在保证检测效率的同时可以降低误报警率，在对过程工业样本数据无任何信息优势的情况下可以达到相对稳健的效果。

5 结束语

本文使用核空间深度、马氏深度这两种数据深度并结合非参数秩统计量，提出基于数据深度的过程工业故障检测方法，通过对TE 过程进行故障检测的建模及与其他方法的对比分析，发现基于数据深度的故障检测结果要比基于主元分析的Hotelling T2统计量与SPE统计量检测效果好，尤其是基于核空间深度的故障检测方法，在多数情况下具有较高的检测效率和较低的误报警率，能取得满意的故障检测效果，可应用于实际过程工业的质量监控，当故障发生时能快速地识别出来，方便管理人员采取相应的应对措施，降低生产风险。