基于车辆配送线路的区域协同配送方法

吴亮然，林 剑，刘毅志，刘 敏

1.湖南科技大学 计算机科学与工程学院，湖南 湘潭411201

2.知识处理与网络化制造湖南省教育厅重点实验室，湖南 湘潭411201

1 引言

物流配送所要解决的核心问题是车辆路径问题（Vehicle Routing Problem，VRP）[1]，传统的解决此类问题的方法多以动态规划方法和启发式算法两种，如扫描算法[2-3]、动态搜索算法[4-5]、遗传算法以及它的改进算法[6-7]等。

随着城市化进程的不断加快，城市辐射面积相应扩大。在城市商业连锁加盟店的物流配送中，存在客户数量大、分布范围广以及客户订单不稳定[8]等特点，传统方法难以满足实际的需求。针对以上问题，国内外的学者也已经做了较多的研究。其中，一些研究内容通过分阶段求解的方式来缩小求解问题的规模，从而来优化配送路径。Liu 等人[9]提出了一种数学规划模型及其相应的图论模型，并设计了一种两阶段贪婪算法来求解实际的大规模物流配送问题，从而最大限度的减少车辆空载运行。Özdamar 等人[10]设计了一种多级聚类算法，将需求点分组为较小的集群，并在集群内部进行具体路径的规划，集群间互相独立，从而得到较优的路由方案。葛显龙等人[11-12]提出网络化跨区域分段联运的方法，设计了不同区域间的“多对多”网络化联合配送机制，打破了传统的分级分区配送方式。黄钰[13]结合客户的需求和时间窗进行客户的区域划分，设计了以油耗成本和车辆固定成本为优化目标的跨区域联合配送模型，并利用改进的遗传算法进行求解。另外，还有一些研究是通过优化配送模型，设计更智能的优化算法，以此进行配送路径的优化。文献[14-15]提出一种双染色体的遗传算法，通过爬山（HC）和模拟退火（SA）来提高解的表现，但相比于一条染色体编码大大增加了解的空间，导致进化速度缓慢。张庆华等人[16]通过改进交叉算子，采用大变异操作来提高遗传算法的搜索速度，但算法的复杂性随之增加。郎茂祥等人[17]提出将爬山算法和遗传算法相结合的方法来求解大规模物流配送问题，有效地避免了算法“早熟”和容易陷入局部最优解的问题。

本文针对单物流中心多区域物流配送中存在的车辆路径规划不合理、装载率不高的问题，提出了一种基于车辆配送线路的区域间协同配送方法。该方法通过配送区域间的空间关系，生成车辆途径配送区域的配送线路。在此基础上，依据配送区域内订单的分布情况和单一区域基于扫描-遗传算法的配送方法，设计了沿配送线路的区域协同配送方法。最后，通过对比实验分析得出，本文所提出的方法，不仅可以减少总配送里程，同时减少了车辆的使用数量，提升了车辆的装载率。

2 问题描述及建模

2.1 问题描述

一般的解决大规模物流配送问题，多是将一个范围较大的服务区域划分成若干个较小的子区域，然后分别在各子区域内求最优解。当区域数量较少、区域内的客户订单较稳定时，这种方法能够较好的满足需求。但是，商业连锁加盟店多区域配送是一个复杂的配送系统，其中区域的分布无规律、区域内订单客户不稳定。因此传统的方法难以对其进行有效的求解。

针对商业连锁加盟店多区域的配送问题，本文提出了沿配送线路的区域协同配送方法，并构建相应的模型。模型需要满足的具体内容如下：

（1）仅有一个配送中心，是每条线路的起点和终点，车辆需从配送中心出发完成配送任务后最终返回配送中心。

（2）每条配送线路上的客户的需求量之和不超过相应配送车辆的最大装载量。

（3）每条配送线路的总长度不超过相应配送车辆的最大行驶里程。

（4）每个客户的货物订单只能被一辆车服务，且仅能被服务一次。

（5）区域内的车辆不仅限于对本区域内的客户进行服务，也可对其他区域内的客户进行服务（区域协同配送）如图1所示。

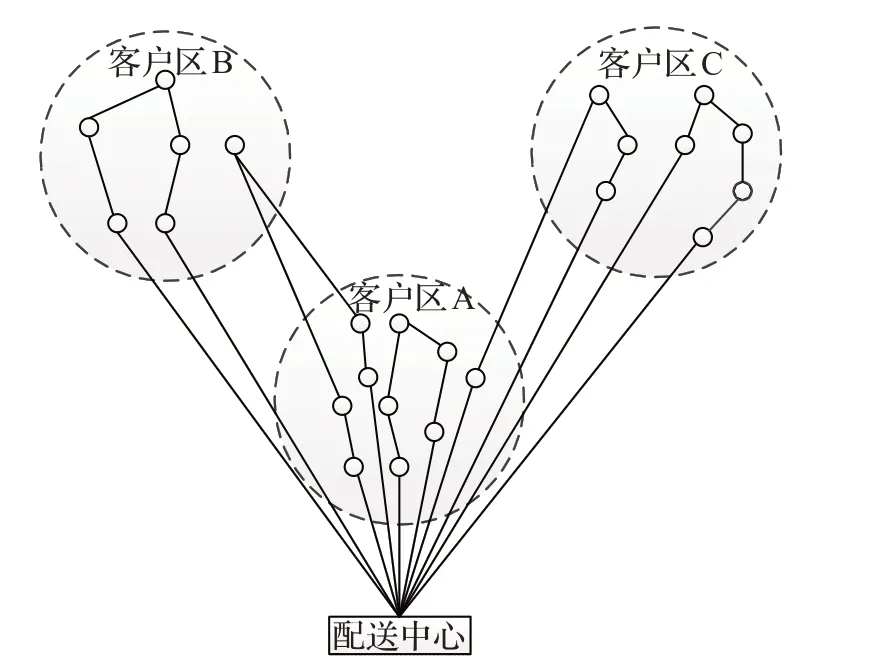
图1 区域协同配送模型

2.2 建立模型

需要的符号和相关变量描述如下。

m：车辆数；

k：第k 辆车；

Qk：第k 辆车的最大装载量；

Lk：第k 辆车的最大行驶里程；

i：第i 个客户；

qi：第i 个客户的货物需求量；

dij：客户i 到j 的距离；

N ：区域数；

I ：第I 个区域；

pI：第I 个区域内的客户数量；

cI：第I 个区域内的车辆数；

则可以建立如下以总里程最短为目标函数的数学模型：

其中，式（1）为以总里程最短的目标函数，表示配送完成后所有车辆的行驶里程之和；式（2）为车辆的最大载重约束；式（3）为车辆的最大行驶里程约束；式（4）表示所有区域客户总和；式（5）表示所有区域车辆总和；式（6）表示每个客户只能被一辆车所服务，且所有的车辆都从配送中心出发完成配送任务后返回配送中心；式（7）和式（8）表示模型中变量xijk和yik之间的关系。

3 车辆配送线路的生成

3.1 线路规划

本文将配送区域（单元区域）抽象成配送线路上的区域节点，用全连通图G 来表示区域的连通情况如图2所示。则令G={ }V,E ，其中V(G)={v0,v1,…,vN}为节点集，v0表示配送中心，vi(i ∈[1,N]) 表示区域节点，E(G)={e1,e2,…,eM}表示各线路节点间边的集合，其中M 表示边的条数。用空间区域拓扑邻接性[18]来反映单元区域间的4种邻接关系如图3。借鉴数据结构中单链表（Single Linked List）的概念来表示配送线路。

图2 线路区域节点结构图

图3 单元区域邻接关系图

现进行如下定义说明。

定义1 线路节点间距离：

其中，wvivj表示节点vi、vj的可达距离。

定义2 区域邻接关系：远邻区域、近邻区域、左邻区域和右邻区域，分别为在不同方位上距离单元区域最近的区域。且每个单元区域的近邻区域、左邻区域和右邻区域的个数均为0个或1个。

定义3 线路链表l ：以单元区域a1为线路的首节点，将其next 指针域指向a1的近邻区域并以近邻区域形成新的节点，继续寻找新节点的近邻区域，直到配送中心v0为止。表示为l={a1,a2,…,an,v0} ，其中ai∈V(i ∈[1,n])如图4所示。

图4 线路链表l 的表示方法

定义4 线路相邻：若两条线路中的某两个区域节点互为左右相邻的关系，则称这两条线路为相邻线路。

3.2 生成协同配送网络

协同配送网络是由V(G)中的每个区域节点到配送中心的线路所钩织出来的网络。由线路链表的定义可知，生成从单元区域到配送中心的线路，关键在于找到每个单元区域的近邻。步骤如下：

步骤1 根据单元区域的邻接关系，找到V(G)中每个区域节点的近邻区域。

步骤2 判断当前区域节点否是为V(G)中的最后一个，若是，则结束；若否，则转向步骤3。

步骤3 根据线路链表的定义，以当前区域节点vi为线路首节点，生成从vi到v0的线路l，并将生成的线路添加到配送网络Γ 中，转向步骤2。

由定义2可知，每个单元区域近邻的个数至多只有一个，则对于生成的配送网络Γ={l1,l2,…,lQ} ，有Q=N 。

3.3 生成初始线路

由于在每次的实际配送任务中，有货区域的数量以及区域内订单的分布情况都不相同，所以在每次的任务中需要根据实际的配送需求，生成此次配送中的初始配送线路。步骤如下：

步骤1 找到此次配送任务中远邻为空的单元区域，并将其设为边缘区域。

步骤2 依据3.2 节生成的配送网络，以及此次配送任务中的区域信息，生成从边缘区域到配送中心的线路集合L={l1,l2,…,lm} ，此时线路中的区域节点均为此次配送中的有货区域。

步骤3 将集合L 中的线路，按边缘区域所在的位置顺时针从左到右进行排序，形成车辆的初始配送线路集合。

3.4 线路间调整

借鉴文献[19]中“节约里程”的思想对具有相邻关系的线路进行如下调整，生成最优的车辆途径配送区域的线路集合。

（1）相邻线路边缘区域调整

举例说明如图5A，线路l1：a1,a2,…,an,v0和线路l2：b1,b2,…,bn,v0中的a1和b1互为左右相邻关系并且存在Da1b1＜Da1a2||Da1b1＜Db1b2。若Da1a2＞Db1b2则调整后的线路为：a2,…,an,v0、a1,b1,…, bn,v0，如图5B；若Da1a2＜Db1b2则调整后的线路为：b1,a1,…,an,v0、b2,…,bn,v0，如图5C所示。

图5 相邻线路边缘区域调整示意图

（2）相邻线路边缘区域和途径区域调整

举例说明如图6A，线路l1：a1,a2,…,an,v0和线路l2：b1,b2,…,bn,v0中的ai和b1互为左右相邻关系并且存在Daib1＜Daiai-1||Daib1＜Db1b2。若Daiai-1＞Db1b2则调整后的线路为：ai-1,…,an,v0、a1,…,ai,b1,…,bn,v0，如图6B；若Daiai-1＜Db1b2则调整后的线路为：a1,…,ai,b1,ai-1,…,an,v0、b2,…,bn,v0，如图6C所示。

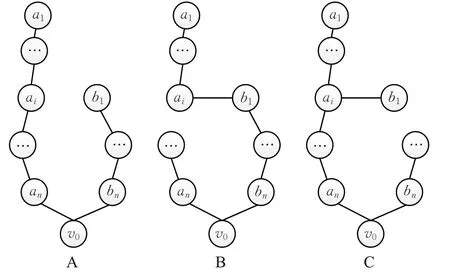
图6 相邻线路边缘区域和途径区域调整示意图

4 配送方法

4.1 扫描-遗传算法的配送方法

这里，选用扫描算法（Sweep Method）和遗传算法（Genetic Algorithm）相结合的方法进行单一区域内的配送。

（1）确定区域扫描方向

举例说明如图7，当进行配送线路l 上的区域A 的配送时，则需根据线路l 上相对于当前区域的下一个区域B来确定A的扫描方向。图中区域A和B存在bc ＞ac&&bc ＞ad ，则区域A 的扫描方向为从b 到a，即从当前区域相对于下一个区域的最远端开始扫描。

图7 确定区域扫描方向示意图

（2）扫描-遗传算法

扫描算法是一种求解物流配送的启发式算法，其基本原理为“先分组后线路”。其中，分组是指为每辆车分配送满足其容量的客户点。线路是指对每辆车所分配到的客户点，采用插入算法、节约算法（Clarke-Wright）等方法进行路径规划，本文采用的是文献[17]中的遗传算法，在此不再赘述。一种简单的分组设计步骤如下：

步骤1 以配送中心为原点，以区域边缘客户点为扫描起点。

步骤2 从原点向起点做射线，并按扫描方向绕原点进行扇形扫描。

步骤3 记录当前扫描到的客户需求qi，并把此次扫描过的客户需求之和S 与当前车辆可装载容量V 进行比较，若S ≤V ≤S+qi则终止此次扫描，把扫描过的需求量之和为S 的客户分为一组，如图8所示。

图8 扫描分组方法

步骤4 重复上述步骤2 和3，直到所有的客户都已分组。

4.2 区域协同配送方法

沿线区域协同配送是指，在每个单元区域内，配送资源共享的前提下，从整体出发进行区域间联合配送，从而达到提高车辆装载率、减少配送里程。具体有如下两种情况。

（1）跨线路配送

根据预先计算出来的当前线路中每辆车的装载率，来判断是否需要实施跨相邻线路的配送。步骤如下：

步骤1 判断当前线路是否有相邻线路，若是，则转到步骤2；若否，则转到步骤4。

步骤2 计算当前线路上车辆的装载率，判断是否有车辆装载率不满足要求（一条线路中最多只可能有一辆车不满足要求），若是，则转到步骤3；若否，则转到步骤4。

步骤3 跨线路配送，计算没有装满的车辆上的已装载量S1和空余量S2，找到当前线路l1和相邻线路l2上距离最近的两个区域节点A和B。在区域A、B中，按扫描法将距离彼此最近的客户分配到跨线路的车上，其中区域A和B装载在跨线路车上的货物量分别为S1、S2，如图9所示。

图9 跨线路配送示意图

步骤4 不进行跨线路配送，在当前线路中，相对于配送中心从远到近，进行沿配送线路的单元区域内配送。

（2）沿线跨区域配送

在进行沿配送线路单元区域内的配送时，当区域内出现没有达到装载率要求的车辆，则让该车辆沿线装载下一个区域内的客户，如图10 所示。为了保证下一个区域内的客户分布的完整性不被破坏，则将该区域内的距离没装满车辆最近一端的客户，通过扫描法分配到该车辆上。

图10 沿线跨区域配送示意图

5 实验与分析

5.1 实验1

为验证模型和算法的有效性，利用“步步高”商业物流管理系统提供的实际配送数据进行实验。其中，配送车辆的额定体积为7.3 m³，装载率的范围为75%～85%，最大行驶里程为600 km。不同尺度下的具体配送数据如表1所示，其中，z 表示有货区域的数量，n 表示区域客户数量之和，w 表示所有客户的货物之和（单位m3）。仿真实验在Intel®Core™i5-6500 CPU@3.20 GHz处理器，8 GB内存，Windows10 64位操作系统下采用jdk1.8.0的编程环境实现。

表1 实验配送数据

表2为在不同尺度下，生成的车辆途径配送区域的线路（数字代表区域编号，如：340124）。

表2 车辆途径区域的配送线路

在单一区域内扫描-遗传算法的基础上，分别通过独立配送模式（IS-G）与区域协同配送模式（CS-G）对实例进行10 次求解，实验结果如表3，其中Best、Worst、Avg、Num和Load F分别代表10次求解中的最优解、最差解、平均解、车辆的平均使用数量以及车辆的平均装载率。

表3 不同尺度下两种配送模式结果对比分析

表3中，在尺度S、M和L下的10次求解中，CS-G相比于IS-G，平均里程的公里数分别降低12.98%、17.32%和13.19%，车辆使用量分别减少2 辆、7 辆和6 辆，车辆的平均装载率分别提升11.49%、18.93%和9.89%。从以上指标的分析中可以看出，相比于独立配送模式，区域协同配送模式在各方面都得到了优化，不仅减少了车辆行驶的总里程，同时提升了车辆的装载率，减少了车辆的使用数量，使得车辆资源使用的更加合理，并有效地减少了交通拥堵和环境污染。实验结果验证了基于车辆配送线路的区域协同配送方法，对于求解多区域物流配送的有效性和现实意义。

5.2 实验2

为进一步验证本文所提出的扫描-遗传算法在单一区域内求解VRP 问题的有效性，选用标准遗传算法（SGA）、禁忌搜索算法（TS）、蚁群算法（ACO）和扫描-遗传算法（S-G），分别对同一区域内的76个客户进行10次配送路径的求解，实验结果如表4，其中Time为10次求解的平均耗时。

表4 实验结果对比分析

从表4可以看出，S-G在最优解、最劣解和平均解这三个指标上要远远优于SGA和TS，在平均求解时间上，相比于这两种算法虽然S-G的耗时最多，但也只是毫秒级的差别，是人们能够接受的范围。同算法ACO 的计算结果相比，S-G 在最优解、最劣解和平均解的计算结果上，虽然只略优于ACO 算法，但在平均耗时的指标上，ACO 的耗时是S-G 的20 倍，且由于ACO 并行算法的本质，在求解配送路径时所消耗的资源远比其他算法要多。从实验结果可以看出本文所提的扫描-遗传算法，对于求解VRP问题的有效性。

6 结束语

本文关注单物流中心大规模多区域的物流配送问题，有针对性地提出了一种基于车辆配送线路的区域协同配送方法。该方法利用配送区域间的空间关系生成区域协同配送网络，进而得到车辆配送线路。在此基础上，依据配送区域内订单的分布情况和单一区域基于扫描-遗传算法的配送方法，设计了沿配送线路的区域协同配送方法。最后，通过对比实验对算法和模型的有效性进行了分析，在不同指标上的计算结果显示，本文方法取得了较满意的效果。