概率不确定语言熵及其多属性群决策

王 宁，朱 峰

郑州大学 商学院，郑州450001

1 引言

为了解决复杂多属性决策中专家偏好的不一致性，Torra 等[1-2]提出了犹豫模糊集。近年来，国内外学者对犹豫模糊集进行了较为广泛的研究和应用，先后将犹豫模糊集拓展为区间犹豫模糊集[3]、对偶犹豫模糊集[4]、犹豫三角模糊集[5]等。在多属性决策过程中，人们对评价方案的属性常常难以给出准确的数字度量，而利用语言评价或不确定语言评价能满足这类决策的实际需求。Rodriguez 等[6]对犹豫模糊集进行了拓展提出了犹豫模糊语言集。虽然犹豫模糊语言集允许一个元素属于某个集合的语言术语可以是多个，但却将每一个语言术语发生的概率看作是相同的。然而，在多属性决策问题中，决策者通常会偏好一些语言术语，使得其具有不同的重要程度。因此，Pang 等[7]提出了概率语言集，不仅考虑到了不同的语言术语，而且给出了其各自发生的概率。目前，概率语言集的研究已引起了愈来愈多学者的关注[8-12]。在实际的决策过程中，由于专业知识和背景的不同，人们对评价对象的认知存在着模糊现象，因而，更倾向于用不确定语言术语进行决策分析。为此Lin 等[13]对概率语言集进行了拓展提出了概率不确定语言集。

为了测量犹豫模糊集和区间犹豫模糊集的不确定性，犹豫模糊熵和区间犹豫模糊熵被引入到多属性决策中。Xu等[14]将模糊熵、交叉熵推广到犹豫模糊环境下，定义了犹豫模糊集的熵和交叉熵，并讨论了两者之间的关系。Farhadinia[15]基于犹豫模糊元的距离测度提出了多种犹豫模糊元的熵。Wei等[16]等结合犹豫模糊元的均值和方差提出了一系列的犹豫模糊熵。Hu等[17]基于犹豫模糊相似度，提出了新的犹豫模糊熵。Zhao等[18]从犹豫模糊元的模糊性和犹豫性两个角度提出了犹豫模糊元的二元熵。李香英[19]首先提出了区间犹豫模糊集的熵和相似度，并分析了两者之间的关系，Alonso 等[20]根据区间犹豫模糊集具有模糊性、犹豫性和信息不完全性的特点提出了区间犹豫模糊集的三元熵。

对于任意一个概率不确定语言集，其不确定语言术语的确定具有一定的模糊性。该语言集是由多个不同的不确定语言术语构成，显示了一定的犹豫性。其次，每一个不确定语言术语的概率不尽相同，具有一定的似然性。并且每一个不确定语言术语本身具有一定的信息不完全性，因此概率不确定语言集的不确定性主要包含模糊性、犹豫性、信息不完全性和似然性。目前关于概率不确定语言熵的多属性决策的研究仍为鲜见。因此，为了测量概率不确定语言集的不确定性，本文首先提出了概率不确定语言集的模糊熵、犹豫熵和不完全信息熵的公理化定义以及相关测度，以分别测量概率不确定语言集的模糊性、犹豫性和信息不完全性。其次，为了能够测量概率不确定语言集的整体不确定性，本文结合概率不确定语言集的模糊熵、犹豫熵和不完全信息熵，提出了概率不确定语言集总熵的公理化定义和相关测度。最后，本文将概率不确定语言熵与VIKOR 方法结合运用到属性权重未知的多属性决策问题中，并通过具体案例进行了验证分析。

2 预备知识

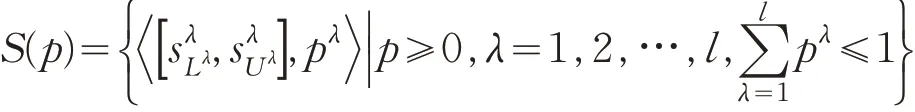
定义1[13]设集合S={si|s0≤si≤sg,i=0.1,…,g}是一个粒度为g 的语言术语集，则概率不确定语言集（PULTS）可定义为：其中和分别是不确定语言术语的上界和下界。l 代表S(p)中元素的个数，而且pλ代表的概率。 S(p)的补集为，其中Lλ和Uλ分别代表和的下标度。

当概率不确定语言集S(p)包含不连续的不确定语言术语且它的概率满足，例如S(p)={＜[s1,s2],0.4 ＞,＜[s1,s3],0.4 ＞}。为了计算的方便，文献[13]提出一种可将其转化为包含连续不确定且概率之和为1的语言术语的标准化处理方法。

首先，要求将不连续的不确定语言术语分成一定数量的连续不确定语言术语，并且将其概率平分。然后为了使概率不确定语言集中的概率和归一化，按照以下方法对其进行处理：

为了计算方便，本文中所有的概率不确定语言集都是经过标准化处理的。

定义2[13]设任意两个经过标准化的概率不确定语言集S1(p),S2(p)，则称

为两个概率不确定语言集的距离。其中δ(λ):(1,2,…,l)→(1,2,…,l)是一种排列，且满足

3 概率不确定语言熵

为了测量概率不确定语言集的模糊性、犹豫性、信息不完全性和整体不确定性。本文将分别提出概率不确定语言集的模糊熵、犹豫熵、不完全信息熵和总熵的公理化定义和一系列熵测度公式。

3.1 概率不确定语言集的模糊熵

定义3 设任意三个概率不确定语言集S(p),S1(p),S2(p)，其中，S1(p)=。一般称函数EFp:S(p)→[0,1]为概率不确定语言集的模糊熵，且满足以下性质：

（1）EFp(S(p))=0当且仅S(p)={＜s0,p ＞,＜sg,1-p ＞}。

（2）EFp(S(p))=1 当且仅当

（4）EFp(S(p))=EFp(Sc(p))。

为概率不确定语言S(p)的模糊熵。且函数f(x):[0,1]→[0,1]满足：（1）f(x)=0 当且仅当x=0或x=1；（2）f(x)=1 当且仅当x=0.5；（3）f(1-x)=f(x)：（4）当x ∈[0,0.5]时，f(x)关于x 为单调递增，当x ∈[0.5,1]时，f(x)关于x 为单调递减。

由于篇幅有限，因此EFp(S(p))满足定义3的证明过程省略。通过改变定理1 中f(x)的表达式可以获得许多类型概率不确定语言集的模糊熵，如：

其中0 ＜t ≤1。

文献[21]认为一个新的熵可以由自变量为已知的熵的函数构成。基于该思想，本文提出一种具有广义形式的概率不确定语言集的模糊熵。相关表达式如下：

定理2 对于任意一个概率不确定语言集S(p)，设EFp1(S(p)),EFp2(S(p)),…,EFpn(S(p)) 是S(p) 的模糊熵，则称

为S(p) 的模糊熵，其中函数Φ(x1,x2,…,xn):[0,1]n→[0,1]满足以下三个性质：

（1）当xi∈[0,1](i=1,2,…,n)时，Φ关于xi单调递增。

（2）当函数值Φ(x1,x2,…,xn)=1 时仅当xi=1(i=1,2,…,n)。

（3）当函数值Φ(x1,x2,…,xn)=0 时仅xi=0(i=1,2,…,n)。

关于Φ(x1,x2,…,xn)的表达式本文给出一些简单的例子，例如：

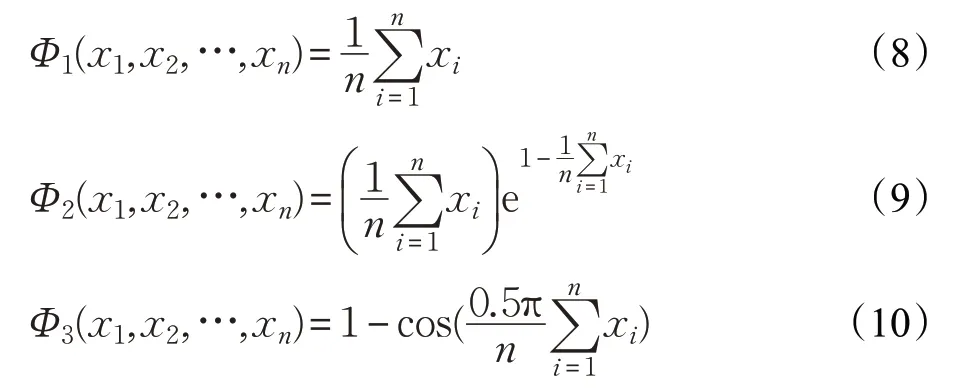
3.2 概率不确定语言集的犹豫熵

犹豫熵的本质是描述概率不确定语言集的不确定语言术语的离散程度。本文认为一个概率不确定语言集的犹豫性可以从以下方面考虑：（1）当不确定语言术语保持不变，而其对应的概率越接近时，则表示不确定语言术语的犹豫性越大；（2）当不确定语言术语的概率保持不变，而它们彼此差异程度越大时，其犹豫性越大。基于以上分析，本文提出了概率不确定语言集的犹豫熵公理化定义和对应的熵测度。

定义4 任意三个概率不确定语言集S(p),S1(p),S2(p)，一般称函数EHp:S(p)→[0,1]为概率不确定语言集的犹豫熵，而且需要满足以下性质：

（1）EHp(S(p))=0 当且仅当S(p)={＜[sL,sU],1 ＞},sL,sU∈S。

（2）EHp(S(p))=1当且仅S(p)={＜s0,0.5 ＞,＜sg,0.5 ＞}。

（4）EHp(S(p))=EHp(Sc(p))。

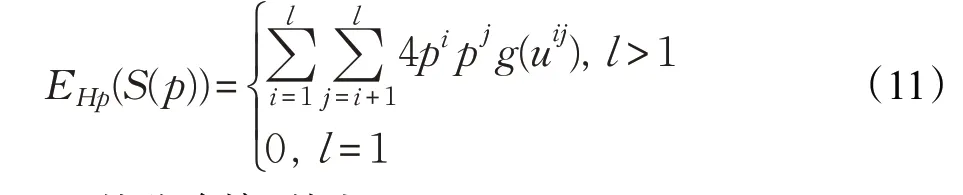
为S(p)的犹豫熵，其中：

同时函数g(x):[0,1]→[0,1]满足以下3个性质：

（1）g(x)=0 当且仅当x=0。

（2）g(x)=1 当且仅当x=1。

（3）g(x)关于x 为严格单调递增函数。

同样关于EHp(S(p))满足定义4的证明过程省略。

通过改变g(x)的表达式可以获得许多类型概率不确定语言集的犹豫熵，如：

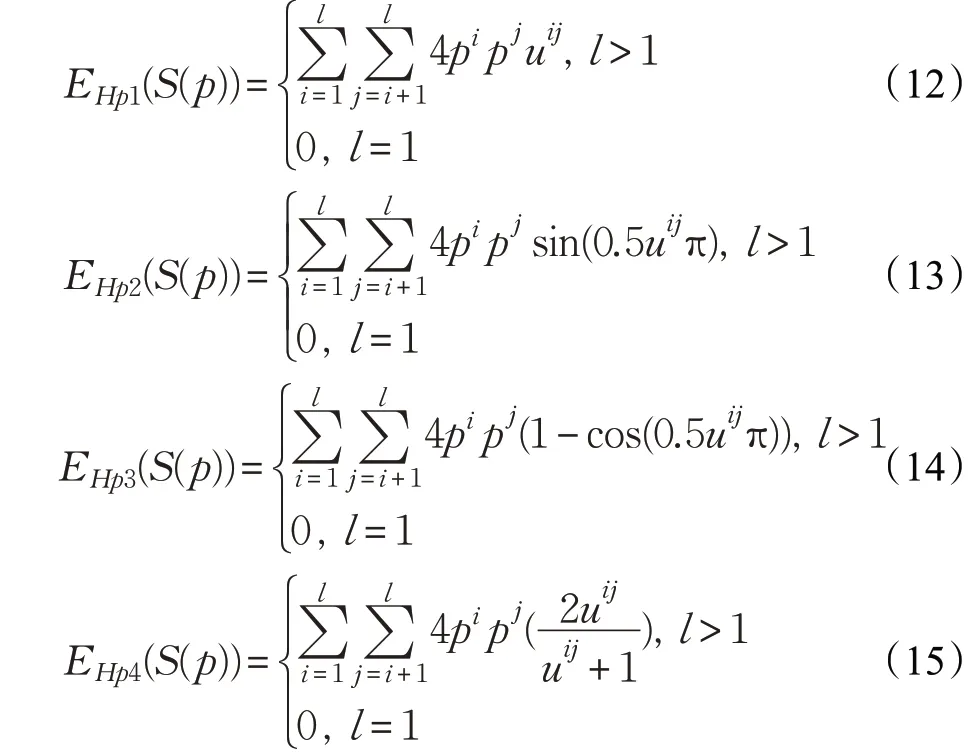
本文基于文献[21]的思想，提出具有广义形式的概率犹豫模糊元的犹豫熵，定义如下：

定理4 对于任意一个概率不确定语言集S(p)，设EHp1(S(p)),EHp2(S(p)),…,EHpn(S(p))为S(p)的犹豫熵，则称

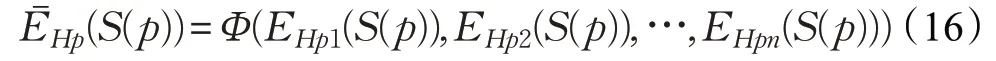
为S(p)的犹豫熵，其中函数Φ(x1,x2,…,xn)同样满足定理2中3个性质。

3.3 概率不确定语言集的不完全信息熵

不完全信息熵是描述概率不确定语言集的不确定语言术语所包含决策信息的不完全性。本文认为一个概率不确定语言集的信息不完全性可以从两个方面考虑：（1）当不确定语言术语的概率保持不变而其下界和上界的差异程度越大，则不确定语言术语包含决策信息的不完全性越大；（2）当不确定语言术语下界和上界的差异程度保持不变，且其差异程度较大的概率越大，差异程度较小的概率越小，则不确定语言术语的不完全信息越多。基于以上两点，本文提出了概率不确定语言集的不完全信息熵，其公理化定义和对应的熵测度定义如下：

定义5 任意三个概率不确定语言集S(p),S1(p),S2(p)，一般称函数EGp:S(p)→[0,1]为概率不确定语言集的不完全信息熵，且满足以下性质：

（1）EGp(S(p))=0 当且仅当

（2）EGp(S(p))=1 当且仅当S(p)={＜[s0,sg],1 ＞}。

（4）EGp(S(p))=EGp(Sc(p))。（5）若和，则EGp(S1(p))≤EGp(S2(p))。

为S(p)的不完全信息熵，其中函数h(x):[0,1]→[0,1]满足以下3条性质。

（1）h(x)=0 当且仅当x=0。

（2）h(x)=1 当且仅当x=1。

（3）h(x)关于x 为严格单调递增函数。

同样关于EGp(S(p))满足定义5的证明过程省略。

通过改变h(x)的表达式可以获得许多类型概率不确定语言集的不完全信息熵，如：

根据已知的概率不确定语言集的不完全信息熵可以得到具有广义形式的新不完全信息熵，相关定义如下：

定理6 对于任意一个概率不确定语言集S(p)，设EGp1(S(p)),EGp2(S(p)),…,EGpn(S(p)) 为S(p) 的不完全信息熵，则称

为S(p)的不完全信息熵，其中函数Φ(x1,x2,…,xn)同样满足定理2中的三个性质。

3.4 概率不确定语言集的总熵

由上文可知模糊熵、犹豫熵和不完全信息熵仅代表了概率不确定语言集的模糊性、犹豫性和信息不完全性。为了全面地考虑概率不确定语言集信息的不确定性，本文根据定义3、定义4和定义5提出概率不确定语言集的总熵以及对应公理化定义。

定义6 设任意三个概率不确定语言集S(p)、S1(p)、S2(p)，函数EˉFp为概率不确定语言集的模糊熵，函数EˉHp为概率不确定语言集的犹豫熵，函数EˉGp为概率不确定语言集的不完全信息熵。一般称函数ETp:S(p)→[0,1]为概率不确定语言集的总熵，而且ETp需要满足以下性质：

（1）当ETp(S(p))=0 时，当且仅当S(p)={＜s0,1 ＞}或者S(p)={＜sg,1 ＞}。

（2）当ETp(S(p))=1 时，当且仅当S(p)={＜[s0,sg],1 ＞}或S(p)={＜s0,0.5 ＞,＜sg,0.5 ＞}。

（4）ETp(S(p))=ETp(Sc(p))。

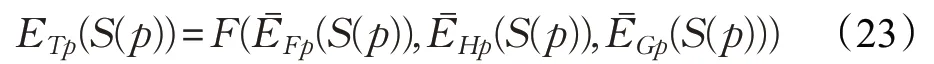
定理7 对于任意一个概率不确定语言集h(p)，则称为概率不确定语言集的总熵。同时函数F(x,y,z):[0,1]3→[0,1]满足以下4个性质：

（1）F(x,y,z)=0 当且仅当x=y=z=0。

（2）F(1,0,0)=F(0,1,0)=F(0,0,1)=1。

（3）设x′,y′,z′是x,y,z的任意位置互换，则F(x,y,z)=F(x′,y′,z′)。

（4）当y,z 不变时，函数F(x,y,z)随着x 的递增而递增的；当x,z 不变时，函数F(x,y,z)随着y 的递增而递增的；当x,y 不变时，函数F(x,y,z)随着z 的递增而递增的。

关于定理7满足定义6的证明过程略。通过改变定理7中的函数F 表达形式，可以获得许多类型的概率不确定语言总熵，例如：

根据已知的概率不确定语言集的总熵可以得到具有广义形式的新概率不确定语言集的总熵，相关定义如下：

定理8 对于任意一个概率不确定语言集S(p)，设为S(p)的总熵，其中函数Φ(x1,x2,…,xn)同样满足定理2中的三个性质。

4 基于概率不确定语言熵的多属性决策模型

利用上述概率不确定语言集的模糊熵、犹豫熵、不完全信息熵和总熵，下面将建立基于四种不确定概率语言熵的多属性决策模型。

对某一概率不确定语言多属性决策问题，语言术语集S={si|s0≤si≤sg,i=0,1,…,g} ，设 方 案 集X={xi|i=1,2,…,m} 、属性集A={aj|j=1,2,…,n} 和属性权重集w=(w1,w2,…,wn)T，其中方案集和属性集已知，而属性权重集未知，则决策步骤如下：

步骤1 首先获得专家的决策结果，其次由于多属性决策问题中属性存在两种类型，即利益型和成本型，前者的属性值越大越好，而后者的属性值越小越好。两种属性值无法进行数学运算，因此需要按照以下规则进行处理：（1）对于利益型属性，其属性值保持不变；（2）对于成本型属性，需要将其转化为利益型属性，即Sij(p)⇒，最终获得了决策矩阵M=(Sij(p))m×n。

步骤2 首先根据式（6）、式（15）和式（21）计算概率不确定语言集Sij(p) 的模糊熵、犹豫熵和不完全信息熵。根据式（25）确定概率不确定语言集Sij(p)的总熵。若属性权重完全未知，则由信息熵理论可知，熵值越小，相应的评价指标越重要；反之熵值越大，则该评价指标越不重要，则属性aj的权重wj的计算公式如下：

如果决策者根据经验能够提供部分属性权重信息，设部分属性权重信息集合为Δ，则可以将决策者提供的部分主观权重信息作为优化模型的约束条件，此外属性的权重应当使得信息熵越小越好[22]，因此建立一个有主观权重信息约束的属性权重确定模型（M-1）：

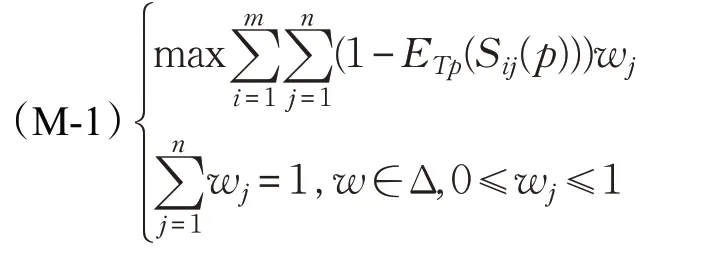
步骤3 根据式（1）分别计算每一个概率不确定语言集Sij(p)与正理想概率不确定语言集S+(p)={＜[sg,sg],p1＞,＜[sg,sg],p2＞,…,＜[sg,sg],plij＞}、负理想概率不确定语言集S-(p)={＜[s0,s0],p1＞,＜[s0,s0],p2＞,…,＜[s0,s0],plij＞} 的距离dp(Sij(p),S+(p))、dp(Sij(p),S-(p))，S-(p),S+(p)中的元素个数会随着每一个概率不确定语言集Sij(p)中元素的个数而定，而且概率pλ(λ=1,2,…,lij)与概率不确定语言集Sij(p)中隶属度的所有概率相等。

步骤4 根据改进VIKOR 方法[23]、属性权重集w=(w1,w2,…,wn)T，dp(Sij(p),S+(p))和dp(Sij(p),S-(p))，计算每一个方案xi(i=1,2,…,m)的群体效益值、个体遗憾值和综合评价值计算公式分别是：

步骤5 分别根据MSi、MRi和MQi对方案进行升序排列，得到三个排序，其中MSi和MRi数值越小，MQi数值越大代表方案越优。

步骤6 确定妥协方案。设MQi按照升序排列得到的结果为x(1),x(2),…,x(m)，如果x(1)同时满足以下两个条件，则为妥协方案：

（2）在依据MSi和MRi进行排列时，x(1)至少有一个依然排列为最小值。

如果上述条件不能同时满足，则可以依据以下情况分别得到妥协方案：如果不满足条件（2），则x(1)和x(2)均为妥协方案；如果不满足条件（1），则妥协方案为x(1),x(2),…,x(m)，其中

5 案例分析

为了便于与已有的方法进行比较，本文选取了文献[13]采用的案例。

5.1 问题描述

假设一家公司邀请五位专家ek(k=1,2,…,5)根据成本a1、可靠性a2、安全性a3、可用性a4和功能a5这五个属性对四种云存储服务xi(i=1,2,3,4)进行评估，并且从中选择最佳的服务。其中a1是属于成本型其他属性均为利益型，五位专家的权重相等，其评估结果用概率不确定语言集的形式表示。其中专家采取的语言术语集为S={s0：极其差，s1：非常差，s2：差，s3：稍差，s4：一般，s5：稍好，s6：好，s7：非常好，s8：极其好}。表1～5分别表示五位专家对这四种云存储服务的评估。

表1 专家e1 的评价结果矩阵

表2 专家e2 的评价结果矩阵

表3 专家e3 的评价结果矩阵

表4 专家e4 的评价结果矩阵

表5 专家e5 的评价结果矩阵

由于专家们的权重一样，根据3.1 小节中对不确定概率语言集的标准化方法对五位专家的评价结果进行处理，然后形成了概率不确定语言决策矩阵，如表6 所示。

5.2 属性权重的确定

5.3 评估方案排序

本文取θ=0.5，根据式（28）、（29）和（30）计算所有概率不确定语言集Sij(p)(i=1,2,3,4,j=1,2,…,5)的群体效益值MSi、个体遗憾值MRi和综合评价值MQi。

根据表7 和步骤6 可以得到对于方案x2，条件1：

表7 各方案的量值及排序

5.4 敏感性分析

在式（30）中偏好系数θ 的取值可能会影响最终的排序结果，因此通过对θ 取不同的数值进行敏感性分析。将偏好系数θ 从区间[0，1]范围内以步长为0.1 取值，分析四种云存储服务评价结果的排序情况。计算结果如图1所示。

图1 θ 值对妥协方案的影响

根据图1的结果可见，随着偏好系数θ 的改变排序结果始终是x2≻x1≻x3≻x4，且经过计算最终得到的妥协方案始终为x1和x2，与上文的决策结果是一致的。由此可见，排序结果对偏好系数θ 的变动不敏感。

5.5 比较分析

为了说明本文模型的有效性，运用文献[13]的方法对评价结果进行比较分析。其中文献[13]分别提出了概率不确定语言TOPSIS（PUL-TOPSIS）法和基于概率不确定语言加权平均算子（PULWA）的多属性决策方法。将以上两种方法的计算结果与本文的计算结果进行比较，其结果如表8所示。

表8 三种方法的结果比较

根据表8的结果可知：虽然本文模型得到的结果与文献[13]中的结果存在部分差异，但本文模型具有以下优势：（1）文献[13]的方法采取离差最大化确定属性权重，而在本文模型中决策者可根据自身偏好选择合适的熵测度进行确权，具有较大的灵活性；（2）文献[13]中的方法假设决策者是完全理性的，而在本文模型中决策者可根据自身偏好选择合适的偏好系数θ 进行决策分析，充分考虑了决策者的心理偏好，更加符合决策者的实际经历；（3）文献[13]的方法并未考虑属性的类型，而本文模型中考虑了属性存在成本型和利益型，因此得到的结果更加合理；（4）文献[13]的方法只适用于属性权重完全未知的情况，而本文模型不仅适用于属性权重完全未知，也适用于属性权重部分未知的情况，适用范围更广。

6 结论

面对概率不确定语言多属性决策的实际需求和概率不确定语言熵的研究仍为鲜见的现状，本文指出了概率不确定语言集的不确定性包括模糊性、犹豫性、信息不完全性和似然性，提出了测量概率不确定语言集模糊性、犹豫性和信息不完全性的模糊熵、犹豫熵和不完全信息熵，并结合犹豫熵、模糊熵和不完全信息熵提出了全面测量概率不确定语言集不确定性的总熵。针对属性权重完全未知的概率不确定语言多属性决策问题，本文应用这四种概率不确定语言熵建立了决策模型，研究结果表明了该决策模型的有效性。在后续的研究中，将关注概率不确定语言集的其他类型的集结算子。