小学数学教材创造性开发的实践与思考

姜华

摘要：教材是引领学生探究的通道，是探究重要问题跳离与回归的站台。基于学生经验的数学教材的创造性开发，是将学科知识下沉，还原至学生的经验世界，是二者的辩证统一;是充分尊重教材，但不拘泥于教材既定的模式，将教材与学生经验发生关联，进入教材的深层，进入学生思维的深层，探究符合学生学习规律的知识体系。

关键词：小学数学教材学生经验创造性开发

教材是教学过程中，教师用来协助学生学习，达到教学目标的各种知识信息材料，是支持学生学习过程的一种资源。但因编写要求制约，大多数小学数学教材呈现的是高度简化的、逻辑性较强的事实性观点，导致学生的学习常常停留于“浅水区”，收获的只是简略的、孤立的事实和技能，难以迈入探究、理解、建构、迁移的“深水区”，形成真实有效的深度学习。对此，我们需要对教材多一些理性思考和深层理解，因“生”制宜，开发利用教材。

一、桥接教材与学生生活经验

生活经验对小学生的学习起着十分重要的作用，是其学习的认知起点，也是其学习的催化剂。贴近学生生活经验的学习素材，最容易引起他们直接的、自发的注意。而教材编排的学科逻辑性，有时会导致教材的编排顺序与学生的认知顺序相反;另外，教材的简化处理通常会隐藏一些问题、观点、思想发展史等，因而所涵盖的信息有时可能会窄化信息化时代的学生生活。这些都易造成教材与学生生活经验的脱节。因此，基于学生的生活经验，适当调整教材的编排顺序并增添适量的主题活动，能够桥接教材内容与学生的生活经验。

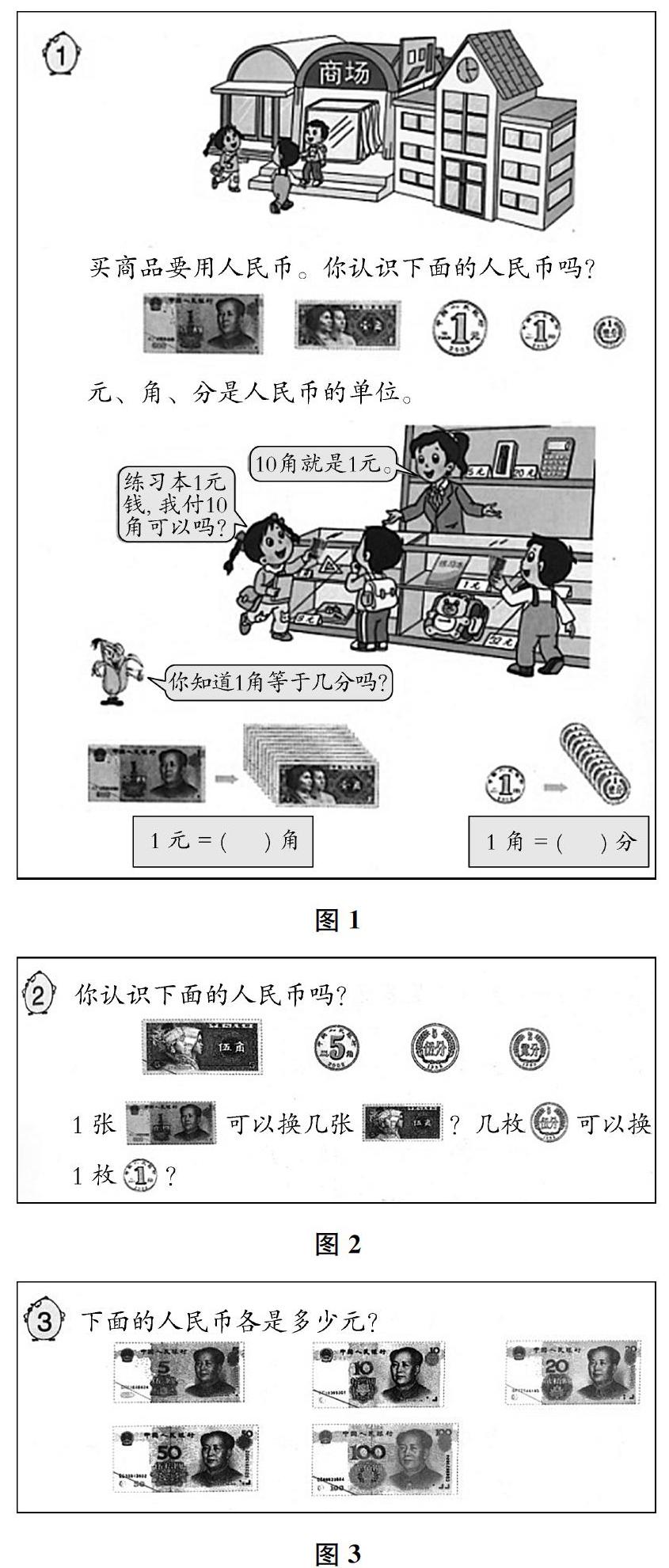
以苏教版小学数学一年级下册《元、角、分》单元为例。人民币的单位“元、角、分”是学生身边真实可感的十进制模型，也是他们学习小数的常用模型，更是后续学习小数的大小比较、加减运算的重要载体。本单元的教学重点是元、角、分的认识以及元、角、分之间的换算。第一课时的例1（见图1）、例2（见图2）主要教学“认识1元及1元以内较小面值的人民币”，第二课时的例3（见图3）教学“认识1元以上较大面值的人民币”。

如今，1角的纸币和5分、2分、1分的硬币已经不在市面上流通，生活中几乎见不到了。教材呈现的文本内容与学生的生活经验之间存在断层，会导致学生在运用的过程中产生困惑。而第二课时的1元以上较大面值的人民币，学生反而更熟悉。对此，笔者对整个单元的教材进行了创造性开发，主要呈现为四次桥接：

1.一次桥接：调整顺序。

尊重学生的生活经验，就应该让学生学习真实可感的数学，而不一定按部就班地学习教材中人为割裂的数学。笔者首先调整了教材内容编排的顺序：先引导学生认识1元以上较大面值的人民币，再认识1元及1元以内较小面值的人民币。因为有100以内整数的认知经验做基础，学习同一单位的较大面值的人民币并熟悉它们之间的换算，对学生来说轻而易举。

2.二次橋接：主题覆盖。

不可回避的是，作为教学内容的目前已经停止流通的小面值人民币，仍需要学生去了解。对此，笔者尝试以“货币的博物馆”为主题设计教学，引导学生查询有关货币的资料，让学生尝试去了解人民币的演变历程以及产生的必要性，初步认识各种面值的几代人民币。在资料查询、信息重组的过程中认识小面值的人民币，了解元、角、分之间的换算，进一步地，还可以了解不同国家的货币及面值，学生学习数学的兴趣得到激发，独立探究的能力得到培养。

3.三次桥接：实践应用。

教材在不同面值的人民币之后，继续编排了《小小商店》的“综合实践活动”，意在让学生在实践活动中经历取钱、换钱、找钱等过程，从而有思考、有探究，并积累感性经验。基于此活动目标，笔者组织全年级开展“跳蚤市场”活动。真实的购物现场，让学生真正地“融入”和“在场”。学生在具体真实的场景中与客观世界对接，发现了巧妙的付钱法，如：购买16元的物品时，可以先付21元，然后直接找回5元，比付20元再找零更方便，这是因为人民币面值设置的特定性引发的“凑整找钱法”。在丰富的购物活动中，“用思维激发思维”，提高学生的应用意识，提升学生灵活运用数学知识和方法解决问题的能力。

4.四次桥接：现实比对。

随着移动支付的普及，人们使用现金的频率越来越低，那么“无现金时代”真的会到来吗？笔者以“支付方式的变化”为主题，引导学生对比、思考、深度探究当前支付方式的利与弊，并畅想未来可能出现的支付方式。给学生一个自由开放的空间，让学生不是止步于课堂教学和实践活动，而是发展更广阔的视野和更深邃的思考。

基于学生的生活经验，调整教材内容的教学顺序，可以让真实的生活经验与学生数学学习的过程有意义地结合;主题的深度覆盖，可以让学生的数学学习过程融合真实的生活经验后充满变化与张力;综合实践活动，可以让学生灵动的生活经验打上数学的底色;现实比对，可以让学生立足当下，思接千载，拥有更广阔的学习空间。

二、桥接教材与学生学习经验

数学教材采用了螺旋上升的编排方式，注重循“序”渐进，旨在让学生在学习当下的内容时会调用先前的学习经验，在建构当下的知识结构时又为下一次的学习做准备。因此，基于学生的先前学习经验，聚焦知识结构中的“干细胞”，多向度地接纳、生成、互融，能够让知识与知识之间具有更强的通联度。

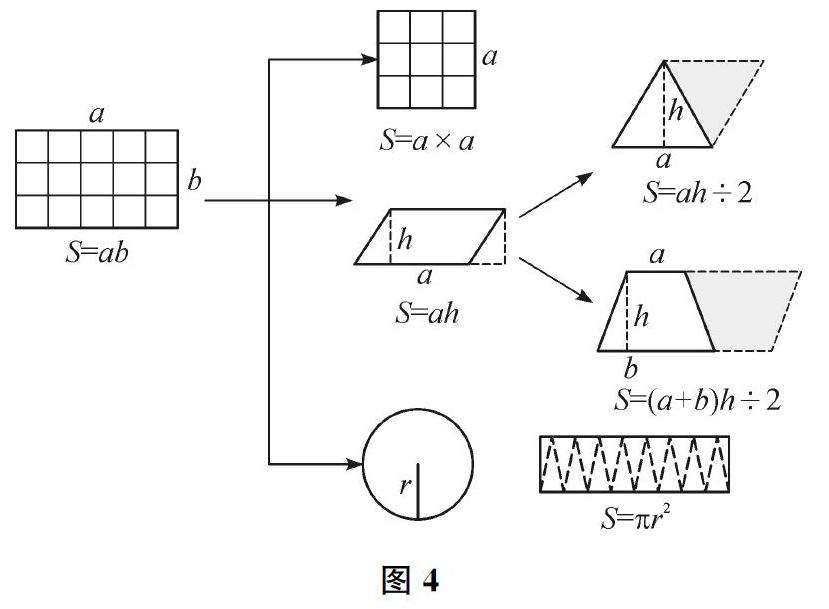
以苏教版小学数学教材中“平面图形的面积”部分内容为例，教材整体的编排思路见图4。从图中可以看出，“长方形的面积”属于该部分内容的核心知识，依托转化思想，教材编排了其他平面图形面积的内容。五年级上册主要教学“平行四边形、三角形、梯形的面积计算”，并以平行四边形的面积作为三角形和梯形面积的生长点。“三角形的面积”的教材内容基本属于任务驱动式的，几乎是直接告知学生用两个完全一样的三角形可以拼出一个平行四边形。这样的编排是因为对很多学生来说，通过对接拼上一个完全一样的三角形来实现转化是难以想象的，而且这种对接方法也与之前学习平行四边形面积的学习经验完全不同。

教材的编排化解了转化的难度，但也埋下了暗示：不存在需要质疑的问题，学生的任务是理解确定的事实。能否给“三角形的面积”的学习寻找一个更为熟悉的生长点？既然“长方形的面积”在“平面图形的面积”部分内容中属于核心知识，具有很强的生长力，那与其他平面图形的面积之间是否有更强的连通度？能否打通长方形和三角形之间的联系，让教材编排的“单向度转化”变成“多向度转化”呢？

1.一次桥接：赋予公式新的意义。

基于以上思考，笔者设计了如图5所示的教学环节。在求第一个直角三角形的面积时，学生想到了割补法、拼补法（见下页图6）。他们初步领会到了将直角三角形拼补成长方形之后求面积更方便，其面积是所在长方形面积的一半。

有了拼补直角三角形求面积的学习经验，在求锐角和钝角三角形的面积时，学生自然想到拼补成长方形的方法（如图7），并推理出三角形与所在长方形二者之间的面积关系：将三角形沿着其中的一条高分成两部分，每一部分都是所在长方形面积的一半，所以两个小三角形的面积之和应该是长方形面积的一半。这种将三角形拼补成长方形求面积的方法也赋予了三角形面积公式S=ah÷2新的意义：a是拼补后长方形的长，h是拼补后长方形的宽。

2.二次桥接：多向度融通。

虽然教材编排的将三角形转化成平行四边形求面积的方法与学生的先前学习经验之间存在断层，但是转化过程有其独特的简便性，值得学生去体会和尝试。如何将这种转化方法巧妙地呈現？能否在前一次建构的基础上，引导学生二次建构，让知识结构得到进一步的丰富呢？笔者鼓励学生继续推想其他证明三角形与其所在长方形面积关系的方法。学生通过推理发现，在拼补的两个三角形S1和S2中（如图8），将S1平移，能与S2拼成一个大三角形，其面积与原三角形的面积相等，所以原三角形的面积是长方形面积的一半。其间，教材意图强调的转化方法呼之欲出。这不仅让学生多了一个求三角形面积的路径，也让他们体会到了探究的乐趣。

尽管按照数学学科逻辑，教材的编排层层深入，但学生先前的学习经验却处于未在场、未唤醒和未改造的状态。数学学习的过程，应是学生的数学经验自我唤醒并不断重构的过程。我们不能把教材看成一成不变的、静态的、线性的“库存知识”，而应基于学生先前的学习经验，聚焦核心与本质，搭建“认知地图”，融通知识结构。

三、桥接教材与学生思维经验

学生经验另一个重要的部分是思维经验。课堂练习是小学数学教学的重要组成部分，重在考查学生对知识的理解以及能否运用所学内容解决问题，是培养学生思维经验和迁移能力的重要载体。练习内容的选取和呈现形式，应尽可能地给学生的思维提供较为广阔的延展空间，不断激发他们的求异思维，促进深度迁移。

以苏教版小学数学教材配套补充习题五年级上册中的一道习题（见下页图9）为例。本题是求解三角形面积的练习中较为经典的题型，综合性强，需要借助正方形的特征和图形之间的关系来寻找求解三角形面积的重要元素：底和高。经典题型往往具有很强的生长力，可以由一道基础题生发出很多变式，是培养迁移能力的优良载体。如何让学生对本题的思考不随着答案的得出而结束，如何让学生在本题中获得的思维经验得到进一步的拓展和延续呢？笔者对本题做了创造性开发（见下页图10）。每位学生有六次构造的机会，比比谁的创意多且独特。

变式中没有提供太多的线索，学生要想完成任务，需要基于对知识和情境的理解，依赖个人的知识迁移能力。面对这样真实的有挑战性的任务，学生被其中所蕴含的丰富的思考所吸引，跃跃欲试，思维也随之被点燃，也因此生成让彼此惊叹的创意（部分学生成果如图11、图12所示）。

为了呈现每一个构造背后的思考，笔者还设计了“最具创意三角形”评选环节。在评选中，学生思维的广度和深度都得到了展现和提升，他们在不断变化的构造中进入了“思维的密林”，将思考提高到了策略水平，使得先前获得的思维经验具有更加广泛的迁移性。

教材是引领学生探究的通道，是探究重要问题跳离与回归的站台。基于学生经验的数学教材的创造性开发，是将学科知识下沉，还原至学生的经验世界，是二者的辩证统一;是充分尊重教材，但不拘泥于教材既定的模式，将教材与学生经验发生关联，进入教材的深层，进入学生思维的深层，探究符合学生学习规律的知识体系。

参考文献：

[1] 曾天山.教材论[M].南昌：江西教育出版社，1997.

[2] 马云鹏.深度学习：走向核心素养（学科教学指南·小学数学）[M].北京：教育科学出版社，2019.

[3] 格兰特·威金斯，杰伊·麦克泰格.追求理解的教学设计[M].闫寒冰，宋雪莲，赖平，译.上海：华东师范大学出版社，2016.学科教育