《简单数阵2》教学实录与反思

闫文娟 狄 飞

【教学内容】

《“学数学 长智慧”超市》“构建等式1”第35～40页。

【学情分析】

根据《构建等式1》本身的编排，我们切分出四节新授课，分别如下表——

选数字构建等式1 第一课时 第二课时 第三课时 第四课时内容 和相等 简单数阵1 简单数阵2小房子数阵简单数阵3正方形数阵样例 □+□=□+□

因此，上本节课之前学生已经有了构建和相等的式子及利用和相等的式子填写简单数阵的基础，在这节课中，希望进一步应用和相等的知识解决数阵问题，进一步积累排除数阵形状干扰，分析实质结构的经验，发展思维的抽象性和灵活性。

【教学重点与难点】

重点：学生能够抽象出数阵中的基本结构□=□+□。

难点：在把握数学结构的基础上，能够有序地得到更多答案。

【教学方法】

提问法、讨论法、示范法。

【教学过程】

一、引入课题

师：把4、5、6、7、8分别填在下图的○里，使每个三角形三个顶点数的和相等。

师：上节课我们填写过一个蝴蝶数阵（如上图），你们还记得是怎么填的吗？

生：左边填4、7，中间填8，右边填5、6。

生：我想这样填，左边填6、7，中间填4，右边填5、8。

生：老师，他们的意思其实就要让左边○里两个数的和等于右边○里两个数的和。

师：为什么只要左边两个数的和等于右边两个数的和就可以？

生：中间这个数是重复计算的数，只要左边的和等于右边的和，再加同一个数，和还是会相等。

生：因为中间这个数是“重复数”。去掉重复数，剩下部分的和相等就可以了。

小结：看来大家都有了经验，我们在填写数阵的时候，要注意分辨“重复数”和“朋友数”。

二、探索新知

1.明确题意。

从1～9这九个数中，选五个填在下面图形的○内，使三角形顶点上三个数的和与正方形顶点上四个数的和相等。

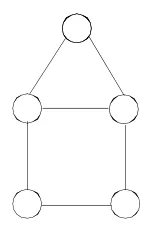
师：谁能跟大家讲一讲，这个题目要我们做什么？

生：三角形顶点上三个数的和等于正方形顶点上四个数的和。

（教师依言演示课件）

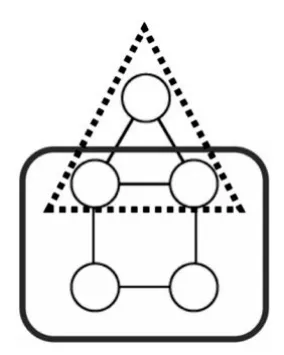
师：大家能不能自己试着来填一填？看看谁的方法好？

2.一次探究。

（1）学生自主尝试三分钟。

（2）反馈与交流。

师：闫老师挑选了几个比较有意思的作业，大家一起来看看。

（展示下图左）

生：他是错的。

师：你怎么知道他是错的？

生：因为他的三角形跟下面的正方形加起来是不相等的。5+2+1=8，2+1+6+7肯定比8大。

师：我们再来读一读题目。

（展示下图右）

生：对了！

师：你们怎么检查出来他是对的？

生：三角形是8+1+2=11。正方形是1+2+3+5=11。三角形数的和等于正方形数的和。

生：老师，我还有一种检查的方法，你们看上面的8正好等于下面的3+5，这样三角形数的和肯定等于正方形数的和了。

师：大家琢磨琢磨，他说三角形这个顶点上的8和正方形这条底边上的3+5相等，整个三角形和整个正方形就相等，你们觉得这样可以吗？

生：老师，我觉得可以。我发现中间这条边是重复加的。

生：它是重复数。它们两个是重复数！

生：房顶上这个数和下面的底边是朋友数。

小结：把蝴蝶数阵里的好办法搬过来了。原来中间是——重复数，而房顶上的○和底边上两个○是——朋友数。

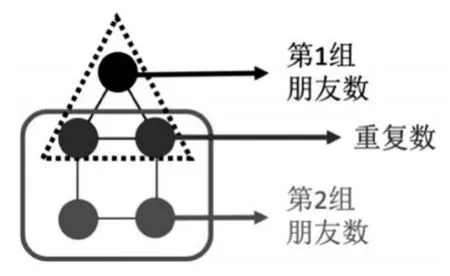
师：这样的话，我们可以怎么检查？

引导检查部分新作品——

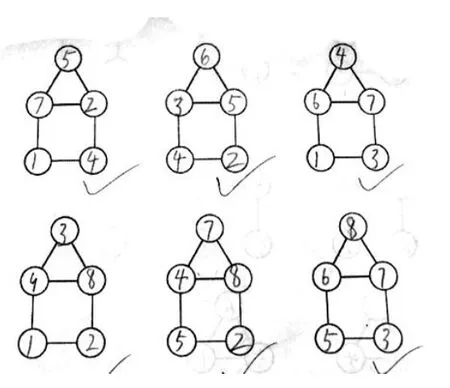
师：那我们填写可以用上什么窍门？

生：朋友数相等，重复数随便填。

生：和蝴蝶数阵一样，先填和相等的部分，再把剩下的数填在重复的地方。

3.二次探究。

师：我们发现了重复数和朋友数的秘密了，那大家是不是能填得更好了？再试一次，我们还用三分钟，比比谁的答案又多又好。

（学生尝试，组织反馈）

师：好了，时间到！你们填了几个？5个？6个？还要多？

师：我们请填得多的同学先来介绍一下，为什么大家都掌握了重复数和朋友数的小秘密，他们会比我们填得多呢？

生：我先写好上面的9，下面写1和8；再写好9，下面写2和7；再写好 9，下面写 3和 6；再写好9……

师：谁听懂他的意思了？他是怎么做的呀？

生：老师，我知道了，这个同学先分解9，上面是9，下面换朋友。

师：那你猜猜他接下来准备分解谁？上面写谁？下面呢？

生：我也知道，我也知道。这个同学接下来上面会写8，下面写1和7；上面再写8，下面写2和6……把8分解完。

师：然后呢？

生：上面写7……

师：那你们觉得这个办法好不好，好在哪里？

生：我觉得很好，他是有顺序的来找一个数，然后拆成两个数的和。

生：我要向他学习，这样就不会重复了。9、8、7、6……

师：这个秘密知道的人还不少呢！这个同学也用到了有顺序定顶点数的办法，可是他比刚才的这位写得还多，这又是为什么呢？（出示部分数阵图）

生：我发现了,他顶点数和底边数不变的时候，中间在换数。

生：他中间换的时候也是有顺序的，有规律的。2和3，3和4，4和5，一个一个大起来。

师：这个同学除了找朋友数有规律，还有什么诀窍？

生：找重复数也有规律，有顺序。

师：那我们照着他的样子写一组7好不好。上面写7，下面可以写？这时候中间——

4.课堂总结。

师：想想我们今天这节课遇到了什么问题？我们是怎么来解决今天这个问题的？这节课你有什么收获？

生：我们发现顶上的1个○等于底下的2个○。朋友数可能是一对一对的，也可能是一个对几个的。

生：我们把中间的两个数有顺序换一换，原来的一种答案就变成很多种了

生：我知道了填写数阵不能光凑数，还是要先看一看有什么秘密，有没有重复数和朋友数，这样填起来又快又轻松。

小结：当我们用火眼金睛看出数阵里的“重复数”和“朋友数”，数阵就变简单了，所以观察题目很重要。另外，知道了原理以后，有序的思考和填写，可以帮我们找到更多答案。

三、教学效果分析

为了验证教学的有效性，我们进行了前后测。

1.课前在未作特别说明的情况下，使用前测题目以了解学生在自发状态下会如何应对“小房子”数阵，以便确定教学的起点和序列。

前测题目是：从1～9这九个数中，选五个填在“小房子”数阵的○内，使三角形顶点上三个数的和与正方形顶点上四个数的和相等。

2.课后立即完成后测题目，以了解本节课的落实度，以及学生仍感到困难的是什么？

后测题目是：从 2，3，4，6，7，9中选五个数填在“小房子”数阵的圆内，使三角形顶点上三个数的和与正方形顶点上四个数的和相等。

3.我们根据学生作品中使用的解题策略，把他们的解题水平描述为五个等级——

零级策略 不会写，都是错的一级策略个别答案是对的，但都是通过完整地计算三角形数的和与正方形数的和得到的，没有有效的策略。二级策略 已经概括出一个顶点数=两个底边数，但书写答案非常随意。三级策略不仅发现一角形顶点数=正方形底边数，而且能有序变化这组朋友数。四级策略概括出三角形顶点数=正方形底边数，不仅朋友数是有序变化的，而且重复数也是有序更替的。

按上述五个等级，统计学生的前测和后测情况发现——

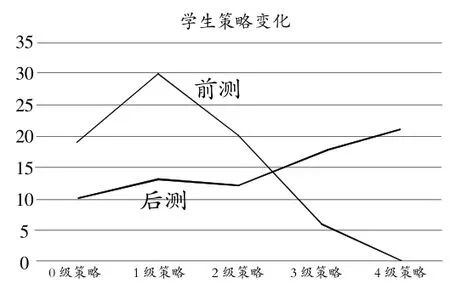
可见，即使后测题目较前测题目在数据设计上明显增加了难度，达到三级和四级策略水平的学生数仍远远高于前测。这不仅说明抽象结构和有序思考不是儿童原生态的思维方式，而且说明，通过合适的训练和交流，儿童能够很快地学习到这样的思维方式，从而大大提升思维水平，提高解题效率。

4.加权平均分。

进一步使用加权平均分的方法整体比较学生在学习前后的解题水平。

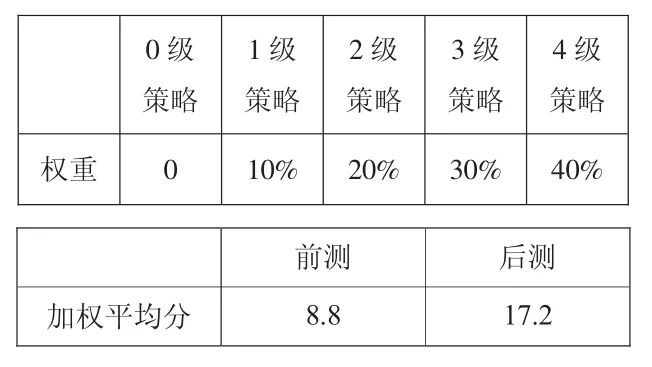
4级策略权重 0 10% 20% 30% 40%0级策略1级策略2级策略3级策略前测 后测加权平均分 8.8 17.2

学生的加权平均分显著提升，前测和后测差异显著，说明学生整体的策略水平都有了提升。

新思维数学一贯主张，不仅要关注儿童学习的现实性，还要开发儿童学习的可能性，我们在填数阵的系列训练中，再次看到，如果设计合适的学习任务，儿童的思维是有潜力的，可训练的。