在提炼中追寻知识的深刻——《立体图形的体积复习》教学实践与反思

陈继辉

【教学内容】

浙教版六年级《立体图形的体积复习》。

【教学过程】

一、注重激活，在现实情境中重温“知识点”

1.复习引入，唤醒经验。

师：（出示图片）同学们，在这幅积木图中，你认识哪些图形？

生：长方体、立方体、圆柱、圆锥。

师：你会计算它们的体积吗？

生：V长=abh，V立=a3，V圆柱=。

生：长方体与圆柱的体积可以用底面积乘高来算。

2.自主整理，回顾推导。

师：它们的体积是怎么推导出来的呢？

生：长方体的体积可以通过底面积乘高来算，因为底面积就是底面所能摆单位小立方体的个数，高就是摆的层数，所以底面积乘高就是单位小立方体的总个数，个数多少，体积就是多少。

生：通过转化法，把圆柱转化成一个长方体来计算。

生：通过实验法，把圆锥装满水倒入同底等高的圆柱中，正好倒了三次。（电脑动画演示）

二、注重梳理，在讨论探究中完善“知识链”

1.全班讨论，沟通联系。

（1）平移。

师：同学们，有没有想过这些立体图形可以通过怎样的变换方式来形成呢？

生：一个长方形向上平移一定的距离，平移走过的轨迹可看成一个长方体。（学生拿着一张A4纸面向全班同学进行演示）

生：一个圆向上平移，它平移走过的轨迹可以看成一个圆柱。

师：垂直平移的距离是立体图形的什么？

生：高。

师：平移的图形就是立体图形的什么？

生：底。

（2）旋转。

师：圆锥可以通过平移这种变换方式来形成吗？

生：不可以。它是通过一个直角三角形绕着它的一条直角边旋转一周形成的。

师：还有其他的立体图形，也是通过旋转形成的吗？

生：圆柱通过一个长方形，以长或宽为轴，旋转一周形成。

生：如果以长为轴旋转，长就是形成圆柱的高，宽就是圆柱的底面半径。

（3）分类。

师：你能不能把这些图形按照形成方式的不同来分类呢？

（学生自主思考后，在黑板上画出韦恩图）

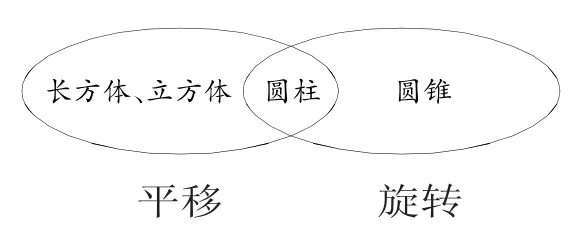
师：哪个图形最特别？

生：圆柱。它既可以通过长方形绕着长或者宽其中一条边旋转360度得到，又可以通过一个圆垂直平移，平移走过的轨迹就是圆柱。

2.分层练习，深化拓展。

（1）基础练习。

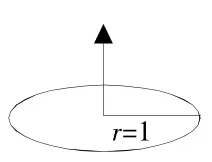
①半径为1厘米的圆，向上平移5厘米，形成的图形的体积是（ ）。

②一个长方形长6分米、宽2分米。绕着它的长旋转一周，形成一个圆柱体，那么这个圆柱体的体积是（ ）。

③一个直角三角形的两条直角边长3厘米和4厘米。以3厘米长的直角边为轴，将直角三角形旋转一周，所得图形的体积是（ ）立方厘米。

（2）提升练习。

下图直角梯形ABCD，以CD边为轴并将梯形绕这个轴旋转一周，得到一个旋转体。它的体积是多少立方厘米？

三、注重提炼，在类比迁移中清晰“知识源”

1.小组交流，提炼共性。

师：（指着长正方体、圆柱）这些立体图形可以通过平移这样的变换方式形成，那还有没有其他图形也是这样形成的呢？（学生先说，教师后出示三棱柱）

师：三棱柱是怎么形成的？

生：我认为可以看作一个三角形向上平移所形成的，三角形就是形成立体图形的底，向上平移的距离就是立体图形的高。

师：它的体积可以用之前的计算公式来算吗？（小组讨论后，派代表汇报）

生：用底面积乘高来计算。

生：因为它们都是通过平面图形垂直平移形成的。

生：底面积就是一层所能摆的单位小立方体的个数，高就是摆的层数。

师：如果三边形变成五边形，接着变成32边形，体积怎么算？

生：还是底乘高。

师：像这种立体图形，我们把它叫做柱体。（板书：柱体）

2.类比迁移，发散极限。

师：随着底面越来越大，变成了什么？

生：圆柱。

师：柱体有相同的计算方法，那么像圆锥这样的锥体是不是也有相同的计算方法呢？

生：有。

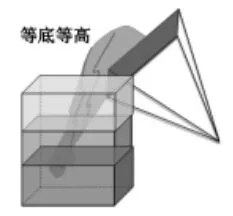
师：以四棱锥为例，猜猜它的体积是怎么推导的呢？

生：可以借助等底等高的长方体，通过倒水实验。

师：你是怎么想出来的？

生：推导圆锥体积时，我们借助了等底等高的圆柱，这里与四棱锥比较接近的是长方体。

师：原来知识之间是有联系的。我们要用联系的眼光去看待问题。建议把掌声送给他。

（电脑实验演示）

师：四棱锥到五棱锥呢？体积可以怎么算？

生：还是底面积乘高除以3。

师：100棱锥呢？慢慢边数多起来，发现了什么？

生：变成了圆锥。

四、注重应用，在解决问题中感悟“知识价值”

1.深刻理解“底”。

师：大正方形的边长是5厘米，小正方形的边长是3厘米，求阴影部分的面积。

生：大正方形的面积减去小正方形的面积就是阴影部分的面积。

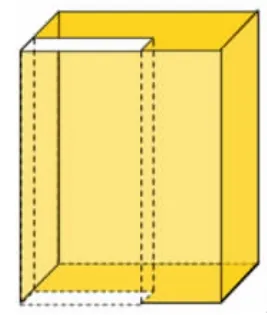
师：如果把阴影部分向上平移6厘米，那么走过的轨迹所形成的立体图形的体积是多少呢？

师：如果想出了一种方法，看看还有没有别的方法。

生：阴影部分体积可以通过大长方体的体积减去小长方体的体积来计算。

生：底面积乘高。底是刚才前面求的阴影部分，高就是平移的距离6厘米。

生：我们可以算出底面可以放16个单位小立方体，总共可以放6层。所以体积等于96平方厘米。

师：底能不能是右边的长方形，高是5厘米，为什么？

生：不能，因为右边的长方形往左平移的过程中，中间有空白部分，不能使得每个面的面积一样大，所以不能成为底。

生：平移过程中，每个面的面积一样大就可以成为底。

2.透过现象，抓住本质。

师：如果把空白部分移到大长方体的这个位置，体积现在是多少？

生：体积不变，因为底面积大小还是大正方形面积减去小正方形面积，高也不变。

师：现在呢？

生：还是一样，高没变，虽然底面形状变了，但大小不变，所以体积不变。

师：是啊！我们要试着学会透过现象，抓住本质，在变化中寻找不变的规律。

【教学反思】

复习课不是简单的重复，而应引导学生厘清知识间的联系，构建知识体系，做到“竖成线、横成片”，使学生更加全面、系统地理解与掌握知识，引导学生独立思考、自主复习，提高解决问题的能力。《立体图形的体积复习》这节课，首先经历复习回顾，进一步理解立体图形的体积概念，掌握计算方法，会解决一些常规的问题；接着经历空间想象与动态演示，从运动变化的角度探索立体图形之间的相互联系，沟通立体图形体积的计算公式，体会共通之处，加深对立体图形体积计算方法的理解；最后提炼共性，体会“在变化中寻找不变量的规律”，渗透联系、类比迁移、极限等数学思想方法。

1.理一理，增加系统性。

本节课通过学生自主梳理立体图形体积推导，全班讨论、从立体图形的运动形成着手，打通知识间的联系，使学生亲身经历、体验知识的再发展，积累数学思维活动经验，实现知识由点到面，增加知识的系统性。

2.练一练，增加灵活性。

通过分层练习，一方面巩固旋转、平移两种立体图形的形成方式，灵活理解不同图形下的底与高；另一方面使“不同学生在复习中得到不同的发展”，让他们在复习过程中都有新的收获。

经历“在变化的现象中寻找不变规律”的过程，通过理解底面积乘高来计算直柱体体积的方法，增加课堂的深度与灵活性。

3.提一提，增加深刻性。

数学复习课除了学习基础知识外，还应适当拓展，鼓励学生自主去发现问题的实质,找出问题的解决方法。本节课，通过引导学生发现直柱体之间、锥体之间具有相同的体积计算方法，深刻理解问题的本质所在，增加课堂的厚度。