透视骰子:玩推理,长思维
□ 罗永军
我喜欢看魔术。有一位网友知道我的爱好,发给我一则魔术视频“透视超能力”:一位魔术师声称他有超能力能看到别人看不到的东西。为验证自己的超能力,他蒙上眼,请一位观众随意掷了一把骰子,随意捡了4颗骰子叠起来,叠在一起的骰子有7个面是看不到的(如图1)。魔术师摘下眼罩看了一眼后,马上就报出这些隐藏面的数字和是24。经当场验证,结果正确!这是怎么回事?观众是“托儿”吗?不太像。观众是随意扔出了一把骰子,并且她在叠骰子的时候动作很快,根本没有时间去看那些骰子的点数。既然不是靠观众的配合完成的,那很有可能秘密就在骰子本身。

图1
一、数学分析
骰子(tóu骰zi子),北方的很多地区又叫色子(shǎi色zi子),是中国传统的玩具,早在战国时期就有,通常作为桌上游戏的小道具。最常见的骰子是立方体骰子,它的面上分别有1-6个小孔(点子或数字),其相对两个面的数字和是7。
点子数为什么不是按数字大小的顺序从1排到6呢?有一种解释是骰子常常用来作为博彩的道具,因此公平是非常要紧的。骰子在滚动时有3个轴向,分别是前后、左右、上下。每个轴向两个面上的小孔总数要相等,即每个轴向的重量相等,这样才会对骰子滚动影响最小。所以每个轴向相对的两个面分别是1和6,2和5,3和4,总和都是7。
根据骰子的排列规律,当桌面上只有1颗骰子,上面的点数是a,那么隐藏在底面的点子就是(7-a)。比如,把2颗骰子叠在一起,如果上面的点子数是6,那么隐藏面的点数总和就是7×2-6=8;如果上面的点子数是5,那么隐藏面的点数总和就是7×2-5=9;如果上面的点子数是a,那么隐藏面的点数总和就是(14-a)。当n颗骰子叠在一起,如果上面的点子数是a,那么所有隐藏面的点数总和是(7n-a)(如图2)。现在我们应该明白魔术师是如何快速地透视骰子了吧。在视频中,魔术师看到观众叠的4颗骰子最上面的点子数是4,他马上就能够算出隐藏面的点数总和就是7×4-4=24。

图2
通过数学分析,我们很容易就能破解这个“透视超能力”的魔术,不过学生能看出其中的秘密吗?
二、认知分析
“透视骰子”实际上是一项数学推理活动。首先是归纳推理——通过观察发现骰子上的数字归纳出规律:相对面的数字和是7。然后是演绎推理——根据1颗骰子上下面的和是7,推导出n颗骰子上下面的和是7n,再根据这一结果减去最上面的点子数最后得出所有隐藏面的点子和。
“透视骰子”还提供了一种跳出思维定式的体验。一般来说,想要知道若干个数的和,通常的方法是把若干个数相加,即由部分数(P)得到整体和(W),这是一种顺向思维。可是,如果这些部分数无法知道呢?有没有办法解决?有。我们可以想这个和在更上位的关系中与什么有关,也就是说跳出固有思维来看,这个底层关系中的和(W)在上位关系中其实是一个部分数(P)。
(一)归纳推理
这个实验适合几年级学生?学生会如何思考?能否顺利地完成归纳推理呢?从运算的角度来看,两个一位数相加的计算是属于一年级的内容,但考虑到还要用到乘法,所以要放到二年级第一学期之后教学。我们选择二、三年级各3个班(每班36人)进行了调查,每人发1颗骰子和1张方格纸,请学生掷一掷骰子,记一记点子数,找一找规律。学生独立操作的时间为3分钟。结果发现,二年级108位学生中有17位发现规律,三年级108位学生中有28位发现规律。也就是说到三年级第二学期,能发现规律的学生不到30%。
那么,其余学生是如何思考的呢?以这颗骰子为例(如图3),学生先是观察了骰子显露在外的5个面分别是1,2,3,5,6,发现还缺“4”,于是就判断底面的数是“4”。这是用排除法来解决问题的,也有推理的成分在内,不过用在求多颗骰子叠加隐藏面的和就难以为继了。

图3
为什么从中发现数量关系那么难呢?我拿了学生记录的3组数据(如图4)请办公室的老师们观察,结果没有一个人发现其中的规律!大家觉得奇怪,这是哪里来的数据?我告诉大家原委并解释了数据的来源(如图5)。有的同事听完之后略想了一会儿就指明了规律:表格中的数是每两个一组:前后之和是7,上下之和是7,左右之和是7,相对两个面上的数字和是7。为什么发现规律这么难呢?大家一起分析了原因,可能以往用来找规律的数据,常常是线型排列:从第1个数开始,每一个后继数都和前一个数有一定的关系,整个数列中的数都是“串”在一起的。而此表格中的数是每两个一组形成数对,它们的排列并不是线型的,每一个数不独立,而是成对排列。像这样呈现数对规律的数列在小学数学中确实不多见,难怪学生没有马上发现。

图4

图5
从观察现象到归纳出蕴含其中的规律,不是一个显然的过程,需要“会主动地建构一些假设,并根据前提提供的证据来评估这些假设的似然性”。在这个过程中,会假设是关键,学生需要有较强的数感,即对数的组合与大小有较强的感悟。
(二)演绎推理
当学生发现“一颗骰子相对面的和是7”这一基本数量关系之后,能不能进一步根据骰子上面的点数推断出隐藏在下面的点数呢?答案是肯定的,108位三年级学生的正确率是100%。不过当2颗、3颗、4颗骰子叠在一起后,求隐藏面的点数和学生感觉还是比较困难的,只有9位学生能独立完成。完成的方法有两种,以4颗骰子为例,有6位是用“7-1=6,3×7=21,6+21=27”,用“7×4-1=27”这一方法的只有3人。显然想到用后一种方法的同学推理能力更胜一筹。对于这样的结果,其实也不意外,毕竟这个年龄段的小学生的思维还处于“具体运算阶段”,对于具体的、看得见的事实能够较好地认知。
皮亚杰把7-12岁(小学阶段)儿童的思维界定为“具体运算阶段”,这个阶段儿童的思维有两个主要特点:开始有守恒观念和能进行群集运算。“透视骰子”的推理活动恰恰需要儿童具备守恒观念和群集运算能力。在这个实验中,虽然我们无法知道每一个骰子上下两个面的点数具体是多少,但我们知道它们的和一定是7(守恒)。从下往上叠放,2颗骰子的数字和是7×2=14,3颗骰子的数字和是7×3=21,……n颗骰子的数字和是7n(群集)。这两项认知能力是数学推理的基础,反过来数学推理活动也能促进儿童在具体运算阶段的思维水平的提升。
三、教学分析
基于以上分析,我们把教学目标定位为帮助学生积淀推理经验。整个实验教学分为两步。
(一)修炼透视眼:寻找骰子点数的排列规律
1.分段看录像:一位魔术师声称自己有超强的透视能力。他请观众把骰子叠在一起,然后很快地说出隐藏面的总和。你觉得他会不会成功?这里把4颗骰子隐藏7个面的情况交代清楚以清晰问题。
2.师:你认为这种能力是天生的还是后来修炼出来的?你准备怎样来修炼呢?我相信每个人都有自己修炼的方式,让我们先从1颗骰子开始修炼吧。
3.学生两人一组进行探究,时间3分钟。
掷骰子时,骰子朝上的数字是随机的,1-6每个数字都有可能出现,学生在实验时感到捉摸不定。图6是学生的一张活动记录单。请注意这张记录单上前4组数据和后5组数据的差别!显然这位学生在前4次活动中没有把骰子的上面点数和底面点数联系起来,转变是在第5次,从第5次开始,他全部“猜”对了!他是怎么发现的呢?在反馈交流时,他说:“刚才3的对面是4,现在(骰子的)上面是4,所以我就知道现在的底面是3。我(根据前面的结果)还知道2的对面是5,1的对面是6,它们加起来都是7。”从这位学生的叙说中可以看出,他的整个思维过程有3个层次,首先是发现骰子朝上的数字重复出现了(如上表中的第2、3列),可以根据前一次结果来确定;其次是发现了所有3组数的位置搭配关系。至此,学生发现了数与位置的关系,这是一种空间位置关系;最后,发现数对之和是7。笔者原以为学生知道了对应关系后,发现“和是7”是很自然的事,然而实际情况是,要推理出数量关系对学生来说还是有难度的,这和前测中了解到的情况基本相符。当有同学汇报时说出“和是7”时,好几个学生情不自禁地点头称是。学生发现“和是7”,看上去只是提升了一小点,但对于处在“具体运算阶段”的学生来讲还真是一个“思维跨越”。
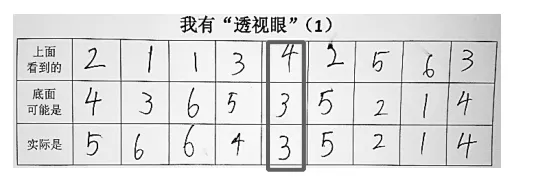
图6
好了,1颗骰子已经能“透视”到底面,那么多颗骰子叠在一起呢?
(二)再炼透视眼:多颗骰子叠在一起求隐藏面的数字和
1.选择骰子。给学生每人准备了4颗骰子,让他们自由选择从几颗骰子开始研究。一方面是希望学生能自己来规划实验;另一方面研究的方法与路径每个人有自己的习惯,没有绝对的优劣之分。事实上,那些掌握了“透视”能力的学生有的是从3颗开始研究,有的是从4颗开始研究,从2颗开始研究的反而是少数学生。从任意点切入进行研究都是可行的,关键还要靠研究者的观察、思考和领悟能力。
2.实验与操作。师生讨论实验步骤:(1)叠一叠;(2)猜一猜;(3)算一算;(4)想一想。两人小组活动,第一次大约5分钟。第二次活动时间视学生探究情况而定。
3.反馈与思考。从第一次活动后的反馈中发现,大约只有10%的学生找到了算法。这个数据和前测结果相同,学生在此确实陷入了困境。他们的困惑是什么呢?
在教学中,我们发现学生往往是先看骰子顶面上的点数,比如顶面是1,然后用7去减,得到这颗骰子的底面数字6,再接下来学生就陷入了困境:继续往下那个面是几呢?它的下面又是几呢?上面的数不知道那么下面的数也没办法知道。于是学生就会忍不住打开骰子去“偷看”。由于每一个骰子朝上的数字是随机的,每次看到的不一定相同,更加让学生对骰子产生捉摸不透的感觉。
其实,学生在“透视骰子”的过程中也用到了“和是7”的数量关系,但只是用在最上面的第1颗骰子上。对于叠在中间的这些骰子,在计算总数时学生还是会纠结每一个面上的数究竟是几,而没有把“和是7”作为一个前提去应用。这表明学生的思维还停留在“要得到总数,必须先知道部分数是几”这个瓶颈中。
学生的思维有可能突破困境吗?除了教师直接讲解外,还能怎么做?
在学生的实验中,我们适时提供了实验单(如图7),提醒学生记录实验数据。有的学生在记录骰子点数写算式时,忽然发现骰子上下两个面不管隐藏着数字几,它们的和都是7,如6+4+3+5+2其实可以这样算:如6+(4+3)+(5+2)或者是7+7+7-1。有的学生对于重复结果很敏感,在记录实验数据(规律连续呈现)中,悟到了关系;也有的学生发现,3颗骰子无论怎样叠放,只要顶上的数字相同,所有隐藏面的数字和也一定是相同的。比如顶面上的数字是1,不管它下面的骰子怎么叠放,所有隐藏面的数字和都是20。增加1颗骰子会怎样呢?如果顶面上的数字还是1,那所有隐藏面的数字和就增加了7,和是27。再增加1颗呢?总和又增加了7,这引起了学生的注意——骰子上下两个面的数字和就是7呀。对实验过程与结果的反思促进了学生对于规律的发现。虽然学生观察与思考的维度不一样,但同样发现了骰子的秘密。

图7
其实我们提供的实验单本身并没有直接的教学功能,但是有了实验单以后学生的思维能够外化为可视化的方式进行分析与再思考。
不过,为什么前后两个实验都是推理活动,但对于学生来说后者会那么难呢?
如果只是从推理要素来判断归纳推理与演绎推理孰易孰难,这比较困难。但如果从数学思维的角度来看前后两个实验,可以发现实际上是两种思维的进化。前一个实验是透视单个骰子,学生发现相对面的数字和是7,利用这个规律可以直接求出隐藏在底面的数,比如用7减几的方法,这是典型的算术思维。而第二个环节的任务是要透视多个叠加的骰子,骰子的个数也不确定,每一个骰子上下面的数字又是随机的,无法用确定数相加来得到隐藏数的和,这就需要用整体关系来解决问题,因此这是一种代数思维。儿童思维从算术思维发展为代数思维是一种跃进,对于处于具体运算阶段的三年级学生来说是有一定困难的。不过,在数学实验这种课程形态中,借助实验材料,让思维可视化,能让学生的数学思维逐渐生长。
有教师可能会提出疑问:学生感觉问题有难度,教师为什么不介入引导呢?比如让学生先从2颗骰子开始研究,全班一起来实验,一起来发现规律,得到初步规律后再来研究3颗、4颗、5颗骰子呈现的规律,最后总结概括。或者引导学生思考怎样算得快,进而把算式中“和是7的数对”用括号标示出来,甚至可以用红笔把它们圈起来,这样就能让学生更好地聚焦规律。我们不反对这样的教法。我们也相信如果这样教学,教学效率一定会提高。但是,我们担心这些引导事实上只是教师以自己的观察和思考代替学生的思维发展,会淡化实验的意义。我们更提倡教师以组织者的身份参与,比如提供实验单、适时组织小组交流、延长学生的探索时间等,让学生有充分的时间和机会去逐渐积累数学活动经验。我们相信这样凝聚而成的数学思维才是活化的、能举一反三和触类旁通的,而这正是数学实验教学的价值所在。

