关注学习过程,再现朴素课堂
□ 吴平付
学生的数学学习应当是一个生动活泼的、主动的和富有个性的过程。但有些教师为了追求所谓的“创新”课堂,追求标新立异,太过注重“形式”和“热闹”,课堂成了教师哗众取宠的舞台,完全失去了课堂教学的本性。《义务教育数学课程标准(2011年版)》中明确指出:有效的数学学习活动不能单纯地依赖模仿与记忆,动手实践、自主探索与合作交流是学生学习的重要方式。学生是学习的主人,教学最终都要落实到学生个体的学习行为上,学生只有通过自己的实践体验、探索、自悟、融合,才能实现再创造,提升数学素养。所以说关注学生的学习过程,再现朴素课堂才是课堂教学生命力的真正体现。
朴素课堂是指基于学生实际,再现学生真实学习过程的课堂。它追求“简洁”“有趣”“有用”和“有挑战性”,它不讲究课堂的完美和面面俱到,力求真实再现学生的学习过程。课堂上有选择,更有舍弃;有所为,更有所不为;以学生有没有进步作为衡量指标。一句话,朴素课堂就是返璞归真的课堂!
一、学习起点的了解是朴素课堂的基础
学生的学习起点是教学的重要财富,是学习新知识的开始。纵观小学数学教材内容,新旧知识之间大多是紧密联系的。教师要着力分析学生的生活经验、知识经验和知识背景,要从学生原有的知识储备出发来设计教学过程,让学生有路可循。如在教学人教版五年级下册“长方体和正方体的体积”这一课时,教师可以联系生活实际,展开教学。
1.认识体积。
首先以学生熟悉的“乌鸦喝水”故事导入,让学生在讨论和交流中初步感悟到石子占有一定的空间;其次通过实验观察发现,不同大小的石子放入同样多的水中水面上升的高度不同,得出物体所占空间有大小之分;最后通过观察三件直观的物件揭示不同物体所占空间的大小不同,从而得出体积的概念。
2.辨析体积。
当学生初步认识体积,能说出洗衣机、影碟机、手机、小石子所占空间大小时,这并不能说明学生已经完全理解了体积。教师拿出两个同样的手机,一个平放在桌面上,另一个竖放在桌面上,问:“哪个手机所占的空间大?”有学生认为横放占空间大,也有学生认为竖放占空间大。教师让学生说说各自的理由。当学生争论没有定论时,教师让一位学生站着,问:“你占的空间有多少?”然后让学生坐下,问:“你现在占的空间又有多大?”通过辨析,学生逐步认识到:同一个物体不管怎样放置,所占空间大小是一样的。
造成学生错误认知的原因,主要是学生受面积概念的影响。体积概念对学生来说是一个全新的概念,是由二维思维转向三维思维的一次跳跃。教师在教学之前对学生的认知有了充分的了解,通过同一物体的不同摆放,插入辩论的环节,既尊重了学生的原有认知,又加深了学生对体积概念的感知和认识,学生参与学习的积极性极大增强。
二、自主探究的激励是朴素课堂的关键
学生参与数学学习的方式有很多,但自主探究的方式更适合学生的认知特点。学生通过亲身经历数学知识形成的全过程,一则对知识的认识更深刻,二则更容易获得成功的乐趣,增强学习数学的自信心。教师就要学会放手,一改“授人以鱼”以“授人以渔”。
如教学“长方体体积的计算公式”一课。学生在认识体积和体积单位时,已经知道了可以通过数体积单位的个数来求长方体体积。教师出示以下活动要求。
1.摆一个体积为12立方厘米的长方体。
2.说一说你是怎样摆的。怎样确定你摆的就是12立方厘米的长方体?
3.与同学的比一比,你们摆的一样吗?不一样在哪里?怎么验证同学摆的长方体体积也是12立方厘米?
4.猜想:你认为长方体的体积跟什么有关?怎样说明你的猜想是正确的?
5.小组合作摆不同体积的长方体,并记录相关数据。

长 宽 高 小正方体的数量 长方体的体积
6.观察上表,你发现了什么?
学生通过上述活动,对体积概念的理解有了进一步的加深。因为这不但是一个活动的操作过程,同时更是一个思考的过程,即学生经历了“数学化”的全过程,在摆放不同长方体的过程中,学生不断猜想、思考,发现每行的个数相当于“长”,行数即“宽”,层数即“高”。通过有趣、有用的探索,水到渠成地得出长方体的体积计算方法。
三、策略方法的优化是朴素课堂的生命
学生在课堂上仅仅学习知识,是远远不够的,还必须学会学习的方法才能主动地获取知识。那么策略方法的优化应该成为教师有意识的“暗线”引导,这主要体现在不同学生在解决问题时会呈现出不同水平的策略方法,教师应在尊重学生个体差异的同时,通过引导,让学生的学习更有方向,同时也让每一位学生对知识进行更好的建构。
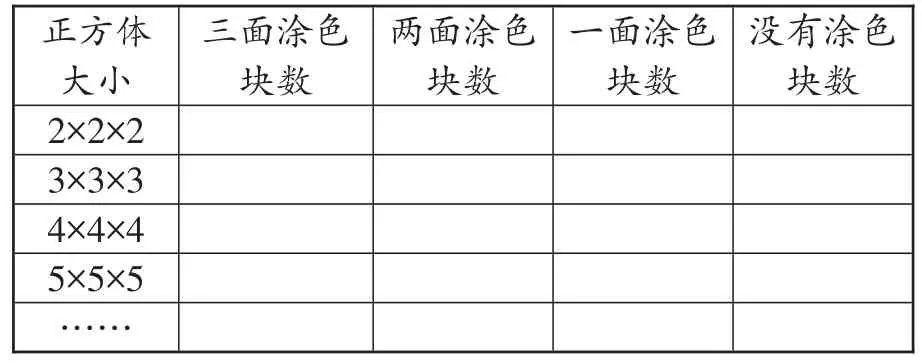
如教学“探索大正方体的涂色规律”这一内容时,教师出示以下活动要求。
1.出示一个用棱长1厘米的小正方体拼成的大正方体(3×3×3),它是由多少个小正方体组成的?说说你的想法。
2.如果把这个大正方体的表面涂上红色,需要涂几个面?
3.思考:这些小正方体会有几个面被涂上红色?根据涂色的情况给这些小正方体分类,可以分成几类?
对于这样的问题,不同的学生解决的方法是不同的。思维层次高的学生可以通过观察、想象就能解决,而大多数学生却无从下手。教师允许学生通过摆一摆、分一分、摸一摸等不同方法来解决,对理解能力不强的学生还允许他们用做记号的方式来完成。
4.如果是4×4×4的大正方体,结果又会是怎样呢?5×5×5呢?
为了便于观察和总结,教师提醒学生可以用表格的形式来记录。
正方体大小2×2×2 3×3×3 4×4×4 5×5×5……三面涂色块数两面涂色块数一面涂色块数没有涂色块数
当学生有困难时,教师提醒学生可以根据3×3×3的正方体来思考:为什么会出现这样的情况,有什么规律吗?如此具有挑战性的问题,激发了学生进一步探究的欲望,学生不再满足于现成的答案。最后通过师生共同的探讨,找到了这类问题的共同规律:
(1)三面涂色的在正方体顶点的位置,因为正方体有8个顶点,所以有8个。
(2)两面涂色的在正方体棱上,除去两端的位置,正方体有12条棱,所以有(每条棱上的小正方体块数-2)×12个。
(3)一面涂色的在正方体每个面除去周边一圈的位置,因为正方体有6个面,所以有(每条棱上的小正方体-2)×(每条棱上的小正方体-2)×6个。
(4)没有涂色的在正方体里面除去表面一层的位置,所以有(每条棱上小正方体块数-2)×(每条棱上小正方体块数-2)×(每条棱上小正方体块数-2),或者用总块数-三面涂色的块数-两面涂色的块数-一面涂色的块数。
学生在“发现规律—验证猜想—总结规律—应用规律”的过程中,初步学会如何探索规律,积累了丰富的数学活动经验。虽然在此过程中,学生获取知识的程度有所不同,但不同的学生都相应感受到了策略方法的优越性,也为以后的探索规律找到了正确的途径和方法。
实践表明,数学教学如果不重视学生的学习过程,只关注答案的获得,那么学生的数学学习就是被动地接受,课堂教学也变成毫无乐趣的“填鸭式”教学,学生的学习能力得不到真正的培养。因此,作为数学教师,一定要重视学生的学习过程,再现朴素课堂,并努力“把课堂还给学生,让课堂焕发生命的活力”。唯有这样,才能体现课堂教学的本性,提升学生的数学素养!

