基于儿童视角的运算教学策略

□ 袁仕理

“数的运算”在人们的学习、工作、生活等方面均扮演着重要的角色，同时也是小学数学教学的重要内容，学好这部分内容对学生后续的发展十分有益。“运算能力”是《义务教育数学课程标准（2011年版）》提出的十个核心概念之一，它指的是能够根据法则和运算律进行正确运算的能力。因此“数的运算”教学应当致力于让学生在理解算理的基础上使用法则进行计算，形成基本的运算技能，并能结合具体情境理解运算的意义及解决实际问题。基于儿童视角展开运算教学，要努力让学生浸润在充满情趣、理趣、智趣的课堂上，既“通情”又“达理”更“育智”，促进学生数学素养的有效提高。

一、以“情”为纽带组织运算教学

每一个数学知识的产生都蕴含着人类丰富的情感和智慧，充满生动的、曲折的探究过程，我们可以将运算教学内容与情境紧密结合起来，为新旧知识找到联结点，创设既切合学生实际又有利于算理理解的情境，进而通过练习设计和组织形式的变化，提高趣味性和挑战性，让学生在迎接挑战的过程中，体验无穷的探究乐趣。

例如，教学“除数是整数的小数除法”时，教师以“说说除法的故事”贯穿全课，按以下程序展开教学：首先，播放图书跳蚤市场小视频，引出问题：5个小朋友合伙开店共收入21元，平均每人分多少元？学生计算后得出：每人分到4元，还剩1元。教师追问：剩下的1元怎么分呢？接着，引导学生用“讲故事”的形式表达解题过程。如，方法一：5个小朋友把1元换成了10角，10角平均分给5个人，每人分到2角，加上原来的4元，一共是4.2元；方法二：在除法竖式中余数“1”的后面添上0再除……方法三：利用计数器演示分的过程，把十位的2换成20个一，平均分成5份，再把个位的1换成10个十分之一，平均分成5份……在“分钱”的故事之后，教师又进一步引导学生思考：除了分钱，还可以分什么？学生提出还可以分“米”、分“千克”、分“数”等等。这样，将枯燥的竖式计算与学生喜闻乐见的故事融合在一起，让数学课堂变得有血有肉，情理交融，既活跃了课堂，又促进了思考。

英国著名哲学家、数学家怀特海在《教育的目的》一书中提出：“说到智力的发展，我要用浪漫阶段、精确阶段和综合运用阶段来描述这一过程。”其浪漫的情感本质上属于“从单纯地接触事实，到开始认识事实间未经探索的关系的重要意义”的一种兴奋。因此，我们要根据儿童的心理特点发挥好“浪漫阶段”的作用，要确立情境为教学服务的观念，运用恰当的情境素材触发情感、触动思维、点亮课堂，使运算教学“出彩”。

二、以“理”为主轴展开运算教学

在运算教学中，我们要重视学生对基本运算概念的理解，注重对数形结合等思想方法的把握，对类比、抽象、猜想等数学思维方式的感悟，在运算教学的课堂上凸显对理性精神的追求。

小学数学运算教学中存在着不少“规定”的内容，如计算方法、书写格式等，它是人们在长期探索和研究的过程中逐渐演变、优化而来的。这些约定俗成的“规定”背后往往隐藏着许多可探究的素材，如“规定”的科学性、合理性、简洁性……教学时可以让学生展开探究，使学生“知其然更知其所以然”。

例如，在“两位数乘两位数”的教学中，教师按以下流程引领学生探索24×12的算理和算法：首先，出示每行24个、共12行的点子图，让学生圈一圈、算一算24×12的结果；其次，展示学生的不同算法，将学生的思维聚焦到以下算法“24×10=240（个），24×2=48（个），240+48=288（个）”；接着，提出问题“像这样先算10行的个数、再算2行的个数，最后相加的算法在竖式计算中也能体现，你能试着列竖式计算吗？”而后，收集了三位学生的竖式计算进行展示：

生1的作品

生2的作品

生3的作品

可以看出，第一位学生受到两位数乘一位数计算的经验影响及点子图的启示直接写出了得数，却缺失了计算过程；第二位学生虽然列出了错误的竖式，但已有了两位数乘两位数竖式计算的影子，在尝试的过程中其实也经历了有价值的思维活动，积累了一定的数学活动经验；第三位学生则将点子图中先分后合的计算方法与竖式计算巧妙地结合起来，“创造”了自己的竖式计算方法。

对于小学三年级学生来说，其思维在很大程度上仍然依赖于感性经验的支撑。在以上教学过程中，教师充分利用几何直观，借助点子图这一可操作的直观材料，使两位数乘两位数的竖式计算与图形表征同步演绎，学生探索“规定”的竖式写法虽然花费了一些时间，但在学生亲历探究的过程中，学生借助直观模型深刻理解了两位数乘两位数计算的道理，自主建构了竖式模型，这样的过程无疑促进了学生学习能力的有效发展。

三、以“思”为主旨深化运算教学

思维能力的培养始终是数学教学的重要目标之一。在运算教学中，知识与技能是学生学习的载体，其中的数学思想方法可能会影响学生的一生。因此，运算教学不仅要立足知识教学，使学生的计算技能得以掌握和提高，而且要充分考虑学生的认知发展规律，在思维培养上要下足功夫，要努力促进学生形成融通的认知结构，着眼数学活动经验的积累、数学思想方法的渗透，致力于学生的可持续发展。

例如，在教学“三位数乘两位数”时，当学生学会竖式计算的方法后，教师出示了这样一道题：这道三位数乘两位数的算式，不小心被滴上了两滴墨水，这道算式的积可能是（ ）。下面四个选项你会先淘汰哪个？

A.453 B.3231 C.30003 D.3213

这个问题激活了学生的思维活动，他们在观察算式特征、整合知识经验、经历思维碰撞的基础上，表达了各自精彩纷呈的看法：有的学生用两个因数的尾数相乘判断，积的个位一定是3，因此淘汰B；有的学生认为三位数乘两位数，积不可能还是三位数，因此淘汰A；有的学生利用估算来判别，把第一个因数估成200，第二个因数估成90，它们的积应该在18000左右，因此淘汰C……这道习题的设计，沟通了口算、估算、笔算之间的联系，将运算技能的培养与合情推理等思维能力的提高有机结合在一起，有效促进了学生运算能力的提升。

小学阶段整数乘法的编排次序为：多位数乘一位数—两位数乘整十、整百数的口算—两位数乘两位数的笔算—三位数乘两位数的笔算。笔者认为，作为整数乘法的“终结课”，“三位数乘两位数”的教学还应注重算理和算法的迁移，要重视知识间的沟通联系，促进学生从整体上建构整数乘法，从而更深刻地理解笔算乘法的本质。本课教学的末尾，教师设计了这样一个环节：“今天我们在原来学过的两位数乘两位数的基础上，进一步学习了三位数乘两位数的计算方法（出示图1），猜猜看：以后我们还会学习什么？”学生脱口而出：“四位数乘两位数、五位数乘两位数……”教师进而出示图2，并提出问题：“这样的算式你会计算吗？”学生在观察后给出了肯定的答复。教师话锋一转：“可是，以后的教材里没有再安排整数乘法了，你知道这是为什么吗？”学生思考后回答道：“因为四位数、五位数乘两位数和三位数乘两位数的方法是一样的。”从而将学生的思维引向发现其中的共同点上，从中感悟这些算式虽然越来越复杂，但算理、算法都是相通的。举一反三、触类旁通的思维能力得到了发展。

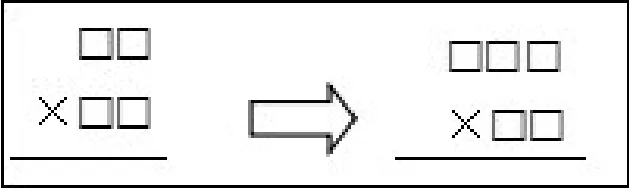
图1

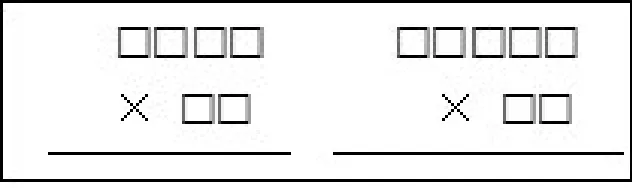
图2

综上，在运算教学中以“情”为纽带契合儿童好奇心、求知欲强的心理特点，以“理”为主轴架设了直观与抽象之间的桥梁，以“思”为主旨促进儿童智力的持续发展。因此，运算教学应当从儿童的视角出发，科学确定教学目标，恰当选择教学素材，合理遴选教学策略，让数学课堂情理交融、智趣相生。