前置探究性作业，促课堂结构转变*——以《圆的认识》一课为例

□任 宁

“圆的认识”是小学阶段“图形与几何”板块中一节经典的概念课，综观各版本教材内容的编排，结合常见教学设计，笔者认为在该节课的学习中有两个问题需要引起重视。

【问题分析】

问题1：涉及知识要点繁多，课堂结构零散。本课中学生要认识圆的外观特征，掌握圆规画圆的方法，知道圆的各部分名称，理解直径半径的关系与特征，知道圆心确定圆的位置、半径确定圆的大小，等等。整节课涉及的知识点较多，也较为零碎，因此，在课堂中很多环节之间联系不够紧密，往往由教师一一推动，显得比较生硬。

问题2：学生已有的相关认知，课中未能体现。根据以往的教学实践经验以及各类前测，发现课前学生对圆的相关知识都有一定程度的了解，比如对圆的各部分名称（圆心、半径、直径）都有所耳闻，知道圆是轴对称图形，对圆规画圆的方法也有所尝试，甚至有学生听说过圆周率、圆周长面积计算公式。但是教师在教学设计时很少考虑学生的已有认知，往往还是按部就班地进行教学。

【课前预测与分析】

如何在教学设计中更好地关注学生的已有认知？如何使课堂教学更加结构化？在学生学习圆的认识之前，笔者布置了前置性的探究作业，以期了解学生的已有认知水平。

（一）前置探究作业设计

圆的认识我知道①关于圆你已经知道了些什么？②请你用圆规画两个大小不同的圆。能说说你是怎么画的吗？你在用圆规画圆的过程中遇到了什么困难？你想得到什么样的帮助？③你能标出下面圆的圆心，并画出它的直径、半径吗？images/BZ_17_1623_1675_1823_1853.png关于半径、直径你还有什么发现？④在边长4厘米的正方形中画一个最大的圆，留下作图痕迹。

（二）前置探究作业分析

（对象：城区A学校五年级学生39人，乡镇B学校五年级学生44人）

1.图像表征的人数多于文字表征，城乡差距不明显

A学校：有65%的学生提到了圆心、直径和半径的名称，有89.7%的学生能够在圆上画出半径和直径的正确图像。

B学校：有63.7%的学生提到了圆心、半径和直径的名称，有81.8%的学生能够画出直径和半径的正确图像。

2.操作技能水平弱于操作方法理解水平，城区操作熟练水平高

A学校：有92.3%的学生会用圆规画圆，但是只有48.7%的学生能够画得比较顺畅，有超过一半的学生认为在画圆的时候针尖会移动，用手指捏住柄旋转一周这个动作比较难完成。

B学校：有95.5%的学生会用圆规画圆，但是只有18.2%的学生能够画得比较顺畅，有超过一半的学生出现手转不过来、画不完整、画着画着就弯了、中心容易移动等现象。

3.直径半径特征不明，定点定长无法理解，城乡各有优劣

A学校：有25.6%的学生能够发现直径和半径的两倍关系。有69.2%的学生通过不断尝试找圆心画最大的圆，但画出来的都不是最大的圆，有些只是比较接近。有33.3%的学生能够用正确的方法在正方形内确定圆心和半径画出最大的圆。

B学校：有40.9%的学生能够发现直径和半径的两倍关系。有40.9%的学生通过不断尝试找圆心的大概位置画出接近准确的图，无人能用规范的方法画出最大的圆。

通过前置性探究作业发现，学生对圆心、直径和半径已经有了直观的认识，只是还不会用比较规范的语言进行表述，那么通过学习教师要让学生用规范的语言对直径、半径的概念进行准确表述；大多数学生已经基本掌握用圆规画圆的方法，只是没有掌握技巧，画得不够熟练，在课中教师应该对画圆方法进行示范，而后让学生通过观察、操作，学会用圆规准确画出圆形；部分学生能够想到直径和半径的关系，而对于直径、半径的特征则没有涉及，因此在课中教师应该引导学生去思考直径、半径的特征；对于正方形中画圆这种探究性作业，大多数学生无法正确操作，主要是因为没有真正理解定点、定长的知识概念，这也是本课的重要学习内容。

【实践策略】

基于以上分析，课堂教学设计可以借助这些前置性探究作业中得到的学生作品资源，进行合理设计，引领学生深度探究圆的知识。

（一）基于学生立场，解决教什么的问题

可以看出，五年级的学生对圆的知识有一定的认知基础，部分学生能够说出“圆是没有角的”“圆没有直线”“圆是一个封闭图形”，也有部分学生知道圆心、半径、直径等名称，虽然不会说具体的定义，但是有直观的表象，能画出相应的图。部分学生也能说出直径和半径的两倍关系，甚至了解直径半径可以画无数条、同一个圆内所有的直径（半径）都相等，但是却无法说出个中理由。基于前置性探究作业的结果分析，我们可以确定本节课的教学重点和难点，哪些应该教，哪些可以弱化。

1.概念理解：重视实践操作，弱化概念表述

在小学阶段，学生学习的是直观几何，不必过分纠结于概念的字词表述。本课中学生要理解半径、直径两个概念，在教学中，我们更要重视实践操作层面的理解，学生能判断、画出相应的直径半径的图像即可。从课前探究作业中发现，多数学生虽不能规范地表述定义，但也能够说出圆心到“圆边”的线段就是半径，说明他们对半径和直径的认知已经趋近规范，教师所要做的就是引导学生把自己的生活化的语言转化为科学规范的语言。

2.特征解析：基于直观感知，渗透深度推理

本课中有一块重要的内容就是直径和半径的特征：直径是半径的两倍；圆内可以画无数条半径、直径；同一个圆内的半径都相等、直径都相等。对于这三条特征，一般学生的认知水平停留在实际操作层面，比如用测量的方法验证直径和半径的两倍关系，同一个圆内所有直径或半径的相等关系，用画图的方式证明可以画无数条半径、直径。对于学生来说，测量和直观操作是最容易想到的办法，但不够严密，比如在测量的时候会出现误差，用画图的方法验证半径和直径可以画无数条的时候，也容易给学生造成“画满”的误解。其实在本课中，还可以引导学生寻找便于理解的、更加严密规范的方式进行验证。比如可以直接通过图示观察得到，直径是由两条半径组成的，因此直径的长度是半径的两倍；根据半径的定义（圆心到圆上任意一点的线段就是半径），因为圆上有无数个点（这个学生是可以理解的），所以从圆心出发到圆上可以画无数条半径，同理推出可以画无数条直径；而所有的半径都相等，则可以借助圆规画圆的过程进行推导，圆规两脚间的距离就是半径，画圆的过程中两脚间的距离不变，所以半径都相等。

3.实践操作：引入不同画法，提炼知识本质

在学生没有学习本课之前，基本都知道用圆规画圆的方法（虽然不一定画得规范正确），但是只出现这样一种画圆方法，对于学生理解圆的“定点、定长”的本质是有所欠缺的。这就需要引入不同的画法——用钉绳工具画圆，这一方法能够更好地帮助学生理解圆的两个要素——定点、定长，以及直观地看到“半径”——绳子，通过两种画法的对比，可以使学生头脑中的图形表征得以显性化，充分体悟圆的本质。

（二）精选课堂路径，解决怎么教的问题

1.前置作业引入，顺应学生心理

本课知识点繁多，课堂结构容易零散，在学生完成前置性探究作业的基础上，利用学生作品引出相关内容的学习，课堂教学环节就会更加流畅。

出示学生作品。

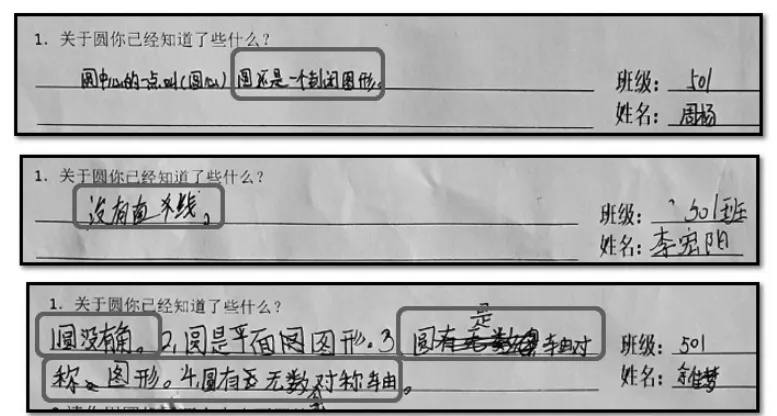
师：请轻轻地读一读同学的作品，谁来说说你读懂了什么？

生：周扬同学说圆是一个封闭图形。

生：圆没有角。

师：没有角是什么意思呢？以前学过的什么图形有角？（生：长方形、正方形）

师：圆没有角，说明圆不是由线段组成的，而是由曲线组成的封闭图形。

生：圆是轴对称图形。

师：请大家拿出圆形纸片，动手验证一下。（学生得出是轴对称图形，对称轴有无数条）

如果没有前置性探究作业作支撑，在课堂上学生的回答要么漫无边际，要么无从谈起，需要教师一步步进行引导，这样的教学环节就会显得零碎，教师的主导作用发挥过度。在解读同学作品的过程中，学生的注意力会更加集中，思维也会更加聚焦，更能够提升课堂教学的效率。

2.巧妙设计情境，改善学习体验

圆心、半径、直径等概念，通常有两种学习方法，要么让学生通过自学直接得出，要么由部分学优生根据已有经验得出，两者都能达到学习的目的，但是都有不足，对于大多数学生来说学习体验不佳。如果能够设计合理的教学环节，激发学生的学习兴趣，那么就会达到事半功倍的效果。

师：刚才大家画了圆，现在老师也来画一个。（在黑板上画到一半借故停止）老师只画了一半，你能帮老师把没画完的圆补充完整吗？

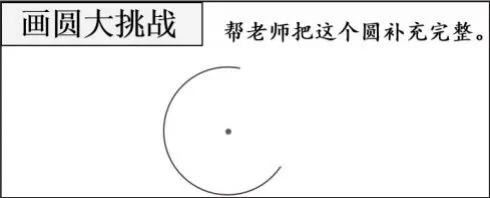
（学生在作业纸上完成补圆操作。之后，教师指名一生上台展示，并说一说是怎么补的。）

生：先把圆规的针尖对准那个点，然后把圆规的两个脚叉开，有铅笔的那个脚对准圆的边，就可以画了。

师：我们回顾一下，刚刚针尖对准的那个点，就是圆的中心点，叫作圆心，可以用字母O表示。

师：如果把刚才圆规两脚叉开的距离画出来，就是圆的半径，用字母r表示。你能试着说一说什么是半径吗？（同桌交流）

师：那么直径是怎样的？（出示概念）谁能上来画一条？用字母d表示。

同样是学习三个概念，如果只是由学优生介绍得出，或者是学生自学得到，显得不够生动有趣，多数学生的学习意愿也不是很强。像这样设置情境，让学生在帮教师补圆的过程中，有了亲身经历的操作体验，关注点就更容易聚焦到圆心和半径上来，那么圆心、半径的概念就呼之欲出，直径的学习自然水到渠成。

3.放慢感悟进度，深入理解本质

圆心决定位置这一知识点，是强行植入，还是操作感悟？半径决定圆的大小这一知识点，是让学生画不同大小的圆，还是画一样大的圆？我们经常可以看到这样的案例。

师：请大家在左边画一个圆，然后在右边画一个圆。（生操作）

师：你看看圆的位置跟谁有关？（或者：为什么一个圆在左边，一个圆在右边？）

生：跟圆心的位置有关。

师：请大家先画一个圆。（生操作）

师：再画一个大一点的圆。（生操作）

师：你发现了什么？

生：圆的大小跟圆规两脚之间的距离有关。

这样的环节设计确实也能够让学生理解圆心决定圆的位置，半径决定圆的大小。但总感觉有些突兀，不利于学生理解这其中的道理。因此，笔者认为可以分两个层次来让学生慢慢感悟。

（1）画一样大的圆

（教师在纸上任意画一个圆，放置于实物投影仪下）

师：谁能来画一个和老师的圆一样大的圆？

生：可以带尺子吗？

师：只带一支圆规。

（生上台演示）

师：他是怎么做的？

生：先把圆规针尖对准老师画的那个圆的中心点，也就是圆心，然后把有铅笔的那只脚对准圆的边，保持圆规两脚距离不动，在旁边画一个圆就可以了。

师：怎么保证画的圆是一样大的？

生：圆规的两个脚之间的距离是一样的就可以了。

“圆的半径决定圆的大小”的结论呼之欲出，但是这时候教师不必急于帮助学生得出结论，暂时让学生处于口欲言而辞不达的状态即可。

（2）长方形内画圆

在课的末尾，可以让学生尝试探究如何在长方形中画最大的圆。虽然有些学生是在不断地尝试中去寻找圆心，而且最终确定的圆心不是非常准确，但也能看到他们先确定圆心的思路。最终成功的方法有两种，一种是用对角线的交点确定圆心，然后以圆心到长方形的长之间的距离作为半径画出最大的圆；另一种是在长方形中间画出“宽”，以“宽”的中点作为圆心，宽的一半作为半径，画出最大的圆。

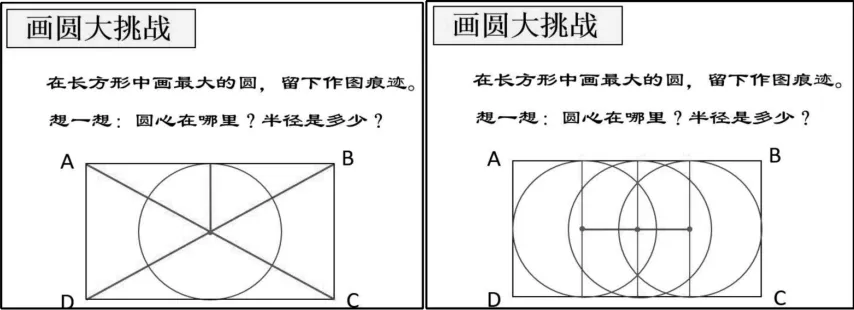
师：请大家观察右图，这些圆有什么一样的地方和不一样的地方？

生：这些圆都是一样大的。

师：为什么？

生：因为这些圆的半径都是相等的。

师：也就是说，圆的大小跟什么有关呢？生：半径。

生：这三个圆的位置不一样。

师：这又是什么原因？

生：因为这些圆的圆心的位置不一样。

师：也就是说，圆心的位置决定了圆的位置。

在长方形中画最大的圆，是一个具有探究意味的问题，这需要学生理解定点、定长的概念，先确定圆心的位置，再确定半径的长度，才能最终确定圆。通过学生的亲身实践，再加上之前画同样大的圆的操作，对于圆心决定位置、半径决定大小的理解自然水到渠成。

本课以前置探究作业为基点，充分了解学生已有知识经验，在此基础上重新确定教学重难点，调整课堂结构，并把前置探究作业的作品合理置入课堂教学环节中，成为课堂教学环节的推进剂，使得整节课重难点突出，凸显学习深度，揭示知识本质，充分体现了探究作业的作用所在。?