基于船舶到港时间预测区间的集装箱码头泊位分配鲁棒优化研究

唐国磊，张 勇

（大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024）

引言

集装箱船舶实际到港时间往往与预计到港时间有一定的偏离[1]，影响码头泊位分配计划[2]，如何利用船舶到港信息做出合理的泊位分配计划，有利于最大限度地利用码头岸线资源，提高客户满意度。

考虑到船舶可能出现到港延误且具有不确定性，一些学者通过引入缓冲时间吸收船舶到港延误时间的不确定性。例如，Xu等[3]引入固定缓冲时间，并应用分支定界法和模拟退火算法相结合的方式获得鲁棒性强的泊位分配方案；Rodriguez等[4]在引用缓冲时间的基础上，应用遗传算法求解最优泊位分配方案。近年来已有研究表明利用决策树、随机决策森林等数据挖掘算法可以获得可利用的集装箱船舶到港延误时间信息，Pani等[5]对 Cagliari集装箱码头船舶到港信息进行聚类分析，利用决策树估计船舶延迟水平；Yu等[6]应用随机森林方法预测得到准确度较高的船舶到港延误（提前）预测区间，这为研究泊位分配鲁棒优化问题提供了重要的输入条件。

因此，在上述研究的基础上，本文提出基于船舶到港时间预测区间的集装箱码头泊位分配鲁棒优化模型，以期减少船舶到港不确定性带来的损失，增加泊位分配计划的鲁棒性。

1 问题描述

泊位分配计划一般表示为时间-空间的二维坐标图。如图1所示，横轴表示靠泊船舶的岸线；纵轴表示时间，矩形表示船舶在时间和空间上对岸线的占用情况，阴影部分表示该艘船舶的缓冲时间。

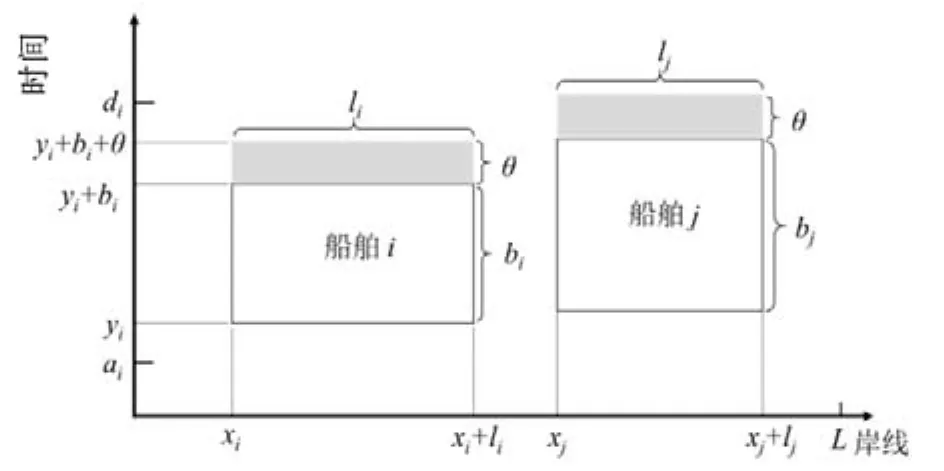
图1 泊位分配计划时空二维坐标

面对船舶到港时间的不确定，本文采用增加缓冲时间的方式提高泊位分配计划的鲁棒性，即在泊位分配计划中增加额外的泊位占用时间来吸收船舶到港时间的不确定性。在缓冲时间段内，该船舶仍然可以占用泊位资源，其他船舶不能与之冲突。

对本文出现的数学符号定义如下：

n-到港船舶总数；

L-泊位岸线长度；

Ai-第i艘船舶到港时间预测区间；

ai-第i艘船舶的预到港时间；

tLi、tRi—第i艘船舶到港延迟（提前）预测区间左、右边界；

bi-第i艘船舶占用岸线时间，包括装卸作业时间、辅助作业时间等；

di-第i艘船舶的预离港时间；

li-第i艘船舶占用岸线的长度；

λ-权重系数，λ∈［0,1］；

M-无限大常数，M→+∞；

xi-第i艘船舶的计划靠泊起点位置；

yi-第i艘船舶的计划靠泊时间；

θi-第i艘船舶的缓冲时间长度；

θ-固定缓冲时间长度。

2 已有的集装箱码头泊位分配鲁棒优化模型

Xu[3]提出为每艘船舶引入固定缓冲时间θ来吸收不确定性的泊位分配鲁棒性优化模型。该模型以最小化船舶离港延迟时间和最大化缓冲时间为优化目标，模型的目标函数和约束条件如式(1)～式(7)所示。

目标函数：

约束条件：

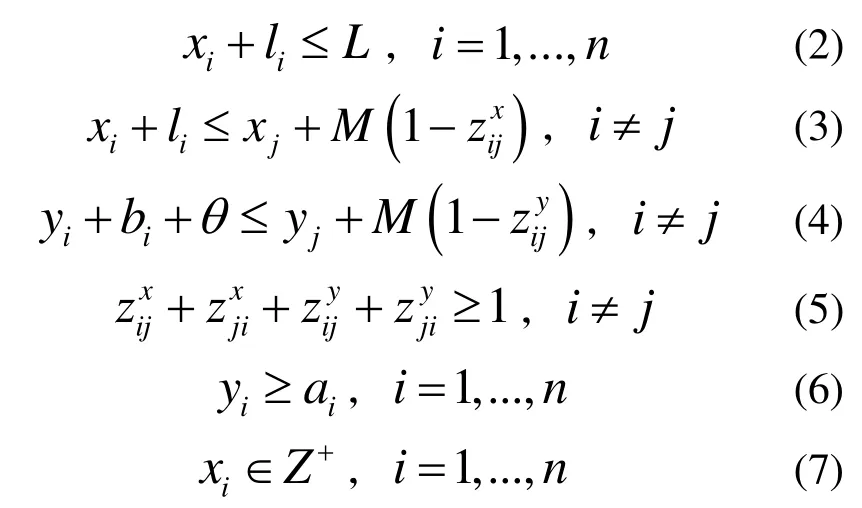
其中，式(1)目标函数由两项组成，第一项为最小化船舶总离港延迟时间，保证船舶在港时间较短，第二项为最大化船舶预留缓冲时间，保证泊位分配系统的鲁棒性，其中，船舶总离港延迟时间越小，则船方在港成本越小，缓冲时间θ越大，调度计划应对船舶到港延迟的鲁棒性越强；式(2)为限制船舶在限定的可停泊岸线长度内靠泊；式(3)、式(4)和式(5)则是限定船舶两两之间在靠泊位置、靠泊时间上不发生冲突；式(6)规定船舶计划靠泊时间大于等于预到港时间。

3 基于到港时间预测区间的鲁棒优化模型

3.1 船舶到港时间预测区间

近年来，一些研究应用随机森林等数据挖掘算法，预测得到可利用的船舶到港延误（提前）时间预测区间[6]。船舶到港时间预测区间Ai为船舶预到港时间ai与到港延误（提前）预测区间之和，即：

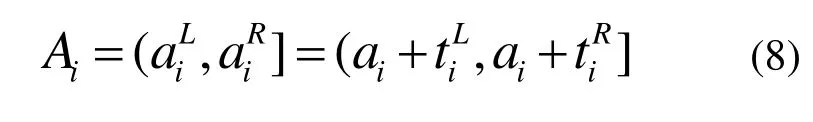
3.2 泊位分配鲁棒优化模型

本文同样以最小化船舶离泊总延迟时间和最大化缓冲时间为优化目标，依据船舶到港时间预测区间Ai分配不同的缓冲时间θi，在保证到港船舶在预离港时间内尽快离港的同时，尽可能增加缓冲时间，提升泊位分配系统的鲁棒性，得到基于到港时间预测区间的泊位分配鲁棒优化模型。

目标函数：

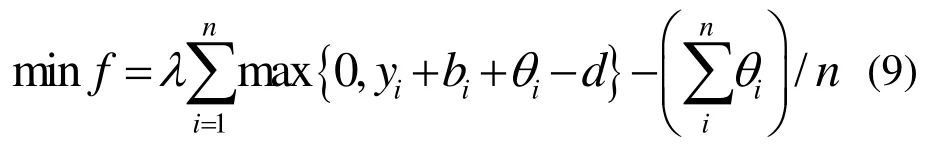
约束条件：

其中，式(13)对每艘船舶增加缓冲时间，并约束船舶在靠泊时间上两两不冲突；式(14)为船舶靠泊时间的下限；式(15)为第i艘船舶缓冲时间的约束，因为缓冲时间是用来吸收船舶延误的不确性[3]。

4 应用实例

以某集装箱港区为例，该港区岸线长度为1 000 m，可停靠20 000 t级至100 000 t级船舶，船舶日到港率为3艘/天，符合泊松分布，各吨级船舶属性及到港比例见表1。根据随机森林算法获得到港延误（提前）区间的预测值，其与延误（提前）区间的实际值的关系见图2。

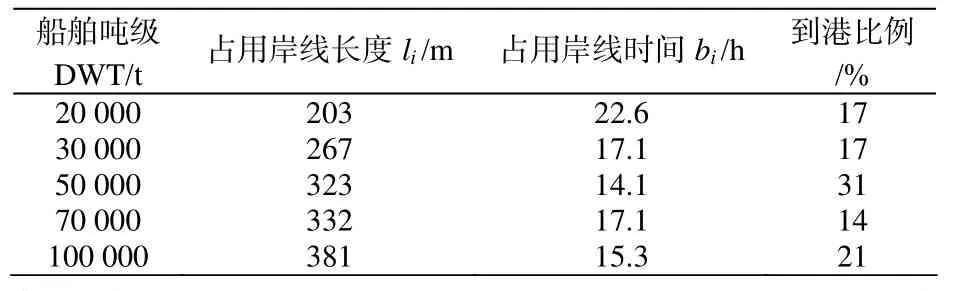
表1 船舶实验参数

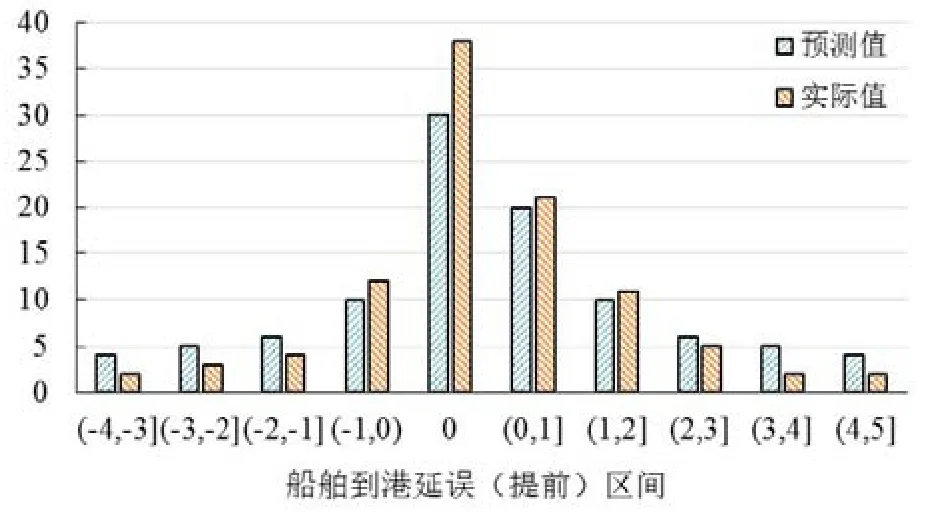
图2 船舶到港延误预测区间概率分布

4.1 实验设置

实验选取20 m作为模型单位长度，以5分钟作为模型单位时间，则模型中岸线长度为50，每日船舶预到港时间ai在区间[0,288]内随机均匀生成，船舶预离港时间为区间[ai+bi,ai+bi+60]内随机均匀生成，船舶延误（提前）时间预测区间和船舶实际到港时间按照图2概率生成，各船型实验参数及生成比例如表1所示。

4.2 验证方法

模型的有效性取决于计划执行的效果。本文采用船舶实际总离港延迟时间RQ指标，表示模型的优化效果，见公式（16）。该数值越小，表示优化效果越好。

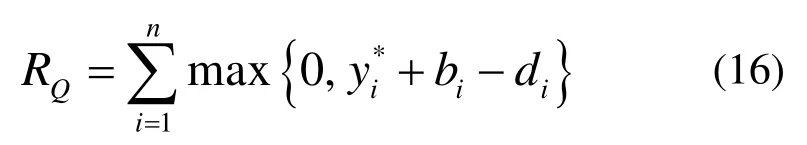
在计划执行阶段，若泊位分配计划能够吸收不确定性带来的影响，则按计划执行调度；否则，调度将采用常见的右移策略[7]调整计划，即推迟未完成的计划，直到不确定性冲突得到解决。

4.3 实验结果比对

为验证本文提出的模型（模型 I）的有效性，与已有的泊位分配鲁棒优化模型（模型II）进行对比。通过模拟10组实验，具体结果如图3所示。

从船舶离港总延迟时间来看，相较于模型II，模型I的船舶离港总延迟时间平均减少15 %。由此可见，本文提出的模型I由于考虑了船舶到港时间的预测区间，提高泊位分配计划的鲁棒性。

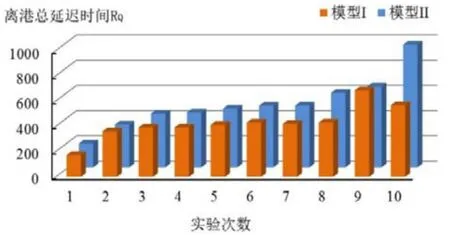
图3 模型离港总延迟时间对比

5 结语

考虑到船舶到港时间具有不确定性，本文将船舶到港时间预测区间作为输入，并为对每艘到港船舶增加缓冲时间，建立基于船舶到港时间预测区间的集装箱码头泊位分配鲁棒优化模型。结果表明本文提出的模型可以提高泊位分配计划的鲁棒性，减少船舶离港延迟时间。