组合矩形港池振荡特性研究
郑振钧,马小舟,董国海
(大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024)
引言
港湾振荡是发生在封闭或半封闭水域的一种很常见的驻波现象,当外界扰动频率与水域本征频率一样或接近时会产生剧烈的水面振荡和周期性流场,在港口、海湾等人类活动密集的水域造成危害[1-2]。港湾振荡灾害的发生与否,要同时考虑港口的内因和外因,即港口本身的振荡特性和当地的波浪条件。港口建成后,平面形状和水深不会轻易改变,因此振荡特性就基本确定了。只有港口所在海域的波浪要素匹配上港口的本征频率时才有可能引发共振。此外,港湾振荡灾害的重要体现是船舶损坏,这与船舶运动特性密切相关,因此港口的设计船型也应给予考虑。
港湾振荡的研究多着手于单港池情形,而多港池(耦合港池)情形更符合实际,但获得的研究相对较少。Lee和 Raichlen[3]使用边界元法求解Helmholtz方程,进行了大量的耦合港池数值实验。结果表明,整体上耦合港池相对于单港池有着更大的放大因子和更复杂的响应曲线。Losada等[4]在水槽中做了双侧矩形港池模型实验。结果表明,在能使单个港池产生共振的入射条件下,同时开启另一个港池,会使原来港池的共振减弱,但减弱程度与另一个港池的长度并没有明确的关系。Bellotti[5]通过线性长波方程研究了理想港口在长波作用下的瞬态响应,两个小口门矩形港池相连情形的数值结果表明,外池的存在使内池的本征频率发生了偏移和个数的增减,同时使港口变得更加的封闭,一旦发生共振,能量很难疏散出去。Xing[6]基于缓坡方程探讨了花莲港的共振改善措施,包括港池分割、打断或新增防波堤、增加消能边界等,总结了减弱港湾振荡的三种思路,第一种是改变港池形状,使得共振频率偏移,不与当地波况和船舶响应频率匹配。第二种是采取减弱长周期波动的措施,但通常很难快速地消减长周期波动。第三种为前两种的结合,改变港池形状使共振峰平移到高频区域,再采取对高频区域更为有效的消除长周期振荡的措施。
综上所述,耦合港池的振荡十分复杂,规律难以探明。耦合港池往往形状复杂、可调参数较多,因此多港池的研究主要关注于实际港口,其成果对该港口有很强的依赖性。如何进行多港池的振荡研究并找到其共性,使成果能较好地应用于普遍的多港池港口,是耦合港池研究的重点和难点。矩形港池是最为常见的港池形状,本文针对多种矩形港池组合展开研究,主要关注两个问题,一是新建矩形港池对响应曲线和模态有什么影响;二是港口会变得更安全或更危险。
外海水深依据不同的实际情形会有巨大差异,在研究中难以选择具有普适性的水深变化形式。同时,外海变化的水深主要导致波浪的折射和浅化,影响到达港口波浪的波向和波幅,对波长的影响很小。就研究港口的内因而言,外海水深的变化形式并不重要。为简单起见,在多矩形港池耦合振荡研究的起始阶段,港内外水深取为常水深。
1 数值模型及验证
本文采用 Chamberlain等[7]推导出的拓展型缓坡方程,相对于 Berkhoff[8]推导出的经典椭圆形缓坡方程,添加了地形的曲率项和坡度平方项,可改善方程对快变水深的适用性,表达式为:

式中:f1和f2为kh的函数,k为波数;C和Cg为波浪相速度和群速度;φ为速度势函数;g为重力加速度;∇为平面微分算子。
上述缓坡方程属于椭圆形偏微分方程,非常适合用有限元方法进行求解。有限元方程的导出和数值求解可参考文献[9]和[10]。模型的验证选择 Wang等[11]基于线性长波方程推导出的斜底细长港解析式。港池布局见图1(a),实心圆为波高测点,固边界为全反射直立壁面。水底坡度为1:40,外海水深0.75 m,内墙水深0.25 m,见图1(b)。港池特征长度为20 m。响应曲线对比见图1(c),结果吻合地很好。其中,纵坐标称为比波高,横坐标为波数与特征长度的乘积,与频率类似,横坐标越大代表周期越小。比波高随着横坐标的变化称为响应曲线,每个极值对应一个本征频率,本征频率和相应的比波高分布称为本征模态。
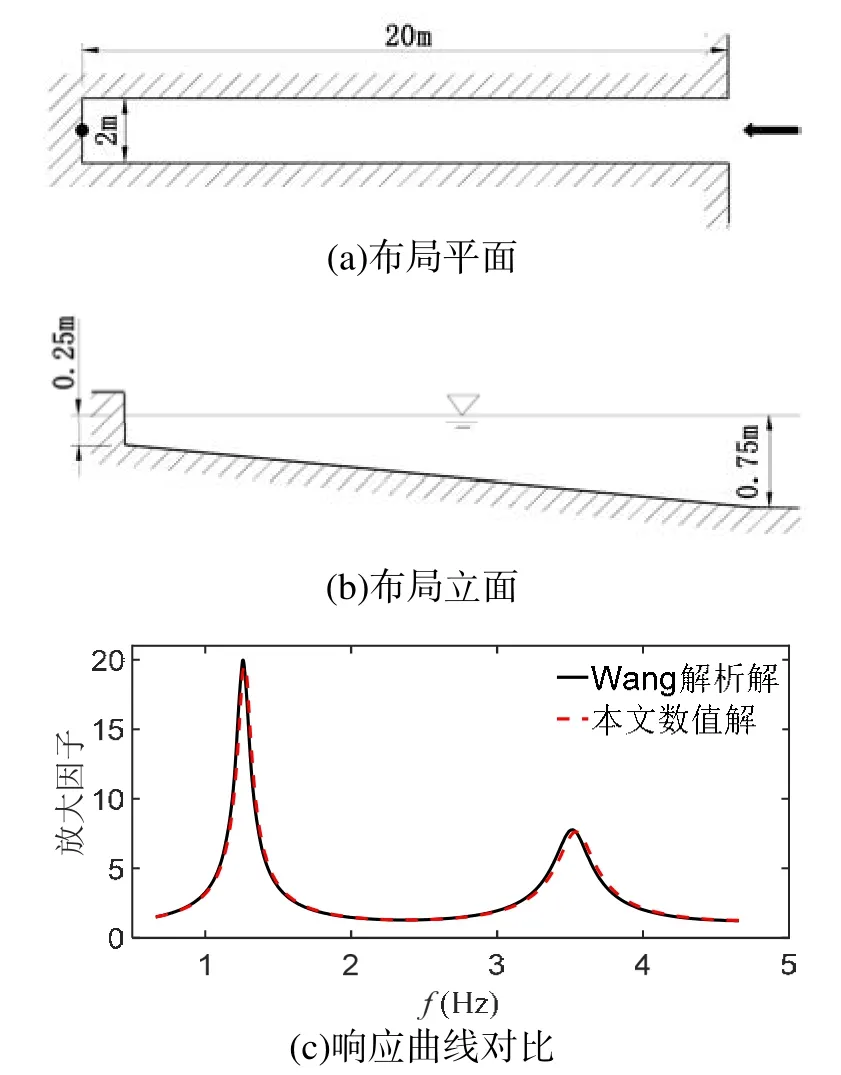
图1 模型验证算例布局和结果对比
2 矩形港池组合
本节的组合矩形港池见图 2,固边界为全反射的直立壁面,波浪都以斜向45°入射,波向示意见图2(a),水深皆为10 m。图中实心圆为测点,港池A的响应曲线为三个测点的曲线包络线,港池B和C同理。针对本文港池尺度,入射波频率范围选为0.00125~0.025 Hz,高于该频率段的波浪,通常响应较小,并有明显的能量损耗,如底摩阻、涡动损失、边界部分反射等。低于该频率段的波浪,只会形成正常驻波。因此该频率段外的波浪不会造成严重的港湾振荡灾害。
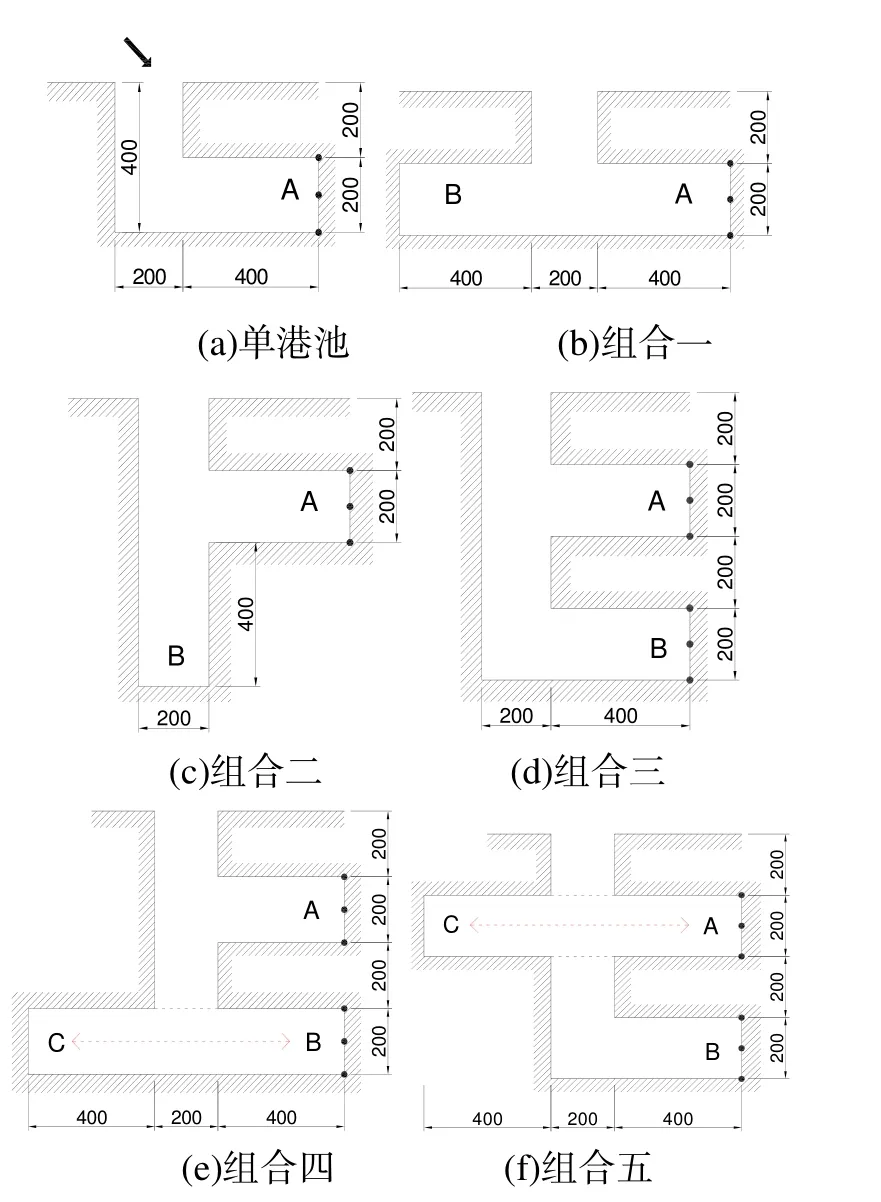
图2 港池布局示意(单位:m)
2.1 组合一
响应曲线对比见图3,各本征频率都用字母标记。本文将图中特别尖锐的峰称为极端模态,根据Bellotti[5]的研究结果,这类本征模态发展历时极长,可认为不具备实际的危险性。考虑前四个模态,组合一的本征频率要小于单港池情形。模式(b)在单港池情形为正常模态,在耦合情形转变为极端模态。模式(d)在耦合情形下更趋向于极端模态。在计算频率范围内,考虑到极端模态不具备实际的危险性,因此组合一的响应要弱于单港池情形。
为考察更全面的规律,此处另外取 0.025~0.1 Hz的频率段进行计算,结果见图3。两条曲线几乎没有任何相似规律可循,但对于个别极端模态,两个情形的本征频率是完全一样的,已在图中用蓝色直线标注出来。选择极端模态(1)和(2)的比波高分布见图 4,不难发现,这几个模态都属于沿着港池A宽度方向(y向)的极端模态,对应波节线数为1、3。极端模态(3)波节线数为4。由于频率分辨率不足,因此没有检索出波节线为2的模态。
综上所述,拓展港池B后,港池A沿长度方向(x向)的模态会发生改变,只有沿宽度方向(y向)的模态是不变的,但这些不变的又属于极端模态,实际意义不大。因此,只要拓展了港池,我们需要关心的模态都会发生变化。
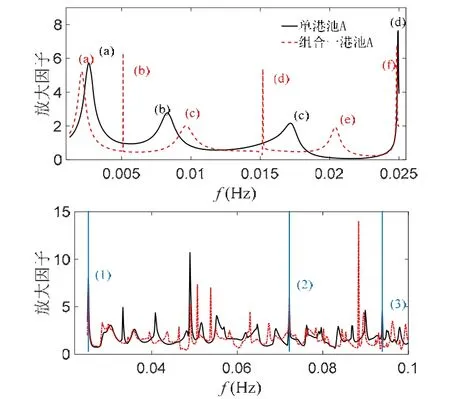
图3 组合一港池A响应曲线

图4 组合一中的极端模态
2.2 组合二
组合一和组合二可以看作港池B在不同位置的情形,对比图5,两者在低频区域(0.01 Hz之前)结果差异很小,本文认为是因为低频区域的波长较长。高频区域(0.02 Hz之后),共振峰有一定区别。对于模态(e),共振峰减弱了很多(组合二虽然很平缓但仍存在一个极点)。可以初步定性地认为,新建港池在不同位置的影响的区别主要体现在高频区域。
港池 A于组合一和组合二的平均放大因子分别为 0.89和0.95(表1),基本持平。结合外海波况考虑,如果能量主要集中在本征频率(d)附近,那么组合一更安全。若集中在本征频率(e)附近,则组合二更安全。若两者都不集中,那这两个组合情形没有明显区别,若将港池B的平均放大因子也考虑进来,此时组合一更安全(仅从内因考虑)。
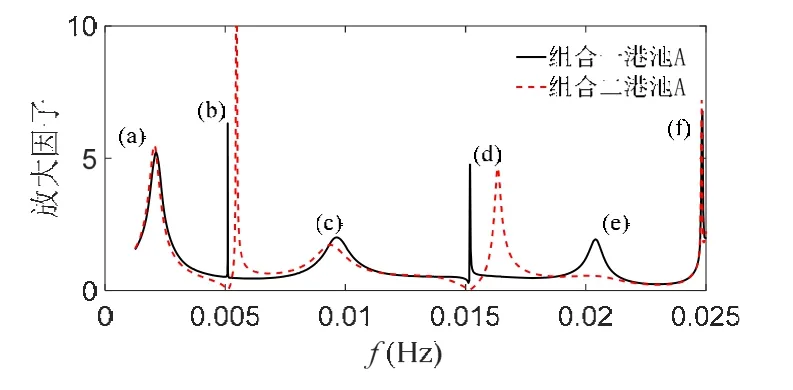
图5 组合二响应曲线
2.3 组合四&组合三
在组合三的基础上新增港池C,见图2(d)~(f),考虑港池C位置的不同对港池A和B的影响。观察港池A的响应曲线(图6),低频区域影响不大,只因为尺度增加而本征频率左偏,峰的形状改变了一点。港池A中第三个峰是往右移的,与设想的不一样。但同时观察港池B的响应曲线,第三个峰为极端模态,如果把港池A、B的曲线叠加的话,所有峰仍然是左移的,因此测点取的不够广泛便不能全面地反映所有的本征频率。
观察图6(b)中0.017~0.024(Hz)频率段,添加港池 C后,港池 B的响应提升了不少。组合四于0.02 Hz附近的共振峰的周期为50.04 s,在10 m水深下波长约为500 m,正好是BC向长度的一半,按一维封闭水槽理论,港池BC区域应有4根波节线,恰好与本文计算结果吻合(图7),即在这段频率,区域BC发生了明显的沿BC向的振荡(图2e红线所注),相当一部分能量在B港池和C港池之间循环。
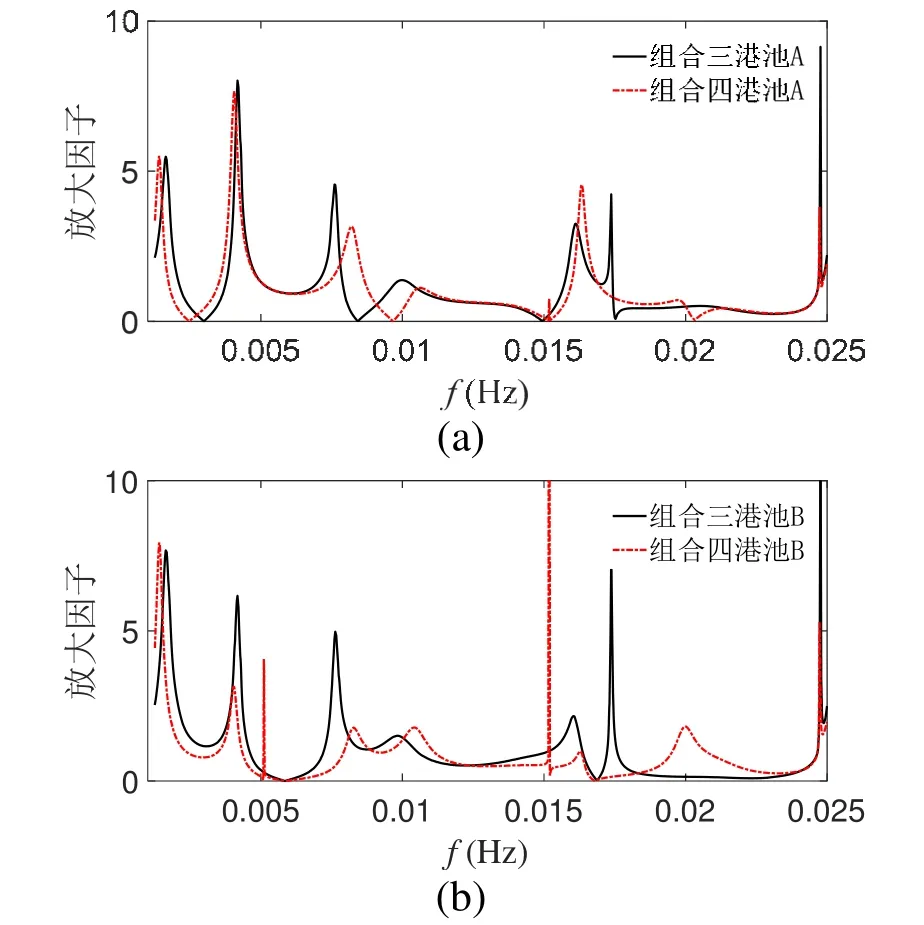
图6 组合四&组合三响应曲线对比
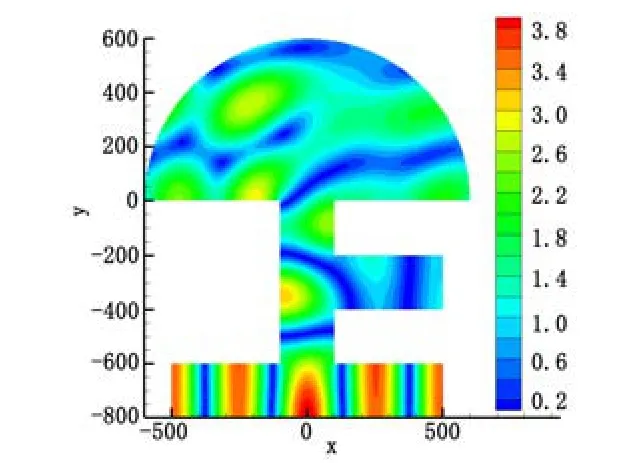
图7 组合四比波高分布(T=50.04 s)
2.4 组合五&组合三
此时港池A、B成正对着的联通港池,应有类似组合四中沿BC方向的振荡。观察港池A响应(图8),在 0.02~0.024 Hz频率段,组合五港池A的响应增强,但与组合四有两点不同,一是响应增强的程度较小,二是共振峰周期变为 45.46 s,波长为449 m,并不是很接近500 m(AC向长度的一半)。本文认为,这是因为组合四中区域BC与其他区域只有一条公共边界(图2e蓝色虚线所注),而组合五中区域AC与其他区域有两条公共边界(图2f蓝色虚线所注),对封闭性的影响更大。
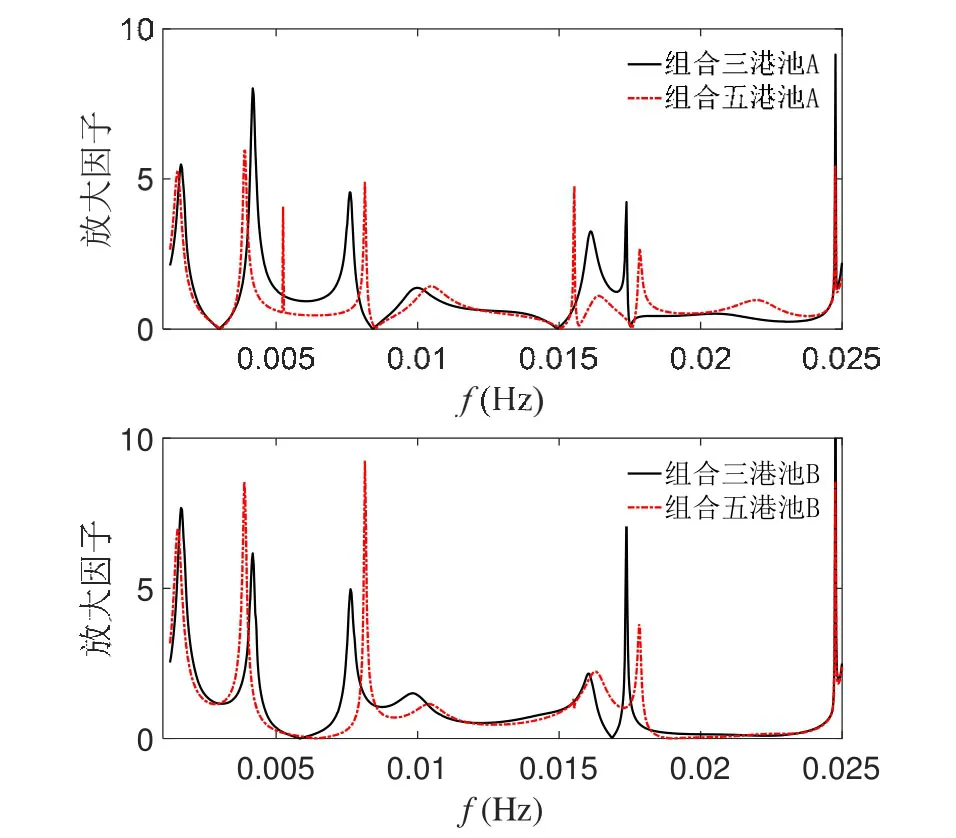
图8 组合五&组合三响应曲线
港池B(图8)中0.017~0.024 Hz频率段响应很弱,取周期为52.61 s情形进行计算,波浪斜向和正向入射下的比波高分布见图 9,几乎没有波浪进入当港池B。尝试使用开边界条件来判断哪条直墙的影响最大,选择4处作为开边界的组合(图10),没被选中则仍为全反射,各种组合及结果见图11。当开启港池B的直墙为开边界时,对结果几乎没有影响(图11a),说明波浪始终只有微小的一部分进入了B港池;当开启AC区域两端为开边界时,结果有了明显不同(图11c),说明恰巧是AC趋于两端的反射波造成特殊的波浪分布,只有少量波浪得以进入港池B。港口尺度会决定入射波从进入港口到经港内边壁反射离开港口的传播距离,当入射波波长与这一传播距离达到特定关系时,就会产生港口共振[2]。波向对弱响应频率结果的影响很小,可以把其看作港口共振的相反情形。只要入射波波长与港口尺度达到特定关系,港内局部区域的响应就会非常弱。
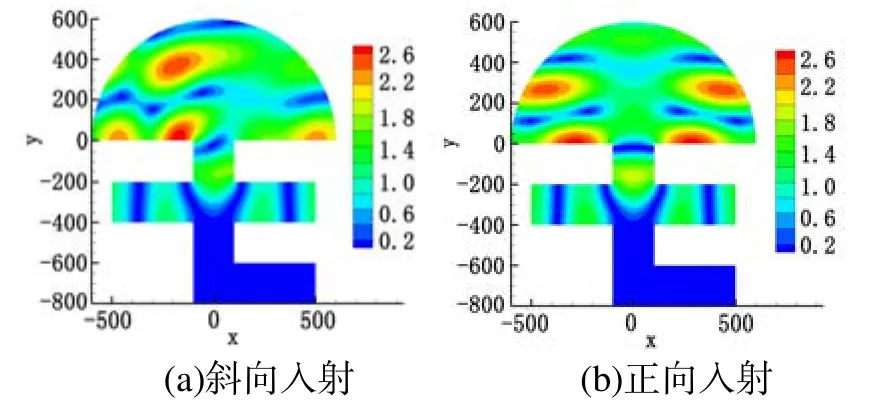
图9 弱响应频率相对波高分布(T=52.61 s)
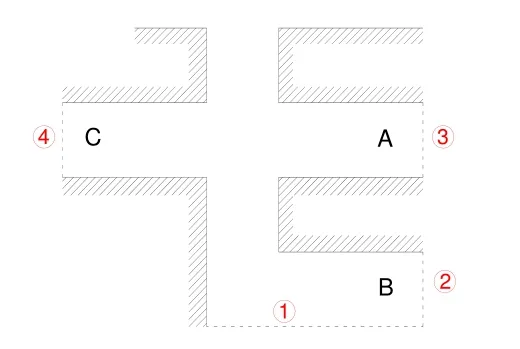
图10 组合五开边界位置示意
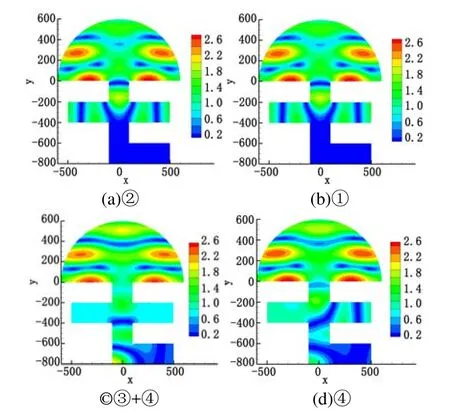
图11 不同开边界段的组合结果
组合四、五是基于组合三拓展的,从平均放大因子看(0),组合四、五都变得更小。只对比组合四、五,组合四的港池A响应强于港池B,组合五则相反。从内因上无法分辨哪个更安全,必须结合当地波况进行考虑。

表1 斜向入射下平均响应
3 总结
本文基于缓坡方程有限元模型研究了矩形港池组合的振荡特性,重点探讨了新建矩形港池后响应曲线和模态发生什么变化、港口会变得更安全或更危险等问题,简要总结如下:
1)基于组合一的结果,拓展港池后,响应曲线和振荡模态都会发生变化。拓展港池使得港口特征尺度变大,沿着主尺度振荡的模态的本征频率会变小(频域上往左偏移),正常模态可能会转变为极端模态,反之亦然。但有少部分极端模态不会受到影响,因为它们振荡方向的港池尺度没有发生改变;
2)当地波浪要素对评估港口共振危险程度有重要作用。由于极端模态不具备实际危险性,因此新增港池后,正常模态转化为极端模态,是有利的影响。反之,极端模态转化为正常模态,是不利的影响。响应曲线均值可以作为港湾振荡强度的内在指标,但想要合理地评估港湾振荡的实际危害,必须以加权形式考虑当地入射波浪波能的频率分布;
3)基于组合五和组合三的对比知,与港湾共振类似,弱响应频率(局部区域响应很弱)的出现也是因为入射波波长与港口尺度在数值上达到了特定关系。通过调整布局,使弱响应频率段与当地波要素相匹配,可以很好地改善港内泊稳条件。

