借助二次函数图像解不等式

文陶建燕

（作者单位：江苏省南京市江宁区铜井初级中学）

文陶建燕

我们知道，函数、方程、不等式之间存在联系，研究三者之间的联系绕不开对函数图像的研究，今天我们来“透过现象看本质”，借助函数图像解不等式。

例1已知：如图1，抛物线y=x2-2x-3。

（1）求该抛物线与x轴的交点A，B的坐标。

（2）x取何值时，y＞0？

图1

追问：结合图像，你能描述（1）（2）在函数图像中的意义吗？

【解析】（1）求二次函数的图像与x轴交点坐标，只需令y=0，将二次函数转化为一元二次方程x2-2x-3=0，求出方程的解x1=3，x2=-1，即交点坐标为A（-1，0），B（3，0）；或者将x轴看成直线y=0，只需求方程组的解即可。

（2）我们知道，只要令y＞0，即可将二次函数转化为不等式x2-2x-3＞0，可如何解这个不等式呢？目前我们没有研究过如何解这样的不等式，因此我们只有借助二次函数图像。从上下方向看，y＞0表示在x轴（直线y=0）上方的图像，从左右方向看，y＞0表示在交点A的左侧、交点B的右侧的图像。

为了直观地表示出应变量y＞0对应的图像，采用“划线分区”的方法，即分别过交点A、B作平行于y轴的直线，将图像分为三个区域：A点左侧，A、B两点之间，B点右侧。其中抛物线在x轴（直线y=0）上方的是A点左侧和B点右侧部分。这一方法是依据对应的函数图像和交点的位置关系产生的，因此应用时关键要找准交点再划线分区。

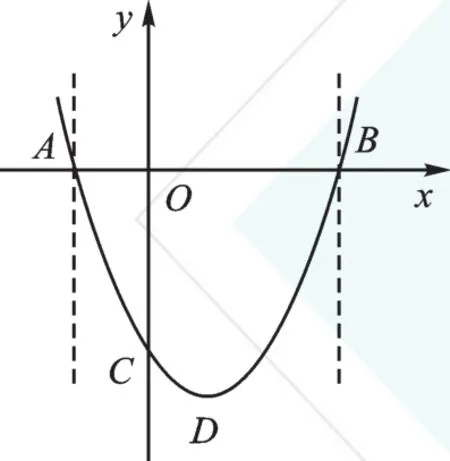
图2

由图2知，x的取值为x＜-1或x＞3。

【小结】“数形结合”最能展现二次函数与一元二次方程、不等式之间的关系：

数形y=x2-2x-3赋今y=0值今y=0 x2-2x-3=0 y=x2-2x-3赋 今y＞0值 今y＞0范 今y＞0围 今y＞0 x2-2x-3=0抛物线与直线的两个交点部分函数图像

理解了二次函数与一元二次方程、不等式之间的本质联系，掌握了“划线分区”的小妙法，你会解这一类不等式吗？我们来试试看。

变式1借助函数图像解不等式x2-2x-3≤-3。

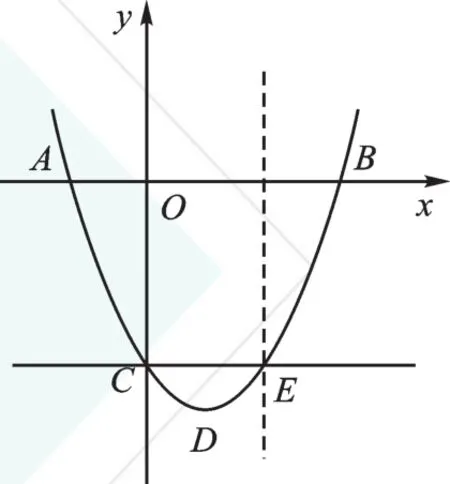
图3

【解析】不等式x2-2x-3≤-3表示y≤-3，结合函数图像，表示抛物线在直线y=-3下方的部分。在抛物线上画出直线y=-3，求出直线与抛物线的交点C（0，-3）、E（2，-3）。过交点C、E作y轴的平行线，把图像分成3个区域：交点C的左侧，C、E之间，交点E右侧。其中交点C、E之间的图像，表示y≤-3，即自变量x的取值范围是0≤x≤2。

变式2借助函数图像解不等式x2-2x-3＜x-5。

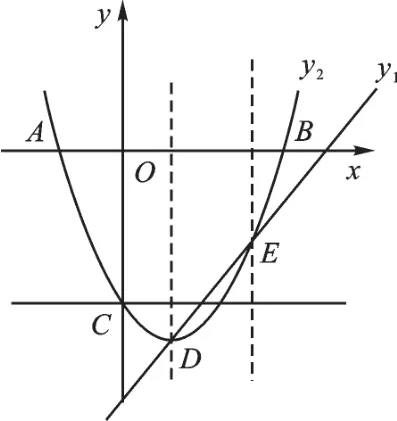
图4

【解析】不等式x2-2x-3＜x-5可看成抛物线y2=x2-2x-3与直线y1=x-5之间的不等关系，即y2＜y1。与变式1不同的是，平行于x轴的直线变为一般的直线，结合图像表示抛物线在直线的下方部分。同样用“划线分区”的方法解题。交点D、E之间的图像即为所求，自变量的取值范围为1＜x＜2。