两步渐进迭代逼近法和收敛性
刘仲云,李杰
(长沙理工大学 数学与统计学院,湖南 长沙,410114)
曲线拟合是计算几何中的基本问题[1],为了使曲线拟合给定的有序点集,文献[2]提出的标准曲线拟合方法通常需要求解线性系统[3]来计算其控制多边形的顶点,文献[4]指出,渐进迭代逼近法(PIA)和加权渐进迭代逼近法(WPIA),能避免求解线性方程的麻烦,同时具有清晰的几何意义和稳定的收敛性,引起了人们的关注。为了进一步丰富并得到收敛速度更快的渐进迭代逼近法,本文研究了文献[5-8]定义的Bernstein基的配置矩阵来拟合曲线的两步渐进迭代逼近法,进一步证明了两步渐进迭代逼近法是对加权渐进迭代逼近法的推广。数值实验表明,本文所得的两步渐进迭代逼近法具有更快的收敛速度。
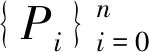
(1)
然后得到第一条初始拟合曲线
(2)
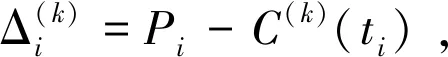
(3)

(4)
设λn(B)是配置矩阵B的最小特征值,加权因子ω=2/[1+λn(B)]加权渐进迭代逼近法比渐进迭代逼近法具有更快的收敛速度。
渐进迭代逼近法和加权渐进迭代逼近法都是对当前的控制多边形进行矫正。为了获得更好的方法,利用当前控制多边形和上一层控制多边形的控制点进行新的矫正,得到下面的矫正格式
(5)
其中:α,β为加速度参数。
显然,当α=1,β=ω时方程(5)就退化为加权渐进迭代逼近法。因此可以期望选取适当的α,β方法比(4)有更好的收敛性。
1 两步渐进迭代逼近法
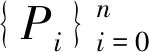
(6)
然后得到第一条初始拟合曲线
(7)
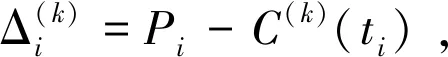
(8)
对应的残差向量为
(9)
其中:j=0,1,…,n,方程(9)对应的矩阵形式为
Δ(k+1)=(αI-βB)Δ(k)+(1-α)Δ(k-1)
(10)
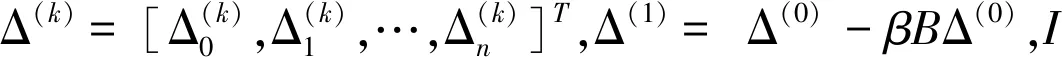
(11)
其中:k=0,1,…。

2 收敛性分析
本节讨论两步渐进迭代逼近法的收敛性,在给出收敛性之前先引入以下引理,见文献[3]。
1)λ0(B)=1, 0<λi(B)≤1,i=0,1,…,n;
2)0≤ρ(I-B)<1。
关于两步渐进迭代逼近法的收敛性,有如下定理。
1)两步渐进迭代逼近法收敛,当且仅当0<α<2, 0<β<2α;
2)H的谱半径ρ(H)有最小值当
其中:ρ0=[1-λn(B)]/[1+λn(B)]并且
证明:两步渐进迭代逼近法对于任何的初始控制点收敛,当且仅当ρ(H)<1,设(λ,x)是B对应的特征值与特征向量,即Bx=λx则有

对于每一个λ都存在两个对应的特征值μi(i=1,2)满足
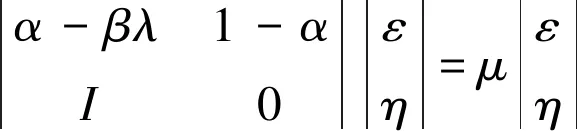
其中:[x,y]=[εx,ηx],ε=1,η∈,将上式化简得到μ2-(α-βλ)μ+(α-1)=0,从而|μ1μ2|=|α-1|<1, |μ1+μ2|<α, 所以0<α<2, 0<β<2α。
当maxλn(B)<λ≤1, |α-βλ|最小时特征值μ0=max{|μ1|,|μ2|}取最小值即
α-β=βλn(B)-α,β=2α/[1+λn(B)]
当v=(1-2λ)/[1+λn(B)]时得到α-βλ=αv,并且有
当λn(B)<λ≤1时有-ρ0≤v≤ρ0,定义函数
发现f′(α)≤0,并且
αopt是方程(αρ0)2-4(α-1)=0最小的根,即αopt=2/[1+(1-ρ02)1/2], 证毕。
对于加权渐进迭代逼近法,在文献[5]中选择最佳加权因子ω=2/[1+λnB], 从而有
推论3.1 对于任意的标准化全正基,两步渐进迭代逼近法比加权渐进迭代逼近法具有更快的收敛速度。
证明:定义函数
g′(x)=-2/(1+x)2<0对于任意的x∈(0,1)恒成立,根据引理3.1,有0<λn(B)<1,因此
从而,证明了两步渐进迭代逼近法比加权渐进迭代逼近法具有更快的收敛性。
3 数值实验
在本节中,选取了常用的具有代表性的例子,来验证两步渐进迭代逼近法的有效性。
例1 双扭线[x(t),y(t)]=[cos(t),sin(t)cos(t)],t∈[-π/2,3π/2]
例2 螺旋线[x(t),y(t),z(t)]=[5cos(t),5sin(t),t],t∈[0,6π]
在数值实验中,采用伯恩斯坦基来拟合双扭线与螺旋线,利用两步渐进迭代逼近法求相应的控制点。第k步迭代得到的曲线的拟合误差为
在以上两个例子中,考虑在文献[5]定义的Bernstein基的配置矩阵。 在表1中列出了参数ω,α,β的最佳值。在表2、3中分别列出了两种算法的计算结果,图1中给出了加权渐进迭代逼近法和两步渐进迭代逼近法的数值行为。
表1 双扭线、螺旋线对应的一些参数
Table 1 Certain parameters corresponding to twisted pair and helix

参数双扭线n=10n=20螺旋线n=18n=28ɷ1.999 32.000 02.000 02.000 0α1.800 01.800 01.900 01.900 0β0.300 00.300 00.300 00.300 0
表2 加权渐进迭代逼近法与两步渐进迭代逼近法求解例1的数值结果
Table 2 Numerical results of Case 1 by WPIA and TWPIA

n加权渐进迭代法ErrorITCPUtimes/s两步渐进迭代逼近法ErrorITCPUtimes/s109.866E-0713411.559E-027.778E-072339.814E-03209.975E-0713361.807E-029.442E-072351.199E-02
表3 加权渐进迭代逼近法与两步渐进迭代逼近法求解例2的数值结果
Table 3 Numerical results of Case 2 by WPIA and TWPIA
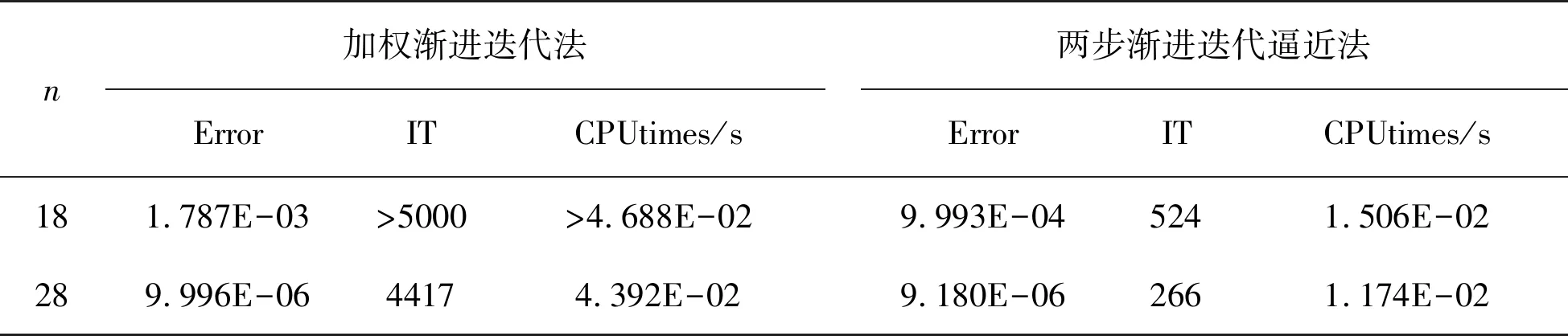
n加权渐进迭代法ErrorITCPUtimes/s两步渐进迭代逼近法ErrorITCPUtimes/s181.787E-03>5000>4.688E-029.993E-045241.506E-02289.996E-0644174.392E-029.180E-062661.174E-02
从表2、3和图1中可以看出,当达到相同的指定精度时,两步渐进迭代逼近法比加权渐进迭代逼近法有更快的收敛速度和更高的计算效率。
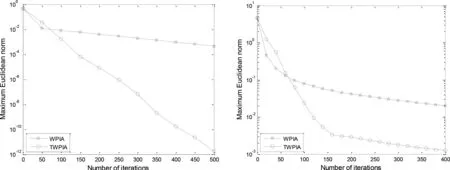
(a)双扭线,n=10 (b)螺旋线,n=18图1 加权渐进迭代逼近法与两步渐进迭代逼近法收敛性行为Fig.1 Convergence behaviors of WPIA and TWPIA

