相对Gorenstein 投射复形

何东林,李煜彦

(陇南师范高等专科学校 数信学院,甘肃 陇南,742500)

Gorenstein 同调理论是相对同调代数的重要内容。1969年AUSLANDER和BRIDGER在文献[1]中讨论了双边Noether环上有限生成模的G-维数。1995年ENOCHS和JENDA在文献[2]中给出任意环上Gorenstein投射模的概念。Gorenstein投射模有许多与投射模类似的性质，参考文献[3-7]对其进行了推广。特别地，BENNIS等[3]给出了X-Gorenstein 投射模的概念和若干性质。孟凡云等[8]对这一概念做了进一步研究。复形和复形每个层次上模的关系的研究是一个重要课题。ENOCHS和GARCIA[9-10]证明在Gorenstein环R上,复形X是Gorenstein投射复形当且仅当模Xm是Gorenstein投射模(对任意m∈Z)。杨刚[11]研究了一般结合环上复形的Gorenstein 投射性。自然而然地，可考虑相对于某个左R-模类C的Gorenstein投射复形，以及复形的C-Gorenstein投射性与其每个层次上的模的C-Gorenstein投射性之间的关系。进而研究C-Gorenstein复形的性质和等价刻画。

文中的环R均指有单位元的结合环，模指酉模。X表示一个关于直和封闭且包含所有投射模的左R-模类。左R-模复形…→X-1→X0→X1→X2→…记为X，用Y表示左R-模复形组成的Abel范畴。显然，该范畴有足够的投射对象和内射对象。对任意复形C和D，用Hom(C,D)表示C到D的同态群，Exti(C,D)表示由Hom(C,D)导出的第i个同调群，C#表示形如C≡…→C-1→C0→C1→C2→…(其中Ci∈C)的正合复形组成的类。

1 定义和引理

C-Gorenstein 投射模的概念。

定义1[8]称左R-模M是C-Gorenstein 投射模，如果存在正合列

…→P-2→P-1→P0→P1→…

(1)

其中：Pi为投射模，M=Ker(P0→P1)且对任意H∈C有正合列(δ)在函子HomR(-,H)仍正合。用CGP表示所有C-Gorenstein 投射模组成的类。

下面引入C-Gorenstein 投射复形。

定义2 称左R-模复形X是C-Gorenstein 投射复形,如果存在复形正合列

…→P-2→P-1→P0→P1→…

(2)

其中：Pi为投射复形，X=Ker(P0→P1)且对任意复形C∈C#，该正合列在HomR(-,C)下仍正合。

易知：1)投射模⟹ C-Gorenstein 投射模⟹ Gorenstein投射模。

2)投射复形⟹C-Gorenstein 投射复形⟹Gorenstein投射复形。

引理1 设X为左R-模复形，则C是C-Gorenstein 投射复形当且仅当存在复形正合列

…→P-2→P-1→P0→P1→…

(3)

满足以下条件：1)Pi为投射复形；2)X=Ker(P0→P1)；3)对任意复形C∈C#和任意Ii=Im(Pi-1→Pi)，都有Ext1(Ii,C)=0。

证明由Ext函子的定义和性质易证。

引理2[8]设0→M→N→L→0是左R-模正合列，其中N,L是C-Gorenstein投射模。如果对任意投射模Q有Ext1(M,Q)=0，那么M也是C-Gorenstein投射模。

2 主要结论

命题1 设k为正整数，X为左R-模复形。如果对任意复形C∈C#，有Extk(X,C)=0，那么对任意N∈C，有Extk(Xm,C)=0。

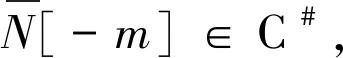
(4)

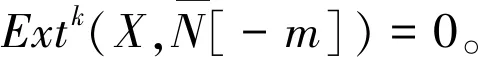
0→N→E0→E1→…→Ek-1→L→0

(5)

其中：Ei为内射模。令H=Im(Ek-2→Ek-1)，则有正合列0→H→Ek-1→L→0和0→N→E0→E1→…→Ek-2→H→0。由维数转移公式可得

Ext1(Xm,H)≅Extk(Xm,N)

(6)

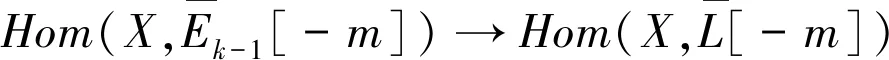
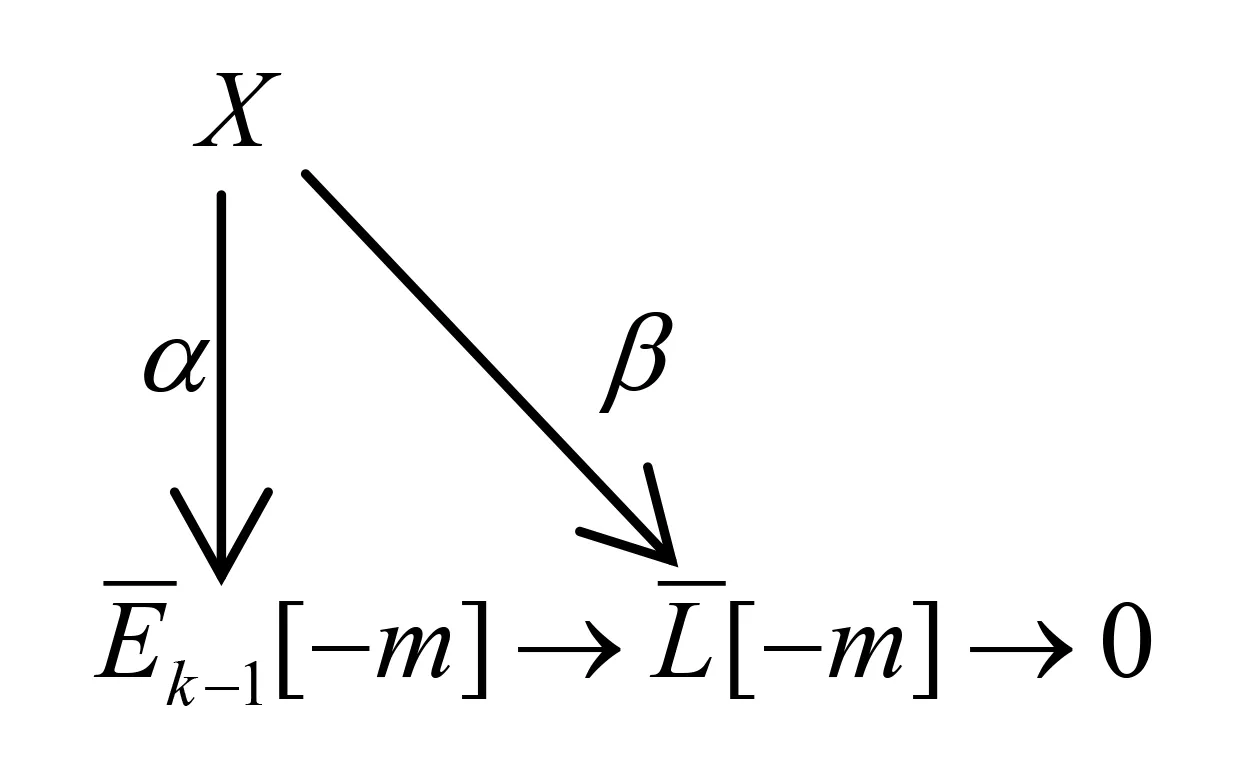
图1 复形的交换图Fig.1 The commutative diagram of complex

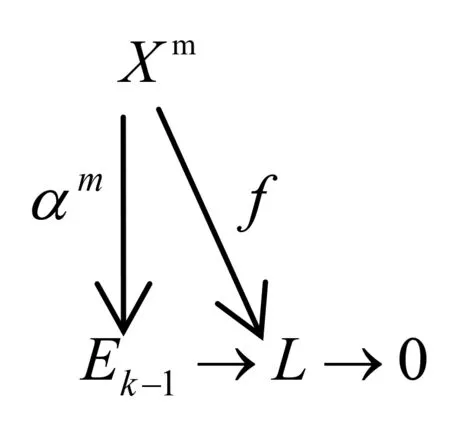
图2 图1的第m个层次图Fig.2 The mth term diagram of Fig.1

因此Hom(Xm,Ek-1)→Hom(Xm,L)→0正合，另一方面有正合列

Hom(Xm,Ek-1)→Hom(Xm,L)→Ext1(Xm,H)→0

可见Ext1(Xm,H)=0，又因为Ext1(Xm,H)≅Extk(Xm,N)，所以Extk(Xm,N)=0。

推论1 设X为左R-模复形。如果对任意复形C∈C#，有Ext1(X,C)=0，那么对任意N∈C，有Ext1(Xm,N)=0。

推论2 如果X是C-Gorenstein投射复形，那么每个层次上的模Xm是C-Gorenstein 投射模。

证明 设X是C-Gorenstein投射复形，则由引理1知存在复形正合列

…→P-2→P-1→P0→P1→…

(7)

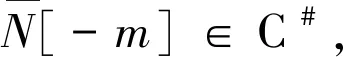
(8)

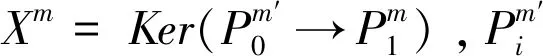
命题2 设M是C-Gorenstein投射模，则对C中任意模N的每个上合冲I有

Exti(M,I)=0。

证明 设N∈C，且N的第n个上合冲为I。则存在正合列

0→N→E0→E1→…→En-1→I→0

(9)

其中：Ej为内射模且Exti(M,I)≅Exti+n(M,N)。因为M是C-Gorenstein投射模且N∈C，所以Exti+n(M,N)=0，所以Exti(M,I)=0。

定理1 设X为左R-模复形，则以下条件等价

1)X是C-Gorenstein投射复形；

2)每个层次上的模Xm是C-Gorenstein 投射模。

证明 (1)⟹(2)由推论2易证。下证(2)⟹(1)对任意M∈C，考虑正合列

0→M→E0→E1→…→En-1→I→0，

(10)

其中：Ej为内射模。令I0=Im(M→E0)，In=Im(En-1→I)且Ij=Im(Ej-1→Ej)，其中j=1，2,…,n-1。那么对每个整数m，复形序列

(11)

(12)

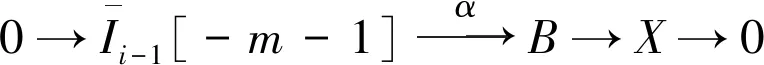
图3复形正合列展开图
Fig.3The expanded graph of complex exact sequence

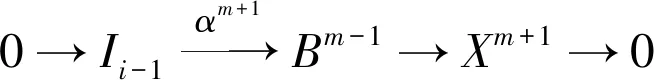
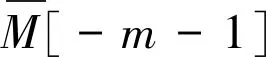
因为每个层次上的模Xm是C-Gorenstein 投射模，所以Xm是Gorenstein 投射模。显然Xm具有投射预包络。由文献[11]中引理2可知复形X具有投射预包络。不妨设γ0：X→P0是X的投射预包络。易知γ为单同态。考虑正合列0→X→P0→H1→0，其中H1=Cokerγ0。由于γ0是X的投射预包络。且对任意C∈C#有正合列

0→Hom(H1,C)→Hom(P0,C)→Hom(C,C)→Ext1(H1,C)→Ext1(P0,C)=0

(13)

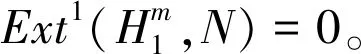
0→X→P0→P1→P2→…

(14)

其中：Pi为投射复形，且对任意复形C∈C#正合列(1)在HomR(-,C)仍正合。

考虑由投射覆盖导出的如下复形正合列

…→P-3→P-2→P-1→X→0

(15)

因为对任意i≥1和任意复形C∈C#，有Exti(X,C)=0。所以(2)在HomR(-,C)正合由(1)(2)拼接可得复形正合列

…→P-2→P-1→P0→P1→…，

其中：Pi为投射复形，X=Ker(P0→P1)且对任意复形C∈C#有正合列(ε)在HomR(-,C)下仍正合。因此X是C-Gorenstein投射复形。

推论3 X-Gorenstein投射复形关于扩张和满同态的核封闭。

证明 由定理1和文献[3]中易知。