基于谱峭度的同步提取变换方法及故障诊断应用

张 浩，张 坤，田伟康，胥永刚

（北京工业大学先进制造技术北京市重点实验室，北京 100124）

0 引言

旋转机械广泛地应用于机电设备中，而在多数旋转机械中滚动轴承起到至关重要的作用，被人们称为机器的关节[1]。伴随着我国科技水平的提升，在实际工况中常伴随着高温差、高压力差、强噪声等恶劣环境，在这种工况下滚动轴承很容易造成损伤并且很难保持平稳的工作状态，极易发生轻微损伤并且较难精准确定损伤部位[2]。因此采集轴承的振动信号监测其状态并诊断故障具有非常重要的工程应用价值[3]。同步提取变换（Synchroextracting transform，SET）通过提取短时傅里叶变换（Short-time Fourier transform，STFT）在瞬时频率位置的时频系数可获得较理想的时频谱。该方法一方面提高了时频分辨率，另一方面亦减少了交叉项的影响，一定程度上抑制了噪声对STFT 时频谱的干扰，然而在SET 时频谱的基础上进行自适应故障诊断拓展应用方面尚待进一步研究。

在时频分析方法中，短时傅里叶变换、Wigner-Ville[4]时频分布、小波分析、离散小波变换、双树复小波变换以及近年来提出的基于自适应分解理念的同步压缩变换（Synchrosqueezing transform，SST）等方法[5-6]。S.Vulli 针对发动机的振动研究中，利用STFT 得到信号的二维时频谱，并成功识别出了发动机正常工况下的爆燃激励及各种故障特征[7]。Yang Jin 比较了STFT 与其他时频分析方法的特点与优劣，并利用发动机振动信号验证了各种时频方法适用范围。J Antoni 发现信号中的非平稳分量，在时频谱中本身的特征频率附近具有较大的峭度值，通过计算STFT 谱中各频点的峭度特征，有效提取到信号中的非平稳分量[8-9]。

基于时频变换分辨率不高的问题，于刚[10]在STFT 的基础上提出一种新的时频分析方法SET。该方法在STFT 的基础上用两个窗函数对信号进行傅里叶变换，然后对得到的两个新的一维信号对比分析，通过阈值对数据进行筛检，最后得到一组新的数据，也就是同步提取变换后的信号。同步提取变换具有时频分辨率高，可用于模态分解、弱信号检测、S 变换等方法和实时计算。但该文献中并未继续深入研究信号的自适应提取问题。自适应获取信号分量有利于进一步诊断故障，将SET 理论向实用方向拓展。

提出了一种基于谱峭度的自适应信号处理方法，利用峭度值对周期性冲击信号的敏感性，将谱峭度与SET 相结合，可以快速、准确地判断故障特征频率的位置及自适应的提取特征频率，再对提取的分量进行包络分析，成功提取了滚动轴承的故障特征信息。

1 同步提取变换基本原理

同步提取变换（SET）[7]提取瞬时频率的时频系数，所携带的噪声大大减少，鲁棒性得到增强。其步骤分为以下3 步：①根据STFT 计算时频谱；②根据相位信息估计瞬时频率；③提取STFT在瞬时频率位置的时频系数。

该方法首先需要根据STFT 计算信号s（t）的时频谱：

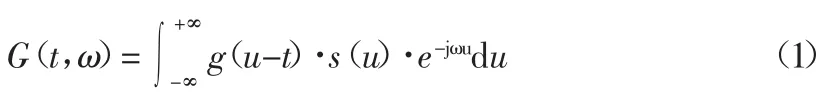
对式（1）乘以相位因子ejωt：

式（2）表示该方法在保证窗函数不变的前提下移动信号进行FFT 计算。根据文献［10］此处选取的窗函数为高斯窗，窗函数越短，时间分辨率越高，窗函数越长，频率分辨率越高。为了保证时频图的时频聚集性，窗宽的选择应该适中。具体的窗宽选择应根据数据的长度进行确定。中设频率为ω0的谐波信号s（t）=A·ejω0t，其频域表示为：

将式（3）代入式（2），则时频谱可表示为：

式（4）说明，一系列与谐波信号频率一致的时频系数组成谐波信号的STFT 谱。由于窗函数在频域紧支且在0 频率处有最大值，因此在时频谱中频率ω=ω0处的时频系数幅值最大，为。此时距离ω0越远的时频系数幅值越小。可采用式（5）估计STFT 谱中时频系数的瞬时频率。

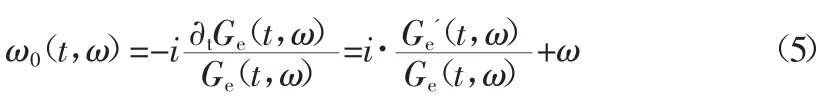
其中，∂tGe（t，ω）是Ge（t，ω）对时间的一阶偏导数。由此在二维时频平面中，可以得到一个与STFT 谱系数一一对应的新的时频谱ω0（t，ω）。

仅提取STFT 谱在瞬时频率位置的时频系数，对应公式可表示为：

其中，δ（ω-ω0（t，ω））称为同步提取算子。

同步抽取变换的逆变换如式（7）所示：

文献［10］将信号的重构问题近似为STFT 谱的脊提取问题，但其重构方法为简单的数据叠加处理。本文进一步研究了信号分量的分解与重构，利用顺序统计滤波器对信号的边际谱进行频带划分，将时频谱中不同的信号分量分割开来分别重构，并拓展应用于滚动轴承故障诊断中。

同步提取变换重构如式（8）所示：

2 改进快速谱峭度

同步提取变换信号重构步骤：

快速谱峭度图需要构建滤波器进行滤波处理，但是同步提取变换本身带有滤波效果，不需要再次进行滤波处理。基于同步提取变换的改进快速谱峭度图算法的流程如下：

（1）对信号进行同步提取变换。

（2）在时频图上对SET 处理后的信号进行连续层数划分。

（3）对划分好的数据进行重构。

（4）对重构后的信号求取峭度值，得到改进后的峭度图（图1）。

图1 改进快速谱峭度

3 仿真信号分析

为了验证修改方法的可行，构建一个仿真信号x（t）如式（9）所示。

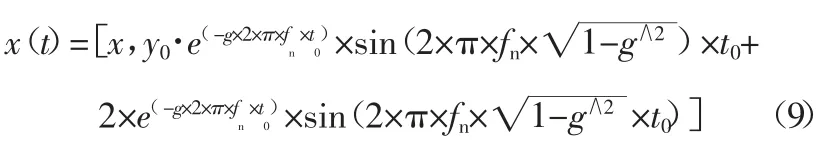
其中，fn为固有频率，t0为单周期采样时刻，g 为阻尼系数，y0为位移常数。

对该仿真信号添加噪声，信噪比为-1 dB。叠加后的信号的时域波形如图2 所示，

图2 加噪信号波形

通过同步提取变换对信号s（t）进行处理，然后求得峭度值，最后得到峭度图（图3）。

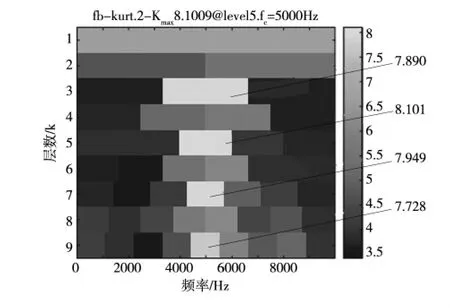
图3 SET 改进峭度

从峭度图中得到，峭度值最大位于第五层第三部分。这部分峭度值最大说明该频段内的信号冲击最为明显，因此对该部分进行提取并作进一步分析。

在这里确定了峭度图上最大峭度的位置，然后利用改进同步提取变换方法，对峭度最大处进行信号提取（图4）。

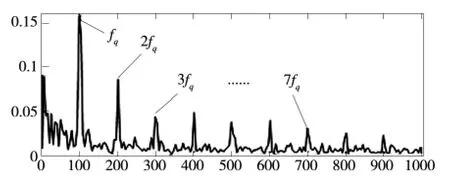
图4 包络分析

从图4 中可以找到特征频率及其倍频，验证了本方法的正确性。

4 实验信号分析

取型号6307 滚动轴承并预置外圈故障，测取其振动信号。电机转速为1496 r/min，采样频率7100 Hz。计算求得该轴承内圈转频为24.93 Hz，外圈故障特征频率为77.3 Hz，信号的波形如图5 所示。

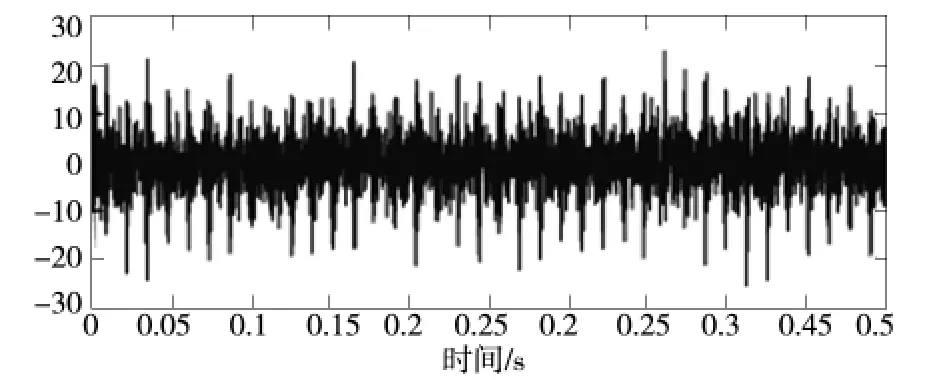
图5 原始信号波形

对信号进行同步提取变换处理，求峭度值，最后得到峭度图（图6）。

图6 改进峭度

从峭度图中得到，最大的峭度值位于第五层第三部分。表明该部分的周期性信息最为明显，因此可以对其进行故障信息的提取分析。

通过对峭度图上最大峭度位置的识别，利用改进同步提取变换方法，对峭度最大处进行信号提取（图7）。

图7 信号提取示意

对提取的信号进行包络分析，得到包络图（图8）。

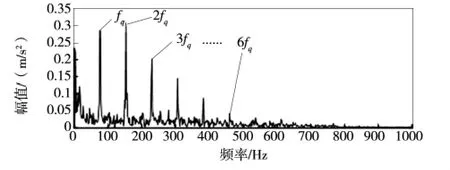
图8 包络分析

从图8 中可以找到该轴承外圈故障特征频率及其倍频，由此可以判断该轴承外圈出现故障。验证了本方法的正确性。

5 结语

（1）提出了一种基于谱峭度的同步提取变换方法，实现了信号的自适应分解，可提取滚动轴承振动信号中的周期性冲击分量。

（2）仿真信号和实验信号验证了该方法的可行性。

（3）将基于谱峭度的同步提取变换方法应用于滚动轴承故障诊断，可以有效地提取故障信息。