初中数学教学中“旋转变换”模型解题策略研究
李淑琴


摘 要 初中几何教学中,为了提高教学质量,让学生学会快速解题方法,可考虑采用模型教学的方式,在很大程度上降低了解题的难度,激发了学生的学习兴趣,也使得教学效果得到了显著的提高。因此,模型教学在初中数学几何教学中起着很重要的作用,本文中笔者对“旋转变换”模型解压轴题进行了探究,在教学中,结合实例,渗透数学建模思想,寻找“旋转变换”模型,获得较好的教学策略时,也提高了学生的学习兴趣,帮助学生解决中考压轴题问题。
关键词 初中数学 几何模型 旋转变换
中图分类号:G633.6文献标识码:A
在初中数学几何中运用模型教学,在一定程度上促进了教学质量的提高。“旋转变换”特性的应用,是新课改背景下必然的产物,对初中阶段的几何数学有重大的影响。作者借助多年的教学体会,结合实例,对初中数学中几何模型的教学进行了探讨和分析。
1初中几何中常见的应用模型之一——旋转变换模型
1.1教师在教学中的参与与引导
在中考中,应用“旋转变换”解压轴题已成为学生必备的一种几何解题技巧。教学中要求学生掌握作图的操作技能,还要认识旋转的形成过程及旋转变换发生的关键——找到一组边相等,使旋转前后这两边能够完全重合,这样就可以对原图形或某线段进行变换,培养学生的发散思维。
1.2结合实例
1.2.1对角互补型——90?
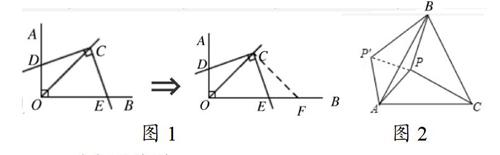
如上图1,四边形中,若相对两个角的和为180啊T蚩梢酝DO,构造三角形全等或相似。
1.2.2通过旋转构造直角三角形
例题:如图2,P是等边△ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转60昂螅玫健鱌′AB。
(1)△APP′的形状是;(2)求∠APB的度数。
解:(1)∵将△PAC绕点A逆时针旋转60昂螅玫健鱌′AB,这样就证明△APP′为等边三角形;(2)∵△APP′为等边三角形,∴PP′=AP=6,∠APP′=60埃?
∵将△PAC绕点A逆时针旋转60昂螅玫健鱌′AB,
∴P′B=PC=10,
在△PBP′中,BP′=10,BP=8,PP′=6,∵62+82=102,∴PP′2+BP2=BP′2,∴△BPP′为直角三角形,∠BPP′=90埃唷螦PB=∠APP′+∠BPP′=60?90?150啊?
点评:此题关键就是利用旋转特性作出辅助线构造全等是解答本题的关键。
1.2.3截長补短型
截长:(1)过某一点作长边的垂线;(2)在长边上截取一条与某一短边相同的线段,再证剩下的线段与另一短边相等。
补短:(1)延长短边;(2)通过旋转等方式使两短边拼合到一起。
如图,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45,求证:EF=BE+DF。
分析:如图,通过旋转把△ABE旋转到△ADG,则△ABE≌△AFG进而得到BE+DF =FG,再证AFE≌△AFG问题即可解决。
2“旋转变换”模型在数学几何教学中应用的建议
初中生正处于发育阶段,其思考学习的能力还不健全,而想要掌握和应用初中数学的几何知识,需要具备一定的逻辑思维能力。几何题讲解中,充分挖掘图形中的基础图形和基本模型,引导学生在学习的过程中自主思考,把握变换的规律,解决问题。教师在教学过程中,把熟悉的模型直观地展现在学生面前,让学生观察、发现不同的几何图形之间存在的共性与差异性,而学生在在参与寻找与发现的过程中,获得成功的体验,并感受到数学几何带给自己的快乐,从而有助于激起学生学习数学几何知识的兴趣和爱好。而老师在教学过程中,通过模型展现给学生一些不容易表达的抽象的知识,学生容易听懂,教师也省掉了很多不必要的麻烦,还有利于学生逻辑思维能力的提升,进而促进数学整体水平的提升。
综上所述,几何知识是初中数学教学中的一大难点,面对抽象的知识,教师和学生都有很大的挑战性。对于旋转变换的解题策略仍不断的进行研究,利用旋转变换进行复杂问题简单化也将成为学生解题的工具之一。相信在教师的引导下,学生一定会将旋转变换内容理解、熟透并应用它进行解题。
参考文献
[1] 李守霞.初中数学几何教学中运用模型教学研究[J].中国校外教育:中旬,2015.
[2] 徐波.巧用辅助线,构造三角形全等解决问题的策略[J].数理化解题研究:初中版,2014(04).
[3] 刘雪琴.以三角板为载体的动手操作型问题[J].上海中学数学,2006(12).
[4] 马艳凤.浅谈信息技术与数学课的整合在教学中的作用[J].新课程导学(九年级下旬),2009.

