融合稀疏隐视角信息学习的多视角聚类算法*

刘瑞秀，高艳丽，邓赵红+，王士同

1.江南大学 数字媒体学院，江苏 无锡 214122

2.江南计算技术研究所，江苏 无锡 214083

1 引言

聚类是一种基于相似性信息，将对象或数据样本划分为若干组或类的方法。聚类是一种无监督学习技术，它作为一种重要的数据处理方法，在数据挖掘、图像处理、模式识别等领域有着广泛的应用。传统的聚类分析方法主要有K-means[1-3]、FCM（fuzzy C-means）[4-6]、MEC（maximum entropy clustering algorithm）[7-8]、PCM（possibilistic C-means algorithm）[9-10]、谱聚类[11-12]等。这些方法具有计算简单、速度快等特点，并且有着广泛的应用领域。但是，随着现代技术的发展，所采集数据的大小、属性等越来越复杂。许多数据集都可以用不同的属性集描述，即多视角数据。例如一个文档可以被翻译成英语、汉语两种语言；一个网页可以用两个视角描述，一个是网页上出现的文本，另一个是指向该网页的超链接上的文本。不同的视角之间通常提供兼容和互补的信息。由于传统的聚类分析方法只使用数据样本的一个特征集或一个视角，其在处理多视角数据集时，不能充分利用视角与视角间的关联性。因此，如何从多视角数据中整合信息，以获得更好的聚类性能已成为机器学习中的一个重要的课题。

近年来，为了提高多视角聚类算法的性能，已经开发了许多多视角聚类方法。文献[13]基于期望最大化提出了协同聚类算法Co-EM（collaborative expectationmaximization algorithm）算法；同样基于协同的思想，文献[14]提出了一种双视角谱聚类的算法。文献[15]提出了多视角谱聚类算法，这些都是早期基于协同思想的多视角聚类算法。基于经典的K-means算法，文献[16]提出了双层变量自动加权聚类算法TW-Kmeans。通过在经典的模糊C-均值（FCM）中引入协同的思想，文献[17]提出了一种协同聚类算法Co-FC（collaborative fuzzy clustering）算法。文献[18]基于FCM算法提出多视角模糊聚类算法Co-FKM（collaborative fuzzyK-means），该算法通过在目标函数中引入一个惩罚项，减少了不同视角之间划分的不一致性。文献[19]以经典的FCM 算法为框架，提出了多视角模糊聚类Co-FCM算法，然后为了识别每个视角的重要性程度，文献[19]基于香农熵又提出了其增强版本多视角加权协同模糊聚类算法WV-Co-FCM。文献[20]在经典的FCM 算法中引入了最小最大优化项，提出了多视角模糊聚类算法MinimaxFCM。

另一方面，一些文献提出通过不同的方法将多视角数据从不同的特征空间转换到一个共同的低维特征空间。这个低维空间的数据就是嵌入在多视角数据的隐性信息。例如文献[21]提出了一种基于联合非负矩阵分解的多视角聚类算法，该算法首先通过联合非负矩阵分解方法将从每个视角学习的系数矩阵规范化成一个共同的一致性矩阵，然后直接应用K-means或其他聚类算法对一致性矩阵聚类。文献[22]基于核典范相关分析提出了相关谱聚类算法，该算法首先将多视角数据从多个特征空间映射到一个共同的低维子空间，然后应用K-means等聚类算法对低维空间的数据进行聚类。文献[23]基于无向潜在的空间马尔可夫网络，通过提出一个通用的大边缘学习框架来发现由多个视角共享的预测潜在子空间表示。

尽管上述文献提出的多视角聚类方法为解决多视角聚类问题提出了可行的方案，并且也都取得了很好的聚类性能，但是有两个主要的缺点。第一，一些多视角聚类算法[16-19]主要运用多视角数据集的原始特征聚类，而没有深入挖掘各视角间存在的隐性信息，这些隐性信息往往对聚类效果起重要的作用。第二，一些多视角聚类算法[21-23]试图发现嵌入在多视角数据中的隐性信息并基于隐性信息进行聚类，但此类算法会不同程度地丢失原始特征的信息。这是由于原始的各视角数据更多地反映了个性化信息，仅用隐性信息会过多地偏重于共性信息，而对个性化信息没能有效使用。多视角学习的关键是如何综合利用各视角间个性化信息和共性信息。在多视角聚类中，如何将个性化信息和共性信息有效融合起来，是一个具有挑战性的课题。

针对上述挑战，本文提出了融合稀疏隐视角信息学习的多视角聚类算法。该算法首先通过求解一个多视角稀疏隐信息学习模型得到多视角数据共享的稀疏表示系数矩阵，即隐性信息。该隐性信息在一定程度上描述了不同数据点之间的共性信息，并且具有稀疏性。然后，采用协同学习的方式同时对原始特征集和隐性信息聚类，同时引入香农熵策略自适应地调整不同原视角的权重。将上述策略应用到经典的FCM 聚类框架，得到融合稀疏隐视角信息学习的多视角聚类算法。

2 相关工作

2.1 多视角聚类

传统的单视角聚类算法处理多视角数据的框架如图1所示。在处理多视角数据时，传统的聚类方法通常独立地考虑每个视角，并将每个视角视为独立的聚类任务，分别对每个视角进行聚类获得每个视角下的划分矩阵，然后使用简单加权或集成学习机制[24-25]获得全局的划分矩阵。这种方式虽然为单视角算法处理多视角数据提供了一种可行的方法，但是简单地进行加权整合没有考虑到视角与视角间的关联性，这在一定程度上会造成聚类效果不佳。与此不同的是，多视角聚类充分利用来自不同视角的信息，通过运用不同视角之间的相关性和协作来训练模型。现有的多视角聚类算法大致可以分为三类。第一类算法在聚类过程中实现视角间的协同学习[16-20]。第二类算法试图发现嵌入在多视角数据中共同低维子空间的表示，然后再用某种单视角聚类算法对这个数据进行聚类[21-23]。第三类就是后期融合[26-27]，也就是分别处理每个视角的数据，最终的聚类结果来自每个单独的视角聚类结果的整合。例如文献[26]通过引入映射函数，使得来自不同视角的集群具有可比性，同时从多个视角的多个集群中学习最佳的集群；文献[27]基于在单个数据集上计算不同的相似矩阵，并且聚合形成组合相似度矩阵，然后将其用于获得最终聚类结果。

Fig.1 Classical framework of single view clustering algorithms for multi-view data图1 经典的单视角聚类算法处理多视角的框架

2.2 稀疏表示

近年来，稀疏表示[28-29]（sparse representation，SR）在模式识别、图像处理等研究领域受到了广泛的关注和研究，其目的就是在给定的字典中，用尽可能少的原子的线性组合来表示数据，由此获取数据样本之间的联系。最简单的稀疏表示模型是：

其中，||c||0是l0范数，用来计算c中非零元素的个数；y∈Rd是数据样本，D∈Rd×K是字典矩阵，x∈RK是系数向量。由于式（1）是NP难问题，因此通常用l1范数来代替l0范数。字典的选取是至关重要的，许多稀疏表示模型都用数据集本身作为字典，即稀疏自表示。许多算法都采用数据集本身作为字典，例如文献[28]使用数据集本身作为字典，提出了一种稀疏子空间聚类算法（sparse subspace clustering，SSC）；文献[29]提出了一种低秩表示的子空间聚类方法（low rank representation，LRR）。通过SSC、LRR 等算法得到的稀疏表示系数矩阵能很好地反映数据集的潜在的群结构信息，并且具有稀疏性，从中能够很好地发现数据样本间的关系。这促使把稀疏表示方法应用到多视角聚类中。

3 融合稀疏隐视角信息学习的多视角聚类

3.1 多视角稀疏隐信息抽取

给定一个多视角数据集X={X(1)X(2),…,X(K)}，共K个视角，第k个视角的样本集用矩阵表示为，1 ≤k≤K。其中N表示样本个数，dk表示第k个视角的特征数。通过解决如下优化问题得到多视角数据的稀疏隐视角信息：

其中，Z∈RN×N是多视角数据共享的稀疏表示系数矩阵，即隐视角。||.||F是Frobenius范数，||.||1是l1范数，diag(Z) 是隐视角Z的对角线元素，并且约束条件diag(Z)=0可避免平凡解，即避免每个样本用自身表示。

在式（2）中，每一项的描述如下：

（2）第二项||Z||1是l1正则化项，该项的目的是使隐视角尽可能地稀疏。

（3）第三项是流形正则化项，该项是为了维持每个视角中的原始特征的流形结构。对于第k个视角，如果两个数据点在原始的特征空间中彼此接近，那么在隐视角中，这两个数据点也应该是彼此接近。第k个视角的相似度矩阵为S(k)，让，则有：

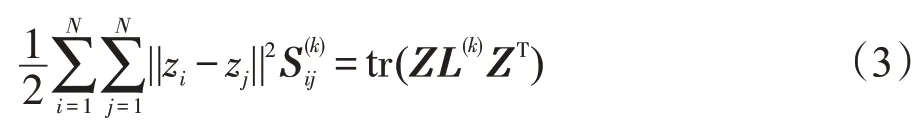
其中，L(k)=D(k)-S(k)是图拉普拉斯矩阵。

（4）λ和η是正则化参数，分别平衡相应项的影响。

为了求解式（2），首先引入一个辅助变量C，则式（2）被转换为：

采用交替方向乘子法（alternating direction method of multipliers，ADMM）[30]求解式（4）。由此可获得式（4）的增广拉格朗日形式为：

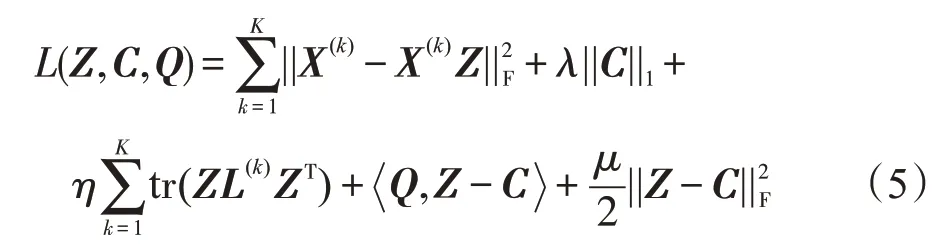
（1）固定Z和Q，优化C。

其中，cj、zj、qj和分别是C、Z、Q和的第j列，j=1,2,…,N。可以使用文献[31-32]中的策略求解式（7），式（7）有闭式解。由此可得C的更新规则如下：

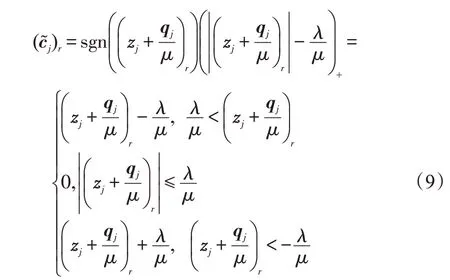
（2）固定C和Q，优化Z。

对上式Z求偏导数并使其导数为0，可得：

因此可以通过求解下式得到Z的更新公式：

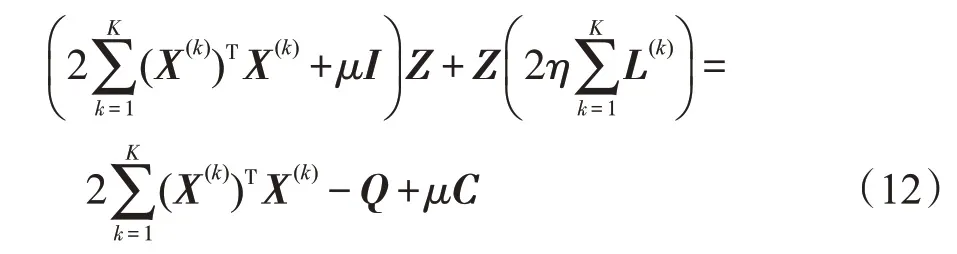
（3）固定Z和C，更新乘子Q。

乘子Q可以简单地按照以下规则更新：

因此，通过ADMM方法求解式（4）的完整的算法描述如算法1所示。

算法1ADMM方法求解式（4）

输入：给定一个多视角数据集X={X(1),X(2),…,X(K)}，共K个视角，第k个视角的样本集为1 ≤k≤K，参数λ、η。

1.初始化Q=0，Z=C=0，ρ=1.1，迭代阈值ε=10-6；

2.根据式（8）更新C；

3.通过求解式（12）更新隐视角Z；

4.根据式（13）更新Q；

5.更新μ=μρ；

6.如果||Z-C||∞＜ε，则算法停止迭代循环，否则返回步骤2；

输出：稀疏隐视角Z。

3.2 融合稀疏隐视角信息学习的多视角聚类算法

给定一个多视角数据集X={X(1),X(2),…,X(K)}，共K个视角，第k个视角的样本集为通过算法1，可以获得多视角数据共享的稀疏隐视角数据。该隐视角数据在一定程度上反映了多视角数据的全局结构信息，并且具有稀疏性。因此，基于原始的特征集和隐视角数据，本文提出了一种新的多视角聚类算法，即融合稀疏隐视角信息学习的多视角聚类算法，其目标函数为：

其中，Z=[z1,z2,…,zN]∈RN×N是隐视角数据；U是C×N的模糊划分矩阵；V={V(1)，V(2)，…，V(K)}是K个原视角的聚类中心的集合，是第k个原视角的聚类中心矩阵，表示第k个原视角的聚类i的类中心；是隐视角的聚类中心矩阵，表示隐视角的聚类i的类中心；向量w=[w1,w2,…,wK]是原视角划分权重的集合，wk是分配给第k个原视角的权重；模糊指数m＞1；α是正则化参数。

为了自适应调整各原视角的权重，式（14）引入了香农熵正则化项。让，且wk≥0，将各原视角权重看作概率分布，则其香农熵表示为。最小化负香农熵趋向于使得各个视角具有相等的重要性。β是正则化参数，用来控制香农熵正则化项的影响。

对于式（14），这里给出如下的进一步说明：一方面，如果聚类目标函数仅考虑在聚类数据上各视角的聚类紧度，即文中式（14）的第一项，则最小化该项则趋向于让类内紧度最小的视角占有很大重要性，而其他视角的作用完全被忽略；一方面，最大化各视角权重对应的香农熵，即最小化负香农熵趋向于使得各个视角具有相等的重要性，这在没有任何先验信息作指导时是合理的。上述两种情况都走上了极端，因此通过引入正则化参数β来平衡两项的作用是一种较好的处理方式，通过调节参数，可得到最佳的聚类效果。

3.3 目标函数的优化

通过迭代求解如下4个子问题最小化式（14）：

问题1固定和，并解决子问题

问题2固定并解决子问题

问题3固定并解决子问题

问题4固定并解决子问题

（1）问题1的解决方案由定理1给出。

定理1当最小化时的必要条件为：

证明利用给定的模糊划分矩阵、隐视角的类中心矩阵和权重向量，对目标函数求偏导，并令，可得：

由此定理1得证。 □

（2）问题2的解决方案由定理2给出。

定理2当最小化时的必要条件为：

证明利用给定的模糊划分矩阵、原视角的类中心矩阵和权重向量，对目标函数求偏导，并令，可得：

由此定理2得证。 □

（3）问题3的解决方案由定理3给出。

定理3当最小化时的必要条件为：

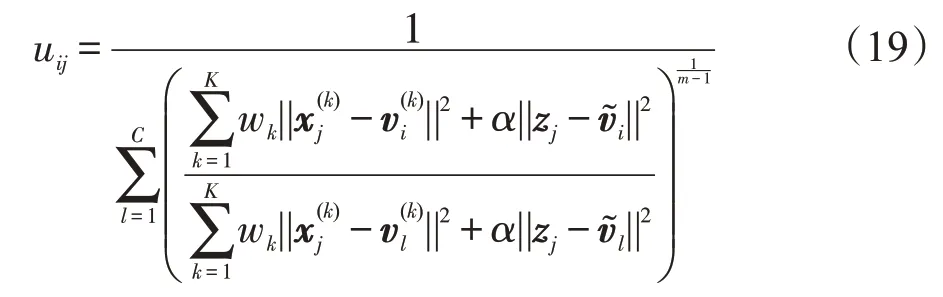
证明对于目标函数（14），由于有一个约束条件,uij∈[0,1],1 ≤j≤N，则可以建立如下的拉格朗日函数：

上式分别对uij、γ1求导，并使得导数为0，得到：

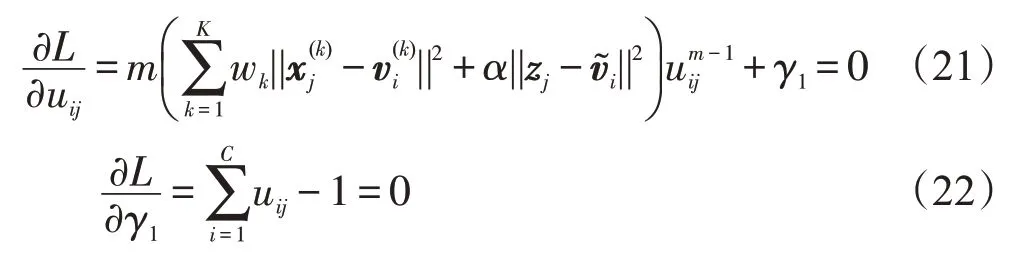
进而得到：

由此定理3得证。 □

（4）问题4的解决方案由定理4给出。

定理4当最小化时的必要条件为：

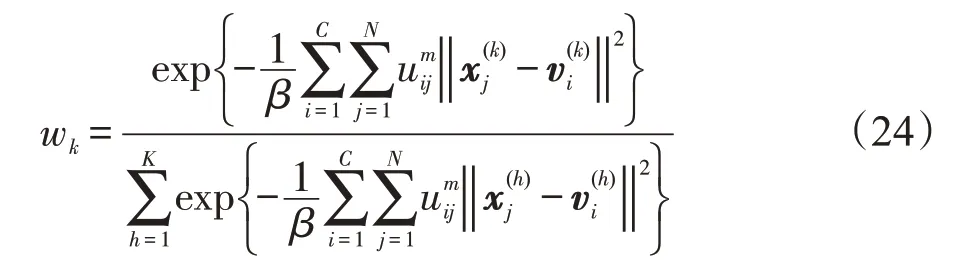
证明对于目标函数（14），由于有一个约束条件则可以建立如下的拉格朗日函数：

上式分别对wk、γ2求导，并使得导数为0，得到：

进而得到：

由此定理4得证。 □

3.4 算法描述

根据3.3节推导的参数学习规则，下面给出所提算法的具体过程，如算法2所示。

算法2融合稀疏隐视角信息学习的多视角聚类算法

输入：多视角数据集X={X(1),X(2),…,X(K)}，共K个视角，第k个视角的样本集为参数α、β，模糊指数m，迭代阈值ε，当前迭代次数t，聚类数目n。

1.由算法1得到隐视角数据Z；

2.初始化随机产生归一化的隶属度uij，随机产生归一化的原视角权重wk；

5.根据式（19）更新uij；

6.根据式（24）更新各原视角的权重wk；

7.如果||Jt+1-Jt||＜ε，则算法停止迭代循环，否则返回步骤3。

输出：模糊划分矩阵U，原视角聚类中心点隐视角聚类中心点，各原视角权重wk。

4 实验研究

4.1 数据集

为了验证本文所提算法的聚类有效性，本文选择了5个多视角数据集进行实验，这些数据集分别是Multiple Features 数据集、Image Segmentation 数 据集、Dermatology数据集、3-Sources数据集[33]和WebKB数据集。这些数据集的信息统计如表1所示。

Table1 Statistics of multi-view datasets表1 多视角数据集统计

（1）Multiple Features 数据集来自于UCI 数据集库。数据集由2 000个样本组成，其中视角1是傅里叶系数视角，该视角描述字符形状的傅里叶系数，视角2是Zernike矩视角，描述字符形状的Zernike矩。

（2）Image Segmentation 数据集来自于UCI 数据集库，由2 310个样本组成，包含两个视角，分别是形状视角和RGB视角。

（3）Dermatology数据集来自于UCI数据集库，由366个样本组成，其中视角1是组织病理学视角，视角2是临床视角。

（4）3-Sources数据集是从3个在线新闻来源收集的，选择所有3个来源报道的169个新闻故事，这些故事被手工分成6类，每个来源看作一个故事的视角。

（5）WebKB数据集由4个大学的网页组成，每个网页由3个视角组成：网页上的文本、指向它的超链接上的锚文本以及标题中的文本。选择其中1个大学的网页作为本文实验的数据集。

4.2 实验设置

为了验证本文所提算法的聚类性能，本文选择了5个聚类算法作对比。通过比较5个多视角数据集在本文所提算法和对比算法上的实验结果来验证本文所提算法的聚类性能。实验中采用的对比算法有基于多任务的组合K-means 算法（CombKM）[34]、基于样本与特征空间协同聚类的Co-clustering 算法[35]、多视角模糊聚类算法Co-FKM[18]、多视角双层变量自动加权聚类算法TW-K-means[16]、基于联合非负矩阵分解的多视角聚类算法MultiNMF[21]。

本文采用归一化互信息（normalized mutual information，NMI）36-37]、芮氏指标（rand index，RI）[37-38]、精度（Precision）[39]3种评价指标评估各聚类算法的聚类性能。3种评价指标的取值范围均为[0，1]，取值越高，表示算法的聚类性能越好。

（1）归一化互信息（NMI）

（2）芮氏指标（RI）

（3）精度（Precision）

其中，ni,j表示类i中的样本被分到第j个聚类的数据样本量；ni表示类i所包含的数据样本量；nj表示第j个聚类所包含的数据样本量；f00表示数据点具有不同的类标签并且属于不同类的配对点数目；f11则表示数据点具有相同的类标签并且属于同一类的配对点数目；N表示整个数据样本的总量大小。

在本文实验部分，采用网格搜索策略确定每个算法的最优参数，采用的寻优范围具体见表2。实验结果均由相关算法在最优参数下运行10次得到的均值及方差所组成。

4.3 实验分析

表3至表7分别显示了在5个多视角数据集上，本文所提算法和其他5个对比算法在3个评价指标上的实验结果。为了直观地比较各个算法的聚类性能，图2、图3和图4分别绘制了在所有数据集上每种算法的平均NMI、RI和Precision的值。

通过观察表3至表7的实验结果，可以得到如下的结论。

和其他聚类算法相比，本文算法在5个多视角数据集上的聚类结果都是最高的。

本文所提算法明显优于多任务的组合K-means算法CombKM。从多视角数据集在CombKM算法上的聚类结果可以看出，简单地将多视角数据样本进行融合并不能取得较好的聚类性能。

通过观察5个数据集在多视角聚类算法TW-Kmeans、Co-FKM上的结果可以看出，本文所提算法体现了一定的聚类优势。原始的多视角数据更多地反映了各视角间个性化信息。TW-K-means和Co-FKM算法在聚类过程中均只利用原始的特征集进行聚类，而忽略了共性信息对聚类效果的影响。但是，本文所提算法通过引入隐性信息使得共性信息得到有效的利用，实现了个性化信息和共性信息的协同学习，这在一定程度上提高了算法的聚类性能。

MultiNMF 算法采用非负矩阵分解策略进一步挖掘了多视角数据之间的隐性信息，提高了算法的聚类性能。但是，MultiNMF 算法仅利用隐性信息会过多地偏重于共性信息，而未能有效利用个性化信息。与MultiNMF算法不同，本文所提算法不仅挖掘多视角数据的隐性信息，而且在聚类过程实现了隐性信息和原始特征集的协同学习，大大提高了算法的聚类性能。

通过观察图2、图3和图4，可以直观地看出本文算法优于其他算法。多视角聚类算法Multi-NMF、Co-FKM和TW-K-means也都取得了良好的聚类性能。

Table 2 Parameter setting of algorithms表2 算法参数设置

Table 3 Performance of algorithms on Multiple Features dataset表3 各算法在Multiple Features数据集上的性能

Table 4 Performance of algorithms on Image Segmentation dataset表4 各算法在Image Segmentation数据集上的性能

Table 5 Performance of algorithms on Dermatology dataset表5 各算法在Dermatology数据集上的性能

Table 6 Performance of algorithms on 3-Sources dataset表6 各算法在3-Sources数据集上的性能

Table 7 Performance of algorithms on WebKB dataset表7 各算法在WebKB数据集上的性能

Fig.2 Mean NMI of each algorithm on all datasets图2 所有数据集上每种算法的平均NMI

Fig.4 Mean Precision of each algorithm on all datasets图4 所有数据集上每种算法的平均Precision

综上所述，在对多视角数据进行聚类时，本文所提算法的聚类性能优于其他聚类算法。

4.4 隐性信息的影响及分析

多视角学习的关键是如何综合利用各视角间个性化信息和共性信息，原始的各视角数据更多地反映了个性化信息，隐性信息的引入使得共性信息也得到了较充分的应用。这也是本文所提算法依据的核心思想。

为了验证将隐性信息引入到本文算法中的优势，本节对隐性信息对多视角聚类性能的影响进行了实验分析。分别在有隐性信息和无隐性信息情况下，对本文算法的聚类结果进行了比较。由于空间限制，只给出NMI指标值，具体结果见表8，另外两个评价指标与NMI有类似的结果。通过观察表8的聚类结果可以看出，隐性信息的引入有助于提高大多数数据集的聚类性能。

Table 8 Performance of algorithm with and without hidden information表8 有无隐性信息的算法性能

4.5 参数分析

正则化参数β控制香农熵正则化项的影响，为了验证该参数对本文算法性能的影响，本节针对正则化参数β进行实验。在实验中，将参数m和α固定，并逐渐改变参数β的值，其中β的取值范围为{2-6,2-5,…,25,26}。由于文章篇幅限制，只显示在Multiple Features 和Image Segmentation 两个多视角数据集上的实验结果。图5和图6分别绘制了基于NMI、RI和Precision的聚类性能，其中横坐标表示{2-6,2-5,…,25,26}从左至右的顺序序号。从图5和图6中可以看出，在2-6到26范围内，当选择一个合适的β值，可得到最好的聚类结果。

Fig.5 Performance curve with varying β on Multiple Features图5 Multiple Features上算法性能随β 变化的曲线

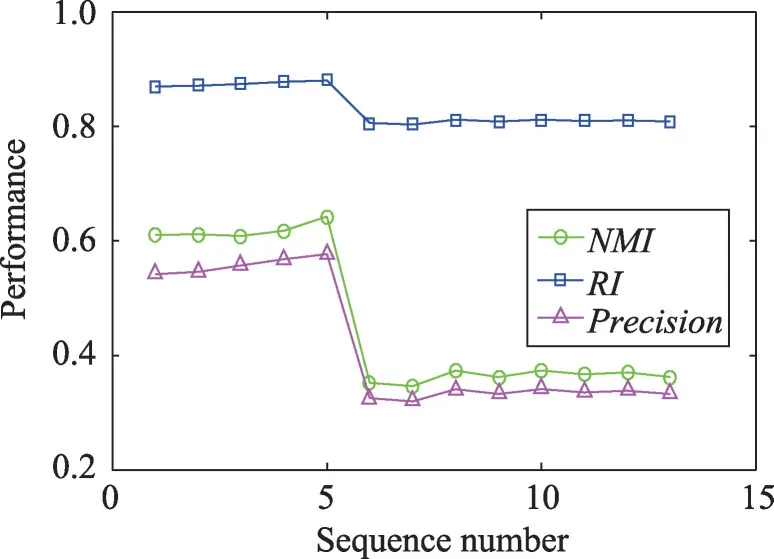
Fig.6 Performance curve with varying β on Image Segmentation图6 Image Segmentation上算法性能随β 变化的曲线

5 结束语

本文提出了一种新的多视角聚类算法，即融合稀疏隐视角信息学习的多视角聚类算法。为了从多视角数据中学习更有效的稀疏隐视角信息，本文首先提出了一种多视角稀疏隐信息学习模型，然后在聚类过程中实现原始特征集与稀疏隐视角信息的协同学习。实验研究表明，在UCI数据集和真实的多视角数据集上，所提算法在处理多视角聚类问题时相比其他聚类算法有更好的聚类性能。

虽然本文所提算法在处理多视角数据时已经取得较好的效果，但是还有很大的改进空间，比如针对高维多视角数据，引入软子空间聚类策略[36，40]来实现显隐信息的协同学习有望取得更好的聚类效果。此外，在实际应用中如何确定最优的参数，也是将来研究的重点。