结合JADE和CoDE差分算子的人工蜂群算法*

耿 璐，李艳娟

东北林业大学 信息与计算机工程学院，哈尔滨 150040

1 引言

近年来，随着计算机技术的快速发展，为了在一定程度上解决大空间、非线性、全局寻优、组合优化等复杂问题，群智能优化算法不断涌现，例如遗传算法（genetic algorithm，GA）[1]、粒子群算法（particle swarm optimization，PSO）[2]、差分进化（differential evolution，DE）[3]、免疫算法（immune algorithm，IA）[4]和人工蜂群算法（artificial bee colony，ABC）[5]。因其独特的优点和机制，这些算法得到了国内外学者的广泛关注，掀起了研究热潮。

人工蜂群算法（ABC）是Karaboga于2005年提出的一种基于蜜蜂觅食行为的群智能优化算法，并广泛应用于各个领域[6-7]。然而，ABC收敛速度较慢，主要是因为其解搜索方程虽然具有良好的全局探索（exploration）能力，但是局部利用（exploitation）能力较弱[8]。一种可能的解释是，ABC利用其解搜索方程生成候选解（新解）时每次只更改一个变量，因而后代个体继承了双亲的大部分基因，进而导致种群进化缓慢。针对这个问题，国内外学者开展了一些研究工作。例如，Gao 等人在标准ABC 的基础上，引入了一个控制参数用来决定解搜索方程中变量改变的个数[9]。Akay 等人[10]引入了一个控制参数MR（modification rate），以确定不从双亲遗传的基因的比例。刘明辉等人引入了gbest 个体提出了基于knee point 的雇佣蜂搜索机制，在加快种群进化速度提高种群多样性的同时，在收敛性以及进化方向上具有更好的效果[11]。魏锋涛等人[12]引入粒子群的全局引导机制，增强算法的“开发”能力，增强算法后期对解空间的精细搜索能力。Yu等人[13]从相关文献中研究几种有效的候选解生成策略，构建策略候选池。得到最佳候选解的解决方案被用来生成当前候选解。Brajevic[14]提出了基于交叉的ABC，用以解决约束优化问题，该算法也引入了类似的参数MR。Das 等人[15]使用Rechenberg的1/5变异规则来控制同时被干扰的变量数。上述改进在一定程度上成功地提高了ABC的性能。

不同于ABC，差分进化算法（DE）使用差分算子（变异和交叉算子）生成候选解，该候选解至少有一个变量的值与父代候选解不同。因此，DE 算法具有良好的局部利用能力，进而具有较快的收敛速度。从这个角度出发，ABC可以借鉴DE的差分算子来提高收敛速度和优化性能。

近年来，国内外学者开展了大量的结合ABC 和DE的研究工作。Abraham等人提出了HDABCA（hybrid differential artificial bee colony algorithm）算法[16]，在ABC的每次迭代后引入DE，在每次迭代后的种群中选择部分最优个体进行差分运算。Xiang 等人提出了hABCDE（hybrid evolutionary algorithm based on artificial bee colony algorithm and differential evolution）算法[17]，在每次迭代过程中顺序执行ABC和DE直到满足算法终止条件。Gao 等人提出了DGABC（DE with gbest-guided ABC）算法[18]，该算法设计了一个基于搜索经验的评价策略，每次迭代都依据该评价策略决定执行ABC 或DE。上述研究的实验结果表明引入DE能够提高ABC算法的性能。然而，上述研究工作在引入DE 时，没有考虑DE 对参数（比例因子F和交叉率CR）的敏感性问题[19-20]。因此，Liang等人提出了基于自适应差分算子的人工蜂群算法（enhanced artificial bee colony algorithm with adaptive differential operators，ABCADE）[21]。ABCADE 在 标准ABC 的雇佣蜂阶段引入了自适应差分算子，该自适应差分算子考虑了参数敏感性问题，实验结果表明ABCADE具有更好的性能。ABCADE引入的自适应差分算子主要来源于差分进化算法JADE[22]。但JADE 算法较适合解决单峰和简单多峰函数。另外一个比较经典的DE算法CoDE[23]适合求解复杂多峰函数[23]，可避免算法陷入局部最优问题。并且Li等人提出了结合JADE 和CoDE 的差分进化算法[24]，实验结果表明结合算法的性能优于JADE和CoDE。通过近期ABC、JADE 算子和CoDE 算子的相关文献，在进行彻底分析后，本文确定可以通过结合JADE算子和CoDE 算子来提高ABC 算法的性能。为此，本文提出了结合改进JADE 和CoDE 的人工蜂群算法AMDABC（adaptive modified differential operators based artificial bee colony），实验结果表明AMDABC具有更好的优化性能。AMDABC 算法的主要工作包括：

（1）分析了ABC 和DE 算法的优缺点，提出了结合DE 算子的ABC 算法，算法在雇佣蜂阶段引入JADE差分和CoDE差分算子。

（2）给出了两个控制参数P1和Q，根据P1和Q的值自适应决定采用JADE 差分算子、CoDE 差分算子还是ABC解搜索方程生成候选解。

（3）在跟随峰阶段对种群进行分级处理，重新定义了选择概率，并引入了JADE差分算子生成候选解。

2 本文提出的AMDABC算法

ABC具有良好的全局探索（exploration）能力，但局部利用（exploitation）能力较弱。与此相反，DE 具有良好的局部利用能力，但全局探索能力较弱。结合ABC和DE的混合算法能够充分利用两者的优点，成为目前的研究热点。JADE 和CoDE 是两个比较经典的DE 算法，JADE 在单峰函数和简单多峰函数性能较好，而CoDE 更适合求解多峰函数。因此，本文提出了结合JADE 和CoDE 的ABC 算法——AMDABC。AMDABC算法是ABC算法的一个改进算法，主要在雇佣蜂阶段引入JADE 和CoDE 的差分算子，并给出了相应的控制参数决定本次雇佣蜂阶段采用JADE 的差分算子、CoDE 的差分算子还是ABC的解搜索方程。

2.1 AMDABC算法框架

本文的主要目的是设计一种算法，它在雇佣蜂阶段引入一种混合框架，可以自适应地利用JADE算子、CoDE 算子和ABC 的解搜索方程，以寻求全局探索（Exploration）能力和局部利用（Exploitation）能力的平衡。

图1给出了AMDABC 算法框架，大体分为雇佣蜂阶段、跟随蜂阶段和侦查蜂阶段。在雇用蜂阶段引入了JADE 算子、CoDE 算子，并根据参数Q、Q1、Q2和P1控制候选解生成公式。在跟随蜂阶段，同样结合JADE差分算子产生候选解，以更好地解决人工蜂群算法收敛缓慢的问题，最大限度地发挥差分算子的优势。

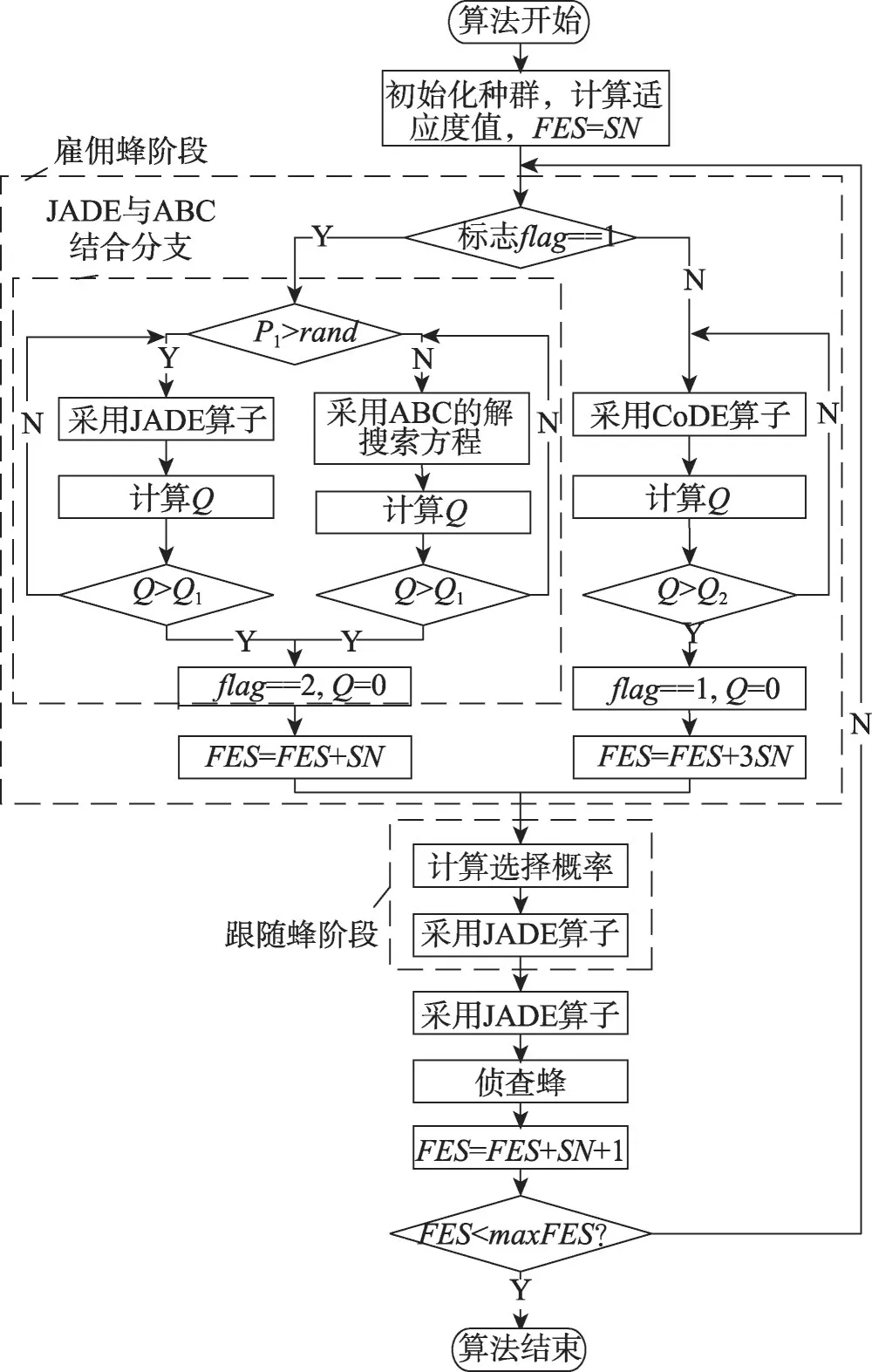
Fig.1 Algorithm framework图1 算法框架

2.2 AMDABC的雇佣蜂阶段

2.2.1 控制参数Q、Q1、Q2

AMDABC 将JADE 与ABC 的结合当作一种选择，将CoDE当作一种选择，前者适合求解单峰函数，而后者适合求解多峰函数，在雇佣蜂阶段两者根据进化情况交替执行。下面通过参数形式说明两者如何交替执行。

第G次迭代的改进率IRG定义为：

若IRG的值小于给定阈值e，则表示第G次迭代失败。参数Q用来记录迭代失败的次数，用于控制两种选择的交替执行，Q的初始值为0。

例如，假设当前执行CoDE 的差分算子，每次迭代后根据迭代是否失败来更新Q值，当Q值大于指定阈值Q2时，则执行ABC 的解搜索方程或JADE 的差分算子，Q更新为0。接下来的迭代开始执行ABC的解搜索方程或JADE的差分算子，每次迭代也不断地更新Q值，当Q值大于指定阈值Q1时，则又开始执行CoDE的差分算子。

2.2.2 控制参数P1

如图1算法框架所示，在雇佣蜂阶段，当标志flag=1时，程序进入JADE 与ABC 结合分支，此时由参数P1控制程序执行JADE算子还是ABC搜索方程。

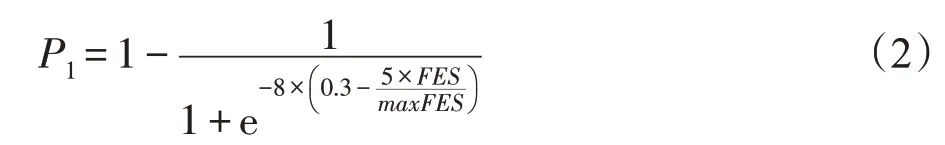
其中，FES是当前生成的个体总数，maxFES是预定义的个体总数最大值。P1随FES的增加逐渐增加，因此雇佣蜂在早期主要采用ABC解搜索方程生成候选解，保证了种群的多样性；在后期主要采用JADE 差分算子生成候选解，加快了收敛速度。

2.2.3 ABC搜索方程

在ABC算法中，对当前第i个个体Xi依据式（3）生成新个体Vi。

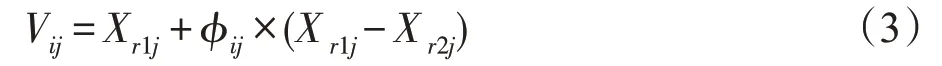
其中，i=1,2,…,SN，SN是种群大小，j=1,2,…,D，D是个体维度。r1、r2是分别从1到SN之间选择的一个整数，且不等于i。其中φij是一个-1到1之间的随机实数。

生成新个体Vi后，需要计算Vi的适应度，根据适应度决定是否用Vi更新Xi。

2.2.4 JADE差分算子

AMDABC 算法在雇佣蜂阶段和跟随蜂阶段均引入了JADE差分算子，其主要包括变异算子和两点交叉算子。

（1）变异算子：每个个体通过变异算子生成一个新解，本文采用改进后的DE/rand/1变异算子[18]，具体如式（4）所示。

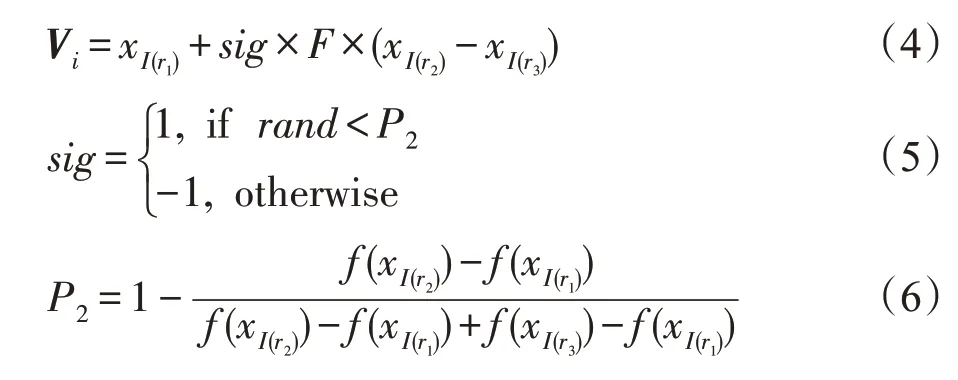
其中，xI(r1)、xI(r2)、xI(r3)分别表示随机选择3个个体中的最好的、次好的和最坏的个体。sig的定义如式（5）所示，其用来控制差分向量的方向。在式（6）中，xI(r1)是相对最有希望的区域。如果3个随机选择的个体具有相等的函数值(f(xI(r1))=f(xI(r2))=f(xI(r3)))时，P2的值设置为0.5。

（2）两点交叉算子：变异操作执行完毕后，AMDABC 对当前个体Xi和变异个体Vi执行两点交叉运算，生成候选向量Ui=(ui1,ui2,…,uiD)，具体公式如式（7）所示。

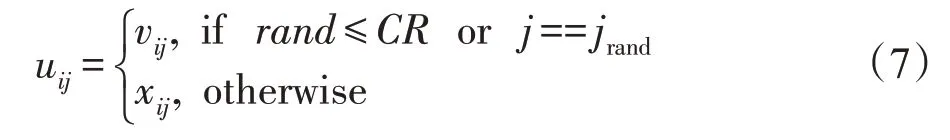
其中，i=1,2,…,SN，SN是种群大小，j=1,2,…,D，D是个体维度，rand是一个0到1之间的随机数，jrand是1到D之间的一个随机整数，其保证了至少有一个变量遗传自变异向量Vi。CR是交叉参数，其取值范围为[0，1]。

（3）参数F和CR的自适应调整：在JADE 中，式（4）和式（7）的比例因子F和交叉率CR的设置可能影响算法的性能。为解决这个问题，本文采用了一种自适应机制对参数F和参数CR进行了调整，假定其服从高斯分布[24]。

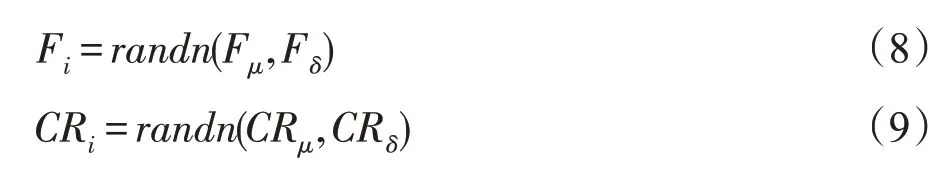
其中，Fi和CRi均为0到1之间的实数，当Fi＞1或者Fi≤0时，Fi被[0，1]范围内生成的随机数代替，同样的约束也适用于CRi。Fμ、CRμ初始值为0.5[22]，Fδ、CRδ初始值为0.3[19]。

每次迭代，当产生了新的候选解，其相关的Fi和CRi分别保存在SF和SCR中，在每一代的末尾，分别根据式（10）和式（11）更新参数Fμ和Fδ。CRμ和CRδ采纳相同的更新方法。

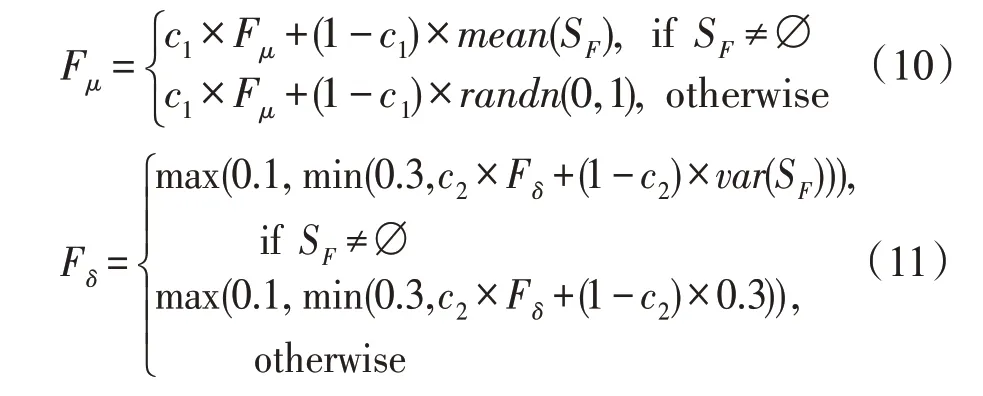
mean(SF)和var(SF)分别代表的是当前SF的平均值和方差。Fδ和CRδ的范围限制在[0.1，0.3]。

2.2.5 CoDE差分算子

AMDABC算法在雇佣蜂阶段引入了CoDE差分算子。对每个个体，CoDE分别通过差分进化算子“DE/rand/1/bin”“DE/rand/2/bin”和“DE/current-to-rand/1”生成3个候选解，然后选择一个适应度值最大的候选解作为当前候选解。根据当前候选解和当前个体适应度值的大小来决定是否用当前候选解替代当前个体。

其中，r1、r2、r3、r4、r5是1到SN之间的一个随机整数，且与i不同且互不相同，代表一个个体。xbestj是当前群体中的最好个体。

此外，随机使用的3组F和CR控制参数设置分别为[F=1.0,CR=0.1]，[F=1.0,CR=0.9]，并且[F=0.8,CR=0.2]。

2.3 AMDABC的跟随蜂阶段

在跟随蜂阶段，每个跟随蜂估量种群个体的质量，并依据质量按照一定的概率选择个体。基本ABC 算法为每个个体计算选择概率，然后依据概率决定选择哪个个体。理论上概率较大的个体被选择概率较大。但当个体数目较多时，每个个体的选择概率都比较小，不同个体之间的选择概率差异也比较小，这样不容易区分个体之间的差异性。为了克服上述问题，本文采用将个体分成n个级别，每个级别的个体具有相同的选择概率，这样只需要计算n个不同的选择概率，能够较好地区分不同级别的个体，保证跟随蜂能以较高概率在较好级别中选择个体。假定将所有候选解等分为n个级别，每个级别包含m=SN/n个个体。最好的m个候选解级别为n，最后m个候选解级别为1。每个候选解被选择的概率依据式（15）进行计算。

其中，Pi和Li分别是选择概率和第i个个体的级别。为了避免超级个体提前诱导整个蜂群丢失种群多样性，防止过早陷入局部最优，m不可取值较小；同时个体之间需强调差异性，算法需要快速收敛，m不可取值较大。通过设计重复性实验确定SN=50时，m为5时效果最优。依据式（15）可以看出，级别越高，选择概率越大，同一级别的个体的选择概率是相同的。通过这种方式，跟随蜂能够有效地识别出良好的候选解，并在有前途的区域进行局部精细搜索。同一级别的个体具有相同的选择概率，这表明跟随蜂平等对待相似位置，因此可以同时利用局部最优区域。跟随蜂选择一个个体后采用JADE 变异算子和两点交叉算子产生候选解。

3 实验

3.1 测试数据和参数设置

为测试本文算法AMDABC性能，使用了19个标准函数进行测试，具体公式如表1所示。其中，D是测试函数的维度。函数f1～f6和f8是连续的单峰函数，f7是一个不连续的阶跃函数，f9是一个噪声四次函数，f10～f19是局部最小值随着问题维度呈倍增长的多峰函数，Range是变量的取值范围，Min是函数理论最小值，Accept是可接受的最小值。

Table 1 Standard test function表1 标准测试函数

本文算法和比较算法参数设置如表2所示，所有比较算法的参数设置情况和原文一样。

3.2 与典型ABC改进算法的比较

AMDABC与典型的ABC改进算法进行比较，具体包括MABC（modified artificial bee colony algo-rithm）[10]、GABC（global-best-guided artificial bee colony algorithm）[8]、CABC（crossover artificial bee colony algorithm）[25]。MABC试图通过在解搜索方程中同时改变多个变量来提高人工蜂群的性能。GABC 将全局最优解的信息结合到解搜索方程中以提高解搜索方程效率。CABC 通过改进解搜索方程来提高算法搜索能力及加快收敛速度。在19个标准函数上，分别进行了两个数据维度（D=30和D=50）的实验比较。所有算法独立运行25次，参数masFES的值设置为5 000D，计算25次独立运行的均值和方差。具体实验结果见表3和表4，其中mean表示均值，std表示方差，win表示算法在19个测试函数上取得最优结果的个数，其中对取得最优结果的情况进行了加粗处理。

Table 2 Parameter settings of AMDABC and comparison algorithms表2 AMDABC及比较算法的参数设置

如表3所述，在测试函数的维数等于30时，AMDABC 算法能够在7个函数上找到全局最优解（即f7、f11～f14、f17、f18），在其余的函数中取得的解也非常接近于函数本身的全局最优解。依据函数取得最优解个数来评价，AMDABC 在除了函数f19之外的所有函数上取得了最优结果，取得最优解个数为18，其他算法分别为1、3、7，因此依据取得最优解个数来说，AMDABC算法优于其他算法。整体来说，AMDABC的性能在大部分测试函数上明显优于MABC、GABC和CABC。

如表4所述，在测试函数的维数等于50时，AMDABC 算法能够在5个函数上找到全局最优解（即：f7、f11～f13、f18），在其余的函数中取得的解也非常接近于函数本身的全局最优解。依据函数取得最优解个数来评价，AMDABC在除了函数f16、f17和f19之外的所有函数上取得了最优结果，取得最优解个数为16，其他算法分别为1、4、7，因此依据取得最优解个数来说，AMDABC 算法优于其他算法。整体来说，AMDABC 的性能在大部分测试函数上明显优于MABC、GABC和CABC。

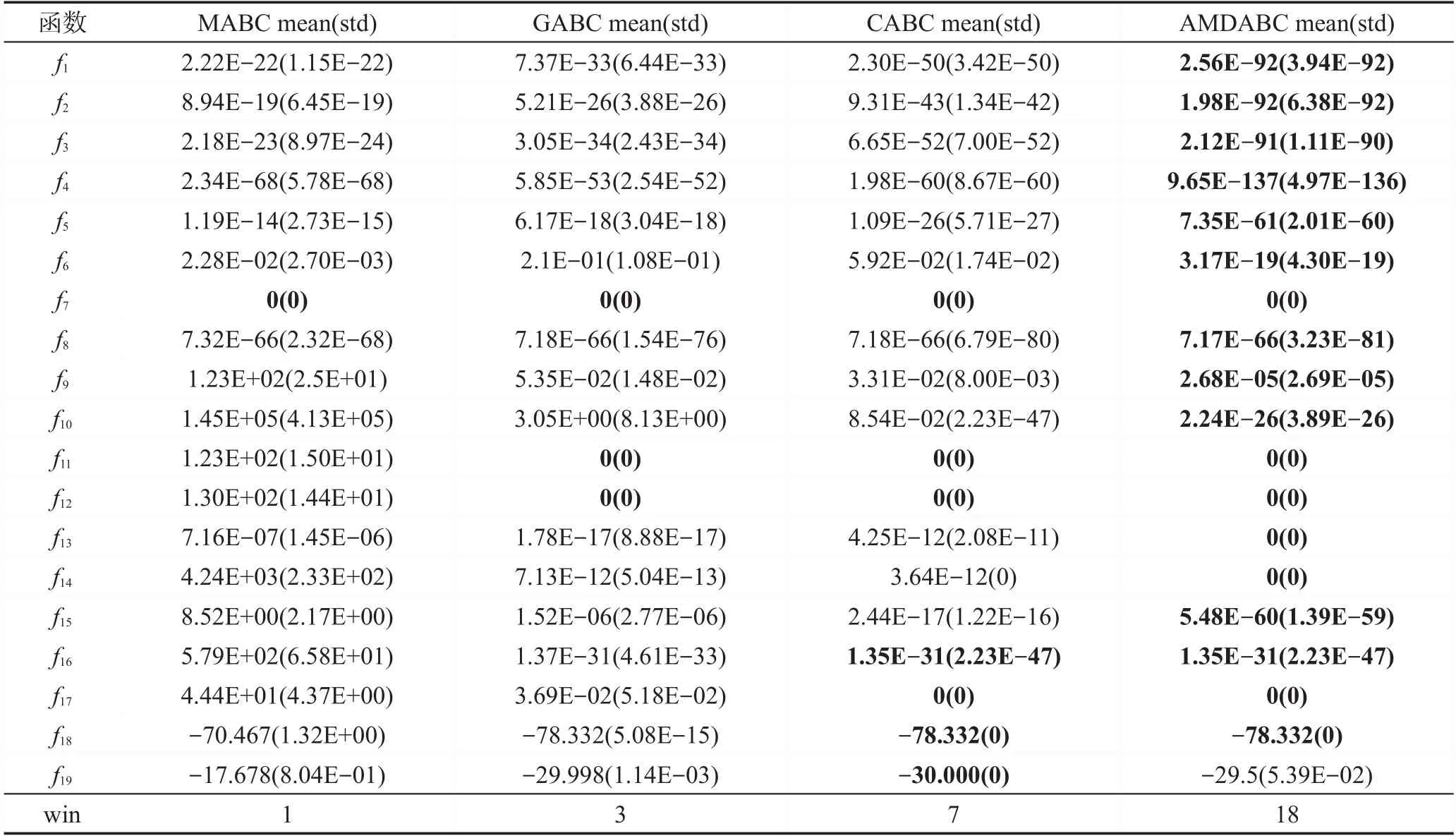
Table 3 Experimental results compared with improved ABC algorithms（D=30）表3 与典型ABC改进算法比较实验结果（D=30）

Table 4 Experimental results compared with improved ABC algorithms（D=50）表4 与典型ABC改进算法比较实验结果（D=50）

图2给出了一些代表性函数在数据维数D=30时独立运行25次的均值曲线图，其中横坐标FES 表示当前生成的个体总数，纵坐标表示均值。曲线越陡，收敛速度越快。表3、表4和图2说明了本文算法AMDABC具有更好性能。

目前在文献中，数值实验被广泛用于验证算法的收敛性能。如表5所述，本文根据常用的指标AVEN将AMDABC 和典型ABC 算法（MABC、GABC 和CABC）进行比较，以证明算法有较好的收敛性能。AVEN 表示达到可接受值时所需的FES 的平均数量。显然，AVEN越小，收敛性能越好。

3.3 与经典DE改进算法的比较

本文算法AMDABC遵循人工蜂群算法的框架，但因其与差分进化也密切相关，因此将它与差分进化算法比较是必要的。并且由于结合ABC 和DE 的混合算法能够充分利用上述两种算法的优点，国内外学者已开展了大量的ABC 和DE 的混合算法的研究工作。本节将AMDABC与5种典型的差分进化算法进行比较，具体包括SaDE（self-adaptive differential evolution）[19]、sinDE（sinusoidal differential evolution）[20]、JADE[22]、CoDE[25]和ABCADE[21]。其中ABCADE算法是典型的ABC 和DE 结合算法。在19个标准函数上，分别进行了两个数据维数（D=10，D=40）的实验比较。所有算法独立运行25次，参数masFES的值设置为5 000D，计算25次独立运行的均值和方差。具体实验结果见表6和表7，其中mean表示均值，std表示方差，win表示算法在19个测试函数上取得最优结果的个数，其中对取得最优结果的情况进行了加粗处理。

Fig.2 Mean convergence curve compared with typical ABC improved algorithms(D=30)图2 与典型ABC改进算法比较的均值收敛曲线（D=30）

Table 5 AVEN comparison with typical ABC improved algorithms（D=40）表5 与典型ABC算法的AVEN比较（D=40）

Table 6 Experimental results compared with typical DE improved algorithms（D=10）表6 与典型DE改进算法比较实验结果（D=10）

如表6所述，在测试函数的维数等于10时，AMDABC 算法能够在6个函数上找到全局最优解（即：f7，f11～f14，f18），并且方差为0，也就是说每次独立运行都可以获得全局最优解；在其余的函数中取得的解也非常接近于函数本身的全局最优解。依据函数取得最优解个数来评价，AMDABC在除了函数f16、f17、f19之外的所有函数上取得了最优结果，取得最优解个数为16，其他算法分别为1、2、2、5、9，因此依据取得最优解个数来说，AMDABC 算法优于其他算法。整体来说，AMDABC 的性能在大部分测试函数上明显优于SaDE、CoDE、JADE、sinDE和ABCADE。

如表7所述，在测试函数的维数等于40时，AMDABC 的性能进一步得到了改善，AMDABC 算法能够在7个函数上找到全局最优解（即：f7、f11～f14、f17、f18），并且方差为0，也就是说每次独立运行都可以获得全局最优解；在其余的函数中取得的解也非常接近于函数本身的全局最优解。依据函数取得最优解个数来评价，AMDABC 在除了函数f4和f19之外的所有函数上取得了最优结果，取得最优解个数为17，其他算法分别为1、2、3、2、9，因此依据取得最优解个数来说，AMDABC 算法优于其他算法。整体来说，AMDABC 的性能在大部分测试函数上明显优于SaDE、CoDE、JADE、sinDE和ABCADE。

图3给出了一些代表性函数在数据维数D=40时独立运行25次的均值曲线图，其中横坐标FES 表示当前生成的个体总数，纵坐标表示均值。曲线越陡，收敛速度越快。表6、表7和图3说明了本文算法AMDABC具有更好性能。

上述比较实验结果表明AMDABC 算法性能优于典型ABC 算法、典型DE 算法、典型ABC 和DE 结合算法。

3.4 Q1与Q2的参数敏感性分析

AMDABC 算法的雇佣蜂阶段主要包括两个分支，一个分支是ABC 与JADE 结合（简称为分支1），一个分支是CoDE 算法（简称为分支2），在两个分支之间交替执行。算法首先不断地执行分支1，直到分支1失败的次数大于参数Q1时则开始不断地执行分支2。当分支2失败的次数大于参数Q2时则又开始执行分支1。综上，AMDABC算法依据参数Q1和Q2的值自适应地交替执行两个分支，参数Q1和Q2的值可能影响AMDABC算法的性能，本节通过实验分析参数Q1和Q2的敏感性。

Table 7 Experimental results compared with typical DE improved algorithms（D=40）表7 与典型DE改进算法比较实验结果（D=40）

AMDABC 算法的分支1包含一个变异算子，而分支2包含3个变异算子，因此Q1的值需要大于等于Q2的值。在保证其余参数值不变的情况下，本文测试了Q1和Q2的7种取值组合，并将其与本文设置的参数组合（Q1=10，Q2=5）进行比较。在测试函数的维数等于30时，每个组合单独运行19次，通过Wilcoxon秩和检验考虑在5%的显著性水平上检验显著性差异，最终对比结果如表8所示。

从表8可以看出，后4组组合（Q1=2Q2）的性能略优于前3组组合（Q1=Q2）的性能，主要是因为Q1控制的分支1每次只执行1次变异操作，而Q2控制的分支2每次执行3次变异操作，两个分支变异操作的优势互补，在Q1大于Q2时能更好地自适应调整两个分支，保证两个分支更公平地竞争，因此后4组组合（Q1=2Q2）的性能略优于前3组组合（Q1=Q2）的性能。

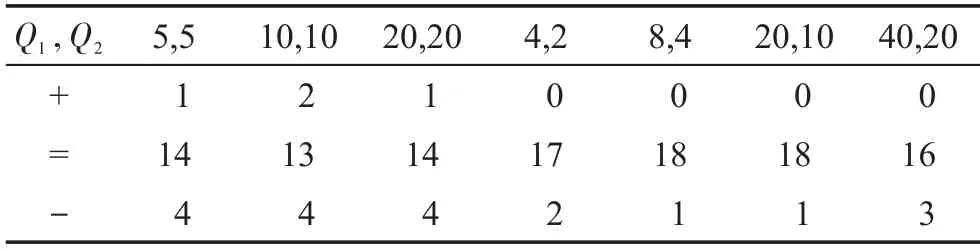
Table 8 Sensitivity analysis of Q1and Q2表8 Q1与Q2的参数敏感性分析

如表8所示，在Q1=2Q2的4组组合中，组合（40，20）的性能最差，说明Q1、Q2的值较大时，AMDABC算法性能会降低。一个合理的解释是随着Q1、Q2值的增大，在同一蜜源处搜索新解的次数会增加，会产生一些没有必要的搜索，导致算法性能降低。组合（4，2）的性能较差，说明Q1、Q2的值较小时，AMDABC 算法性能也会降低。一个合理的解释是Q1和Q2较小时，在同一蜜源处搜索新解的次数较少，不能保证算法搜索到较优的新解。不过从整体上来看，后4组组合的性能与本文设置的组合（10，5）的性能都比较接近，因此在保证Q1大于Q2的情况下，本文算法对这两个参数在大部分测试函数上是不敏感的。综上所述，建议Q1、Q2组合设置范围为（8，4）～（20，10）。

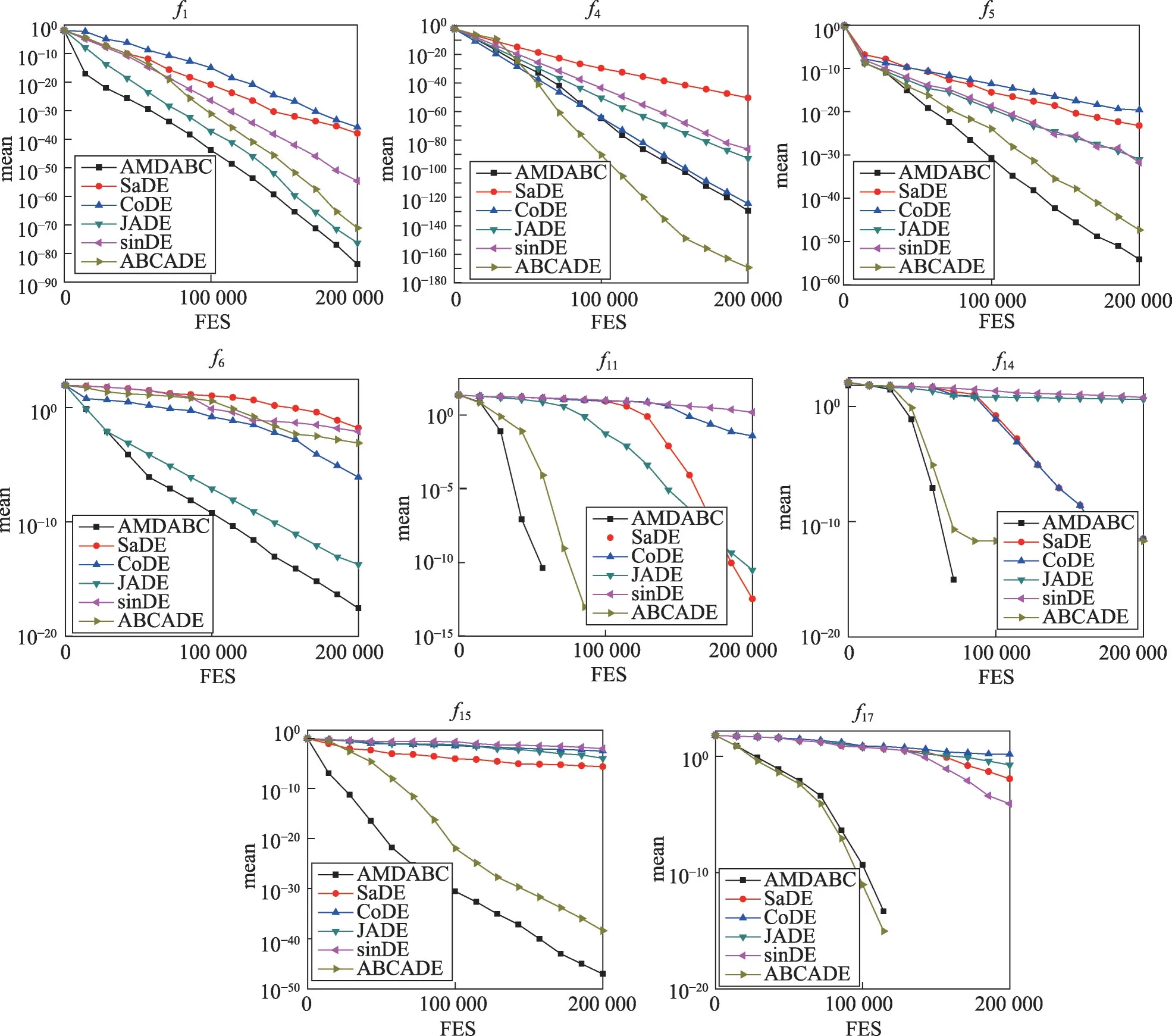
Fig.3 Mean convergence curve compared with typical DE improved algorithms(D=40)图3 与典型DE改进算法比较的均值收敛曲线（D=40）

4 结束语

本文提出了一个改进的人工蜂群算法AMDABC，它在人工蜂群算法的框架下结合了差分进化算子，主要包括JADE 和CoDE 的差分算子。在雇佣蜂阶段，通过两个控制参数P1和Q决定雇佣蜂采用JADE差分算子、CoDE差分算子还是ABC解搜索方程生成候选解。在跟随蜂阶段，使用JADE变异算子和两点交叉算子产生候选解。在19个标准函数的不同数据维数上，AMDABC 的性能与典型的人工蜂群算法、典型的差分进化算法、人工蜂群与差分进化结合算法的性能进行了比较，实验结果表明AMDABC 算法性能优于典型ABC 算法、典型DE 算法、典型ABC 和DE 结合算法。在未来的工作中，可以考虑将更有效的差分进化算子和人工蜂群算法的解搜索方程结合，也可考虑将AMDABC算法用于处理更复杂的优化问题和现实世界的应用。