高斯核密度估计方法检测健康数据异常值

王 康，周治平

江南大学 物联网工程学院，江苏 无锡 214122

1 引言

随着人们越来越关注更加健康的生活方式，运动手环佩戴者的数量也在不断增加。运动手环可以监控和跟踪用户日常活动，如运动、睡眠以及卡路里等[1]。用户通过呈现的数据信息，了解自身的活动情况。Lim等[2]发现一些特定疾病患者的手环数据与健康佩戴者数据存在差异，且特定的指标与某种疾病的关联较大。对于正常佩戴者而言，并不知晓其身体的疾病隐患，在缺乏对这些数据进行有效分析的情况下，仅从简单的手环数据呈现中也无法判断得知。对于手环采集的活动数据，异常是指数据以及关联某些特定疾病的指标偏离个体基准的情况。因此，对运动手环采集的健康数据进行有效挖掘，判断数据异常关联，分析导致数据异常的因素，对改善用户生活方式，提升用户健康状况具有重要作用。

异常检测也被称作离群检测，目的是发现在不同机制下，那些区别于大部分数据，且足够引起怀疑的少部分数据。学者们使用多种机器学习方法致力于提高离群检测的效率。Knorr 等[3-4]提出基于距离的离群点检测方法，摆脱了离群点检测算法中对数据的分布模型和分布参数的限制。随后，Boriah 等[5]基于K-近邻算法衡量对象的离群度，该方法可以处理大规模数据集。朱利等[6]提出一种快速K-近邻的最小生成树离群检测方法，该方法基于距离比值的加权排序离群因子，能大幅降低时间复杂度，提高计算效率。Breunig 等[7]提出基于密度的离群点检测算法，给出对象是离群点的程度定量度量，通过考察对象与其近邻“密度”的差异来判断该对象是否为离群点，这种差异通过局部离群因子（local outlier factor，LOF）衡量。但由于LOF算法基于欧氏距离，当数据点之间存在特殊分布时，对象之间的相似程度无法由欧式距离准确反映出；并且此方法不适用于高维数据，高维空间数据的高度稀疏性使得数据点之间几乎是等距离的，每个数据点在密度的意义上都可以看作是一个异常点。Ghoting 等[8]针对处理高维数据集的问题，提出二段算法RBRP（recursive binning and reprojection）。该算法基于索引提高计算效率，循环嵌套减少操作I/O次数，降低时间复杂度。Tang等[9]引入链式距离的概念，通过计算对象与其K-近邻的边长度加权和，提出基于连通性的离群因子（connectivity-based outlier factor，COF）。He 等[10]基于聚类提出聚类离群因子（cluster based local outliers factor，CBLOF）算法，一方面能够检测出离群簇，另一方面又提高了局部离群点的检测精度。Zhu 等[11]结合最小生成树提出KNMOD（K-nearest neighbor and minimum spanning tree-based outliers detection）算法，降低时间复杂度，提高检测效率。钱景辉等[12]采用多示例学习（multi-instance learning，MIL）框架，结合退化策略和权重调整方法检测局部离群点。Xu等[13]基于核密度估计（kernel density estimation，KDE）提出一种新的离群检测算法，该算法在利用KDE 计算数据概率密度函数最优估计的基础上，建立信度函数检测离群点。杨宜东等[14]利用核密度估计方法，实现全局数据的离群点检测。Ngan等[15]验证了核密度估计方法在大规模的数据集上比One-Class SVM 具有更好的离群检测效果。Tang 等[16]考虑反向最近邻并且共享对象的最近邻以进行核密度分布估计，提出基于相对密度的离群值得分（relative density-based outlier score，RDOS）来测量对象的局部离群程度。胡彩平等[17]引用信息熵的概念，同时利用加权距离来代表各对象之间的距离，提出基于密度的局部离群点（density-based local outlier factor，DLOF）算法。Xia 等[18]通过网格划分和扩展，提出CRF（complete random forest）算法，并引入投票机制，更有效地分离离群点，但网格的数量随着维数呈指数级增长，时间复杂度会迅速增加，降低了算法的性能。

鉴于此，针对运动手环数据存在与健康状况关联异常值且手环数据在高维空间的高度稀疏性降低异常检测准确率的问题，本文提出了一种基于高斯核密度估计的离群点检测方法。该方法在采用t-SNE（t-distributed stochastic neighbor embedding）算法[19]对数据集进行特征提取的基础上，利用高斯核函数改进LOF算法，计算局部离群因子，据此检测出离群点。

2 高斯核密度估计方法原理

2.1 高斯核密度估计局部离群因子算法

高斯核密度估计局部离群因子算法的详细描述如下：

（1）高斯核局部密度估计

设k为正整数，则对象m的高斯核局部密度为：

式中，G(∙)表示高斯核函数；||xn-xm||表示对象m和对象n的欧式距离；σ为所有样本点两两之间距离的标准差，整个样本点之间距离的变化程度可以引用标准差来反映。

式（2）表示对象m和n的高斯核距离。高斯核局部密度基于高斯核距离，对象m的K-近邻邻域可以通过计算各点与m的高斯核距离来确定。同时，对象m和其近邻点之间距离的衰减程度也可由高斯核距离反映。对于离群点，它们与邻近点之间距离的衰减程度大于正常点，因此它们的高斯核局部密度较小。相反，正常点与邻近点之间距离的衰减程度较小，因此它们的高斯核局部密度接近于1。

（2）高斯核局部离群因子

对象m的高斯核局部离群因子记作：

在被检测样本点中，那些高斯核局部密度低于近邻点的样本点被视作离群点。若m是被检测的点，n是m的一个邻近点。由式（1）、式（2）可知，如果m是离群点而n是正常点，那么有Dk(n)＞Dk(m)。由式（3）可知Fk(m)＞1。如果m和n都是正常点，那么Dk(n)≈Dk(m)，Fk(m)≈1。通过比较Fk(m)和1的大小可以区分正常点和离群点。

2.2 稳定性分析

对高斯核密度估计局部离群因子算法判定阈值的稳定性进行如下分析。首先，对于任意对象m，给出如下定义：

其中，dmin(m)、dmax(m)分别是m的K-近邻邻域中距离m最近的点与最远的点的距离：imin(m)、imax(m)分别表示m的K-近邻对象的K-近邻邻域内距离样本中心的最小距离和最大距离。假设对象m为任意数据集D中的一个样本点，正整数k满足1 ≤k≤|D|，对象m的Fk(m)满足：

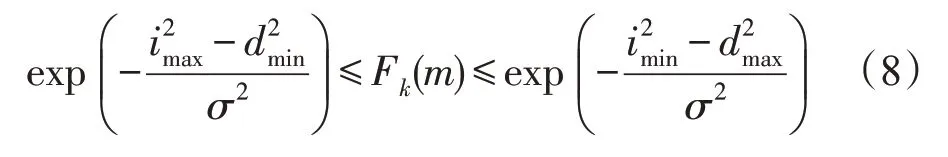
证明如下：

由式（9）可知，对象m的Dk(m)满足：

对象o为对象n的K-近邻邻域中的一点，对于任意o满足：

由式（11）可知，对象n的Dk(m)满足：

由式（10）、式（12）可知，对象m的Fk(m)满足：

由式（8）可知，对象m的Fk(m)值的上下限较为紧密，如果m为正常对象，则有d≈i，其Fk(m)的上下边界值均趋近于1，因此对象m的Fk(m)值也趋近于1。可以用1作为阈值，判定正常点与离群点。

3 高斯核密度估计方法实现流程

3.1 算法实现

（1）样本数据集预处理

本方法首先对采集到的手环样本数据进行预处理。通过运动手环能够采集到用户一天内步数、心率（设定为一分钟采集一次）、卡路里、全天睡眠时间、深度睡眠时间、浅睡眠时间等一系列数据。数据集包含M个用户T天的活动数据，经过选取i个特征指标后，每一条运动数据可以表示为i维向量X=[x1,x2,…,xi]T。根据用户活动类型可将其分为轻运动、静坐、运动以及睡眠四类，这样可以较完整地反映用户一天的活动情况。因此，本文选取的特征指标为总心率均值、总心率峰值、轻运动心率均值、轻运动心率峰值、静坐心率均值、静坐心率峰值、运动心率均值、运动心率峰值、睡眠心率均值、睡眠心率峰值、步数、卡路里、全天睡眠时间、深睡眠时间、浅睡眠时间。

（2）特征提取

在高维空间中，随着数据规模的增加，时间复杂度会迅速增加，性能急剧下降；同时，数据在高维空间中具有高度稀疏性，这使得每个数据点之间几乎等距，从而在密度的意义上都可被视作异常点，导致检测算法的准确率大大降低。由文献[19]可知t-SNE算法将高维数据映射在二维空间中，使得高维度下距离较近即相似的数据映射后更聚合，较远的更疏远，较好地捕捉了数据的整体特性，提高了局部结构能力。因此本文采用t-SNE 算法对高维数据进行特征提取，为后续在二维空间计算所有样本的Fk(m)值提供支撑。

（3）计算每条数据的GKDELOF（Gaussian kernel density estimation-based local outlier factor）值

将特征提取后的二维数据集作为输入，由以下公式计算每个对象m的Fk(m)值。

用Fk(m)值对对象的离群程度进行量化，并与离群程度阈值1比较，输出样本数据离群点。

3.2 算法伪代码

输入：所有数据点组成的集合，记为S；特征提取后数据点组成的集合，记为T；数据集的维度数，记为D；特征提取维度数，记为d；所有数据点的K-近邻集。

输出：数据集的离群点集合O。

4 仿真实验

仿真实验基于Matlab 2015b、PyCharm 平台，计算机的硬件配置为：Windows 10操作系统、Intel Core i5-5200U CPU、3.2 GHz、16 GB RAM。

本文选取了8个数据集，皆来自UCI机器学习数据库，这些数据集包含异常类，根据数据集的特点，将其中一部分数据作为异常数据。数据集的数据特征见表1。

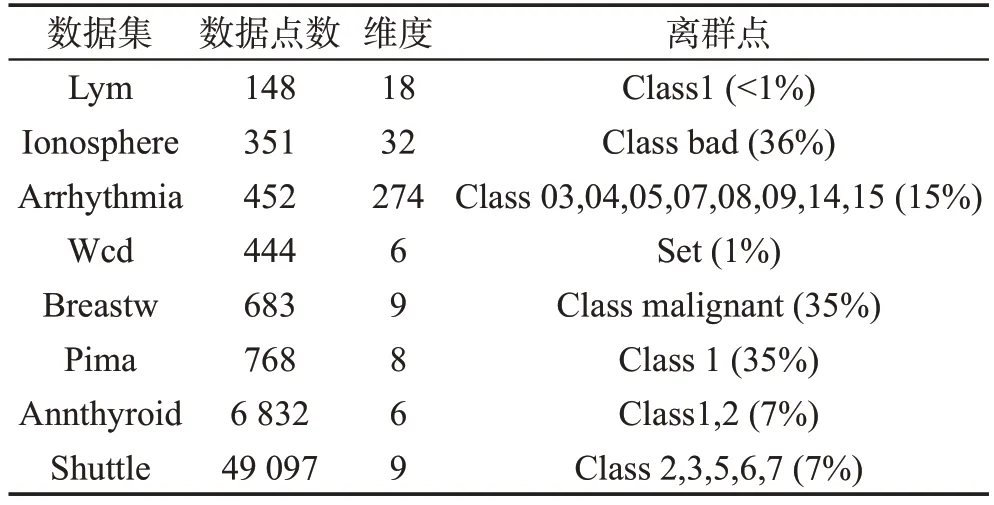
Table 1 Data set information表1 数据集信息表

为检验算法的准确性，将本文算法与基于密度的LOF[7]算法、基于聚类的CBLOF[10]算法、基于核密度的文献[16]算法、基于网格划分的IForest[20]算法进行了比较。选取理由为，本文是对于LOF 算法的改进，因此选取LOF 算法作为对比算法；CBLOF 算法是基于聚类的经典离群检测算法；文献[16]的算法是基于密度并利用核密度分布估计从而检测离群点，本文也是将核密度作为一个改进点；IForest算法是目前较新的基于网格划分的算法，检测效果较好，广泛使用。

本文所用的评估异常检测算法的主要性能指标包括正确率（accuracy，ACC）、假负率（false negative rate，FNR）、假正率（false positive rate，FPR）和AUC（area under curve）。一个较优性能的异常检测算法应该具有较低的FNR和FPR，以及较高的ACC和AUC。

4.1 实验结果对比与分析

为验证本文方法的适用性，由本文方法检测不同数据集后绘制的ROC曲线图如图1所示。

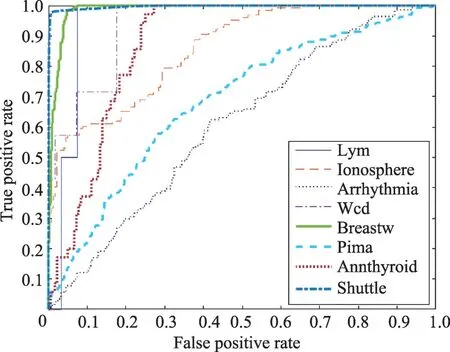
Fig.1 ROC curve of different data sets by GKDELOF图1 GKDELOF算法检测不同数据集的ROC曲线

从图1的ROC 曲线结果图可以看出，本文提出的高斯核密度估计异常值检测方法在不同数据集上都取得了较好的效果。其中，在Shuttle 数据集上取得了最好的检测效果；仅在Arrhythmia 和Pima 数据集上的效果较不理想。对ROC曲线的定量分析结果如表2中的AUC值所示。

为验证本文方法中特征提取对于处理高维数据的检测准确率的提高，取文献[18]中使用的维度较高的两个数据集，分别为Isolet1234（618维）和Madelon（500维）以及表1中的Arrhythmia（274维）数据集。分别在经过特征提取和未经过特征提取的情况下（下标有l的为经过特征提取处理的），利用本文所提出的算法进行ROC曲线的对比，对比结果如图2所示。

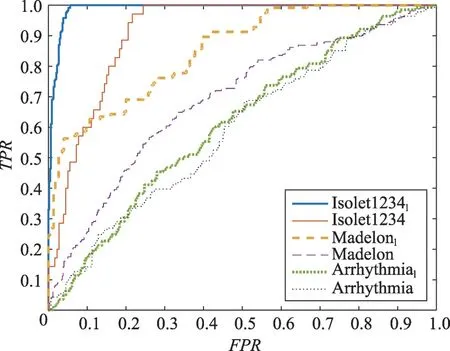
Fig.2 Comparison of ROC curves before and after dimensionality reduction of high dimensional data图2 高维数据降维前后ROC曲线比较

由图2对比结果可以知道，3个数据集在经过特征提取后，检测的效果都有一定的提升。根据ROC曲线下面积AUC值得出，在经过降维处理之后，提升最明显的是Madelon数据集，AUC值为0.85。Isolet1234数据集次之，AUC值提高了13%。在Arrhythmia 数据集上的提升效果并不明显，主要是由于数据集中定类属性较多，对于定类属性值的运算不能真实度量样本相似性，因此影响了检测精度。此实验说明运用t-SNE 算法提取特征后，对于高维数据，能够进一步提升检测效果。

由于本文算法和LOF 算法以及文献[16]的算法都需要采用最近邻方法，因此为了评估不同k值对算法性能的影响，本文对于这3个算法，作用在Shuttle数据集上，取多次不同k值，对比各个算法的AUC值，结果如图3所示。

从图3中可以看出本文算法在取不同k值时的表现都优于其他两种算法，并且当k=5时，对于本文算法性能的提升是最大的，此后的AUC值一直稳定在0.96以上。

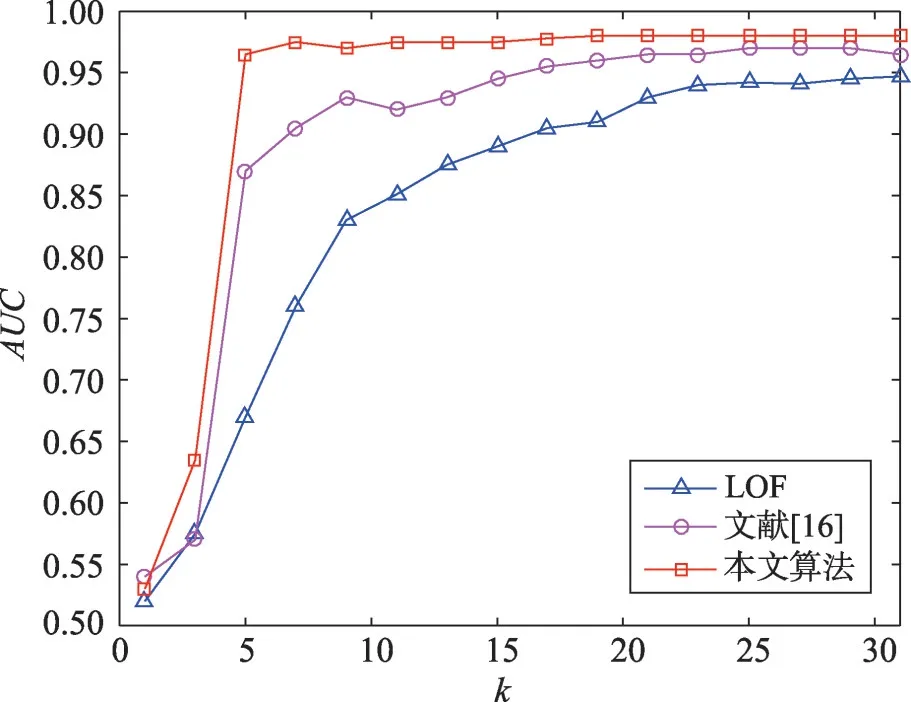
Fig.3 Performance of AUC with different k values for data set of Shuttle图3 在Shuttle数据集上不同k值时的AUC值

为验证本文算法的优势，将本文算法与LOF 算法、CBLOF 算法、文献[16]算法和IForest 算法作对比，计算评估离群检测算法的性能指标，即ACC、FNR、FPR和AUC，结果放入表2。各算法的参数设置如表3所示。

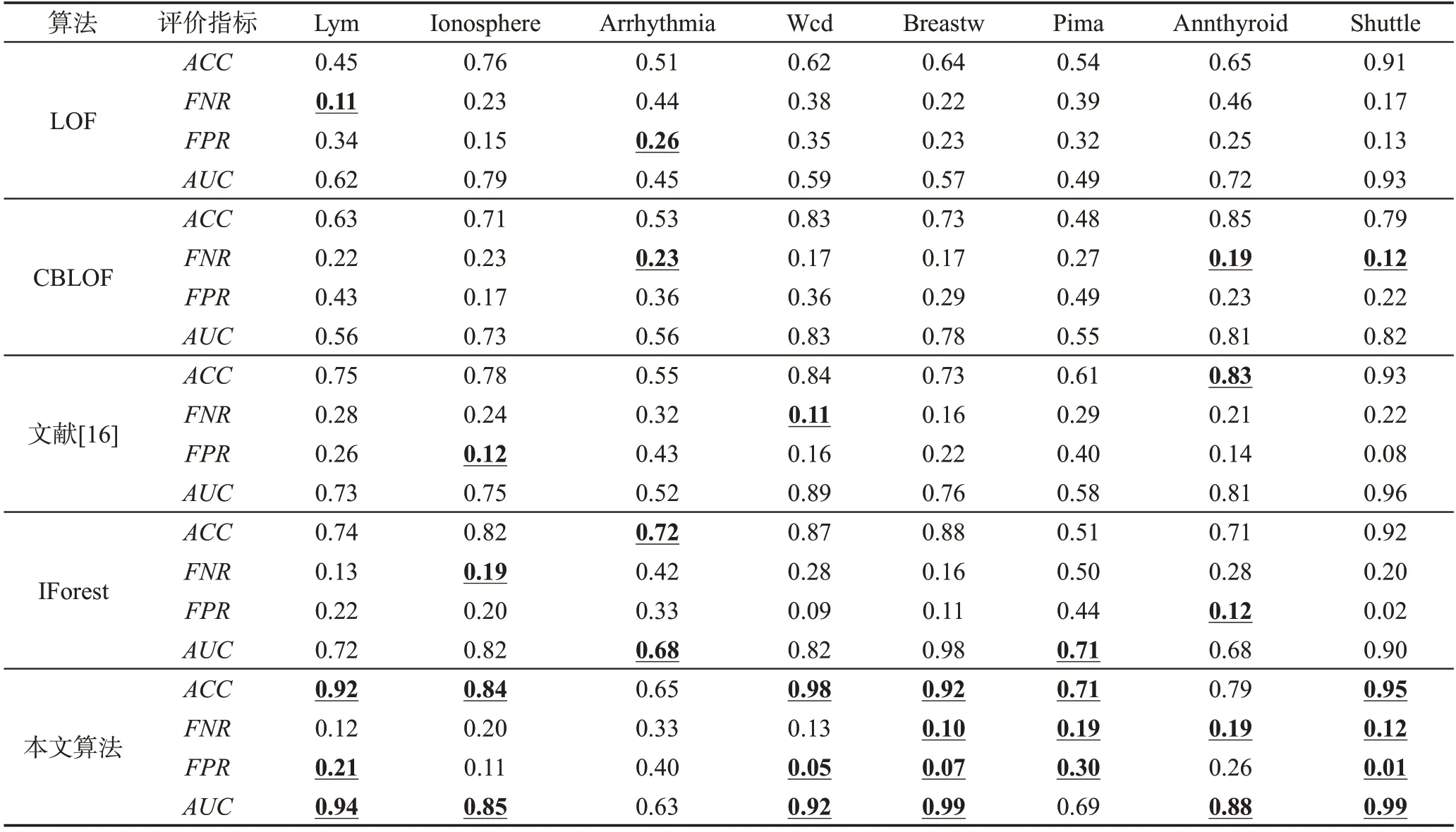
Table 2 Comparison of experimental results by different algorithms表2 不同算法实验结果对比

Table 3 Parameter setting information表3 参数设置信息

从表2中的对比实验结果可以看出，除了Arrhythmia和Annthyroid数据集之外，基于高斯核密度估计的异常值检测方法相对于4个对比算法对其余6个数据集具有更高的检测准确率。其AUC值也仅在Arrhythmia和Pima数据集上低于其他算法。其中，在Wcd 数据集上，检测准确率达到了98%，远高于IForest 的87%。在Breastw 数据集上，本文算法的4个检测指标都优于对比算法，且AUC值达到了最高的0.99。当数据集较小时（Lym），AUC值达到了0.94，准确率为92%，大幅高于其他算法，同时假正率也是最低的；当数据集维度较高时（Arrhythmia），虽然其AUC值不是最高的，但与由IForest 算法取得的最高值0.68接近，且针对此数据集，5个对比算法检测效果都不理想。在数据集较大的情况下，本文方法的优势也远远大于其他几种算法，例如在Shuttle数据集上，准确率为95%，远远高于CBLOF算法的79%。

以上实验表明，在经过t-SNE 算法提取特征后，能够增强样本间的局部结构能力，解决高维空间中样本稀疏问题。通过高斯核函数对LOF算法进行改进，能够大幅提高检测准确率。

4.2 健康数据异常检测结果

在验证了算法的性能后，利用该算法在采集到的手环健康数据集上进行实验，找出异常值。图4是将数据集经过特征提取后，采用本文GKDELOF算法进行异常检测的结果。其中白色点表示正常数据，红色点表示异常数据。

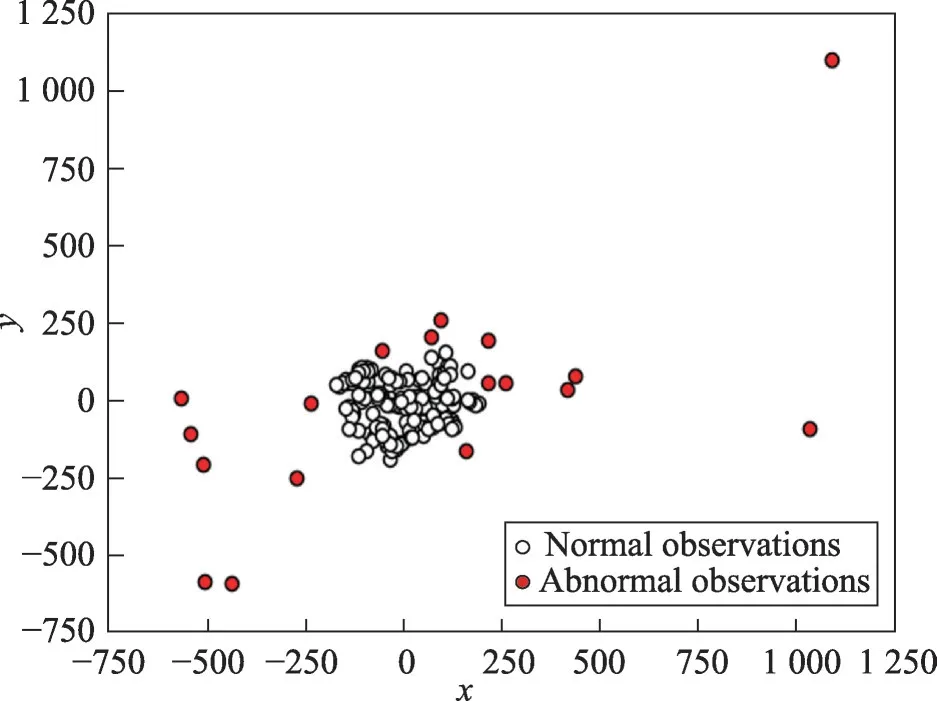
Fig.4 Outlier detection result by GKDELOF on health data图4 GKDELOF算法在健康数据上离群检测实验结果

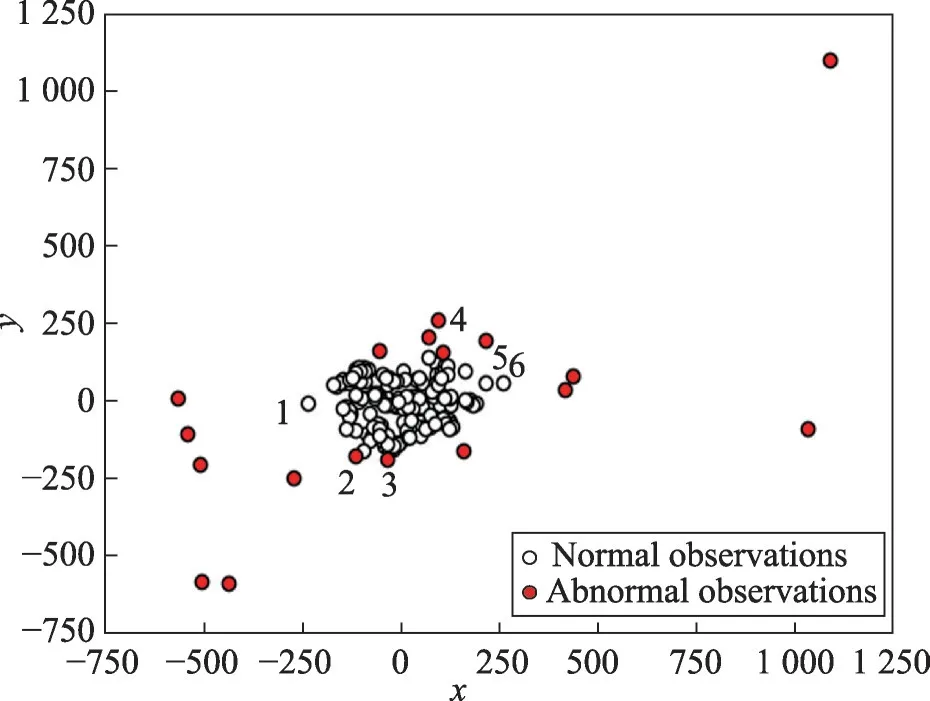
Fig.5 Outlier detection result by IForest on health data图5 IForest算法在健康数据上离群检测实验结果

为验证本文算法的优势，图5为利用检测效果仅次于本文算法的IForest算法在同一健康数据集上进行异常检测的实验结果。对比图4和图5可以看出，两种方法对于明显的离群样本点都可以检测出来，但IForest算法在簇群边缘处存在漏判和误判。标号为1、5、6的样本点为漏判，标号为2、3、4的样本点为误判。而本文算法在检测簇边缘离群点时，未存在明显漏判或误判情况。

5 结束语

本文针对智能穿戴设备普及背景下，利用运动手环采集的活动数据存在未知异常数据的问题，提出一种基于高斯核密度估计的健康数据异常值检测方法。该方法在利用t-SNE算法进行特征提取，增强局部结构能力的基础上，通过高斯核函数改进LOF算法，提出基于高斯核密度估计离群因子算法，该方法的判定阈值较为稳定。在实验部分，利用异常检测具有代表性的标准数据集进行实验，验证了特征提取的作用；并且对比了其他4种异常检测算法，实验结果表明，该方法具有较好的检测效果。最后，利用该方法在真实数据集上找出异常值。

在数据预处理方面，选取的特征指标是否能够有效地表现数据特征在一定程度上会影响检测的准确率，因此还可以从数据特征指标选择方面做进一步研究。