移动APP演化模式分析与预测*

张艺璇，郭 斌，欧阳逸，王 柱，於志文

西北工业大学 计算机学院，西安 710072

1 引言

1.1 研究背景

移动APP 自推出以来就飞速影响着人们的生活。随着其数量的爆炸式增长，软件开发商需要根据市场反馈及时做出运营决策，广告投放商更需要通过预判抓住转瞬即逝的商机。显然，如果各种类型APP的流行度演化过程以及其未来一段时间内的预期表现能够被开发商和广告商事先得知，则可为相关决策提供十分有价值的信息。本文中流行度演化是指APP的受欢迎程度在时间轴上的流动与变化过程。如果能够对演化过程进行合理分析与预测，就能够为软件开发商管理和更新APP 提供决策建议，切实提高消费者的使用体验，从而逐渐实现APP的智能演化；长远来看，这有利于应用软件市场的细分与优化，最终导致市场整合，带来极大的应用和商业价值。

然而，流行度动态演变迅速，其背后各种因素交织作用，很难完成单独量化。现有APP 流行度相关研究可大致概括为以下三方面：

一部分研究[1-2]通过分析促进APP发展的积极属性来构建预测模型，或通过分类预测用户下一个应用的APP。这样方便分析和理解APP的发展过程，但不同种类、不同排名的APP所受影响因素不同，仅仅依靠影响因素对APP流行度进行预测不具有通用性。

另一部分研究[3-5]侧重从APP早期流行度出发建立回归方程或者采用分类算法预测流行度，针对时态模式的组成预测APP流行度发展。这种方法在预测近期流行度时具有较高准确度，但当预测时间延长时则表现不佳。另外，这样预测流行度时效性不强，必须等待历史流行度数据出来后才能进行预测。

此外，由于APP市场庞大，各类使用数据种类众多且十分复杂[6-7]，预测工作不应只获得预期流行度，还应针对流行度演化过程给出合理分析和解释。

1.2 研究问题

为了全面考虑早期流行度、影响特征对APP 的影响，本文针对流行度演化的分析、预测，主要研究以下3个问题：

（1）APP 流行度演化过程中是否存在一些共性模式？

APP 流行度的演化过程通过APP 每日流行度的拟合曲线表示，其中流行度以每日下载量量化，演化中必然存在大量上升与下降过程[8]。如果能够将上升与下降合理切割归类为演化模式，就能把复杂无规律的APP 演化量化为某些模式的组合，这些模式分别对应不同的含义和意义。这直接有助于判断APP 的生命状态、当前受制约因素和未来改进的方向；从逆向工程的角度而言，这项研究能够对APP进行实时监测，考查APP各项指标的异常情况，从而更加精准地决策当前最佳更新或营销活动，而不是仅仅为了提高产品在APP 市场中的曝光率而盲目更新。这项工作直接与未来的预测息息相关。

（2）如何找到并量化流行度的影响因素，如何衡量它们的影响作用？

APP的自身特性、同类产品间的竞争情况以及用户对于APP使用感受的反馈等因素都直接影响APP的流行度，如果能够量化对应这3类影响因素的具体特征指标，并结合得到的演化模式进行分析，就能得知是怎样的组合导致了某一时刻APP 的流行度表现。一旦找到影响流行度的因素并量化其影响力大小，便能够针对表现不佳的影响因素提出改进策略。

（3）如何针对影响特征建立模型以预测流行度的演化趋势？

当获得APP流行度的影响因素及其权重便可建立数学模型以预测未来一段时间内APP的受欢迎程度。这项工作有助于软件开发商针对自身APP未来预计表现及时作出决策，提高用户体验；同时，它对APP市场整合和智能演化均有帮助。

1.3 研究成果

针对以上3个问题，本文得到如下成果：

（1）发现了7种流行度演化的原子结构，并通过序列模式挖掘发现了6类演化模式。

执行曲线切割算法后，针对曲线形状进行聚类，最终得到不同状态下的7种原子演化结构，它们均代表APP流行度的上升或者下降的单个过程。之后针对APP为期一年的流行度演化原子结构进行序列模式挖掘来将上升与下降的原子结合得到6类演化模式。后文将针对不同的演化模式分别给出定义、特征、出现时期、意义等详细表述。

（2）选择出6种与APP流行度演化相关的特征并对其作用进行了详细分析。

通过对获取数据的分析并参考已有文献中特征的选取，本文归纳6种作用于APP 流行度表现特征，它们归类为以下三方面：自身特性（版本更新、营销活动等）、同类竞争（实时排名等）、市场反馈（评论量、评分和评论情感等）。后文给出各种特征的解释说明，从而证实选取该特征的正确性。

（3）结合分析内容建立CrowdPop 预测模型，通过更加细粒度地结合历史表现与特征因素，实现了对APP流行度演化的准确预测。

本文提出一个综合考虑APP历史演化模式与日常特征因素的CrowdPop 预测模型，并根据实验结果通过不断优化演化模式的量化方法从而提高预测模型的准确性。实验设计包括4类特征作为预测因子的CrowdPop模型基准研究和8类特征作为预测因子的CrowdPop 模型，通过最小化测试集与预测集间均方误差选取最优的改进模型，并与另外两种算法进行预测精度的对比，从而验证了成果（2）中有关APP演化模式的分析结果，从而证实了分析和模型的准确性与实用性。

与现有工作相比，CrowdPop 模型综合考虑了历史流行度与影响特征对APP 未来流行度的影响，并且随着预测时间的延长，该模型均表现出较好的准确性，克服了现有研究中长远流行度预测准确率不能保证以及忽略历史流行度的影响等问题。

2 相关工作

2.1 APP流行度的影响因素

目前国内外学者针对移动APP流行度的影响因素开展了系列研究。Lee[9]提出并分析了对移动APP的可持续性产生积极影响的若干属性，并提出一种选取有效特征的方法，为本文选取影响特征提供了思路。Liu 等人[10]通过分析应用程序的用户行为数据，获得多个应用程序管理活动和应用程序使用模式。Guzman 等人[11]提出了一种自动化方法，可帮助开发人员过滤、汇总和分析用户评论。它可以帮助开发人员系统地分析用户对单个功能的意见并过滤不相关的评论。Sarro等人[12]介绍了应用商店中APP生命周期的理论特征，他们的分析还突出了价格、评级和受欢迎程度之间的关联。Tian等人[13]从1 492个高评级和低评级APP案例研究中提取最有影响力的因素，并应用随机森林分类器来识别高评级应用。Arzt 等人[14]提出了一种基于用户行为来衡量应用相似性的新技术。他们采用信息检索来提取特征并将其用作APP的表征，然后使用这些属性来聚类APP。

2.2 流行度建模与预测

现有预测工作中，针对网络信息或者线上内容的研究最为成熟，它们针对时序化的流行度建模，流行度定义为某时刻发生的积极网络动作的次数。现有研究工作从预测方法的角度可以分为3类：基于早期流行度、基于影响流行度的因素和级联传播理论。Zhu 等人[15]提出一种基于隐马尔可夫模型的顺序方法，用于对移动APP 的流行度信息进行建模。Lu 等人[16]提出了一种捕获用户行为的方法，包括APP下载和安装、卸载和用户评级。通过用户行为与开发人员可控属性相结合来预测APP 未来使用率。斯坦福大学的Yang等人[17]提出了一个有效的时间序列聚类算法以研究线上内容随时间变化的模式。Cha 等人[18]通过研究发现网络信息中早期流行度与未来流行度存在较强关系，由此该研究以早期流行度作为预测因子建立回归方程开展预测工作。Hong等人[19]将经典的一元回归SH（Szabo-Huberman）模型扩展至多元，针对历史流行度分配不同权重，以最小化平均相对平方误差为目的训练模型。Bandari等人[20]针对时效性较强的新闻信息定义4个特征并将其作为自变量，未来流行度作为因变量并建立对数回归方程，相比早期流行度对时效型信息预测的不准确性而大幅度提高模型的预测性能。许多现有的预测模型对于短期预测具有良好的准确性，但当用于长期预测时性能变差。

以上工作为本文研究APP流行度预测提供了思路。本文同时考虑影响因素与早期流行度对APP未来一段时间的流行性的影响，并针对早期流行度挖掘出6种演化模式。之后建立预测模型CrowdPop，将选定的因素和模式量化为8种预测因子用作模型输入。实验表明，与基准研究相比，CrowdPop在预测精度上获得相对更好的性能。另外，本文提出的6种演化模式为后续研究人员在理解APP流行度演化的过程中奠定良好基础。

3 数据收集与预处理

3.1 问题表述与分析

现有预测工作中，针对网络信息或者线上内容的研究最为成熟，它们针对时序化的流行度建模，流行度定义为某时刻发生的积极网络动作的次数。

为了统一概念与符号，方便理解内容，本节针对第1章中提出的研究中3个基本问题的相关概念和理论进行形式化描述和说明。

（1）流行度：给定某个APPi和时间点t，流行度pi(t)定义为其在时刻t的受欢迎程度。本文选取APP当日下载量来量化APP当日流行度。下载量能够较好地反映用户对于APP的喜爱程度。

（2）流行度演化：给定某个APPi和生命长度Li，流行度演化定义为时间序列{pi(1),pi(2),…,pi(Li)}。通过以一天为时序单位，以一年时间跨度的每日下载量曲线来模拟APP 流行度一年内的变化情况，探寻影响流行度变化的因素和流行度的变化特征。

通过对APP 的流行度演化的基本观察与分析，本文提出3类与流行度紧密相关的指标：自身特性、同类竞争和用户反馈。这3类指标分别由以下特征进行量化。

（1）自身特性

①版本更新

软件开发商会不定时推出软件的更新版本供用户下载使用。更新动作从短期来看能够有效提高APP在应用市场中的活跃度和曝光率，提高潜在用户的安装率；长远来看更新动作实现了对软件性能的优化，能够稳定已有用户群体并吸引潜在用户使用。

②营销活动

开发商会不定时推出一系列线上或者线下的营销活动来提高APP的关注度。良好的营销活动能够有效提高用户体验，增加用户粘度，有助于潜在用户的积极转化。

（2）同类竞争

①实时排名

本文利用日下载量数据中最近一天的APP市场排名作为APP 的流行度排名，用于观察随流行度下降演化模式的变化情况。同时，实时排名符合“富者更富”思想，即当前十分流行的APP未来会更有可能被潜在用户知晓并安装使用。

②同类APP数量

尽管市场排名能够很好代表某APP在同类产品中的受欢迎程度，但是同类APP 数量更能反映子市场竞争的激烈程度。这里统计同类APP 的数量，用于日后观测某类型对应子市场的发展情况。

（3）用户反馈

评论量、评分和评论情感：开发商往往采取评论有奖、APP 弹窗等措施来鼓励用户积极评论以促进APP的完善。本文将用户评论划分为三部分，评论量、评分和评论情感。评论量在一定程度上能够表征用户对于APP使用感受发表意见的积极程度。评分是用户对于APP最直观的感受，十分直观但不够细致。评论情感是针对评论内容进行文本分析得到的文本情感评分，更加具体地反映了用户对APP的喜爱程度。

3.2 数据收集与描述

本文收集了来自酷传网站（http://www.kuchuan.com）的多源群智APP 数据，涵盖360、百度、应用宝、豌豆荚等10个在中国广受欢迎的APP市场，涉及APP单日下载量、日均使用时间、实时排名、用户评论等多类时序和文本数据。数据集相关信息如表1所示。

3.3 数据预处理

首先针对采集数据进行初步筛选，选取各项指标均不为空的APP，并参考APP市场中的分类对APP分类和整合；之后对上述特征数据进行预处理得到各项时序数据。不同类型的数据的处理方式如下。

（1）日下载量：首先对日下载量进行归一化，之后采用Matlab 的工具箱进行曲线拟合，从而得到贴近真实演化过程的平滑曲线。

（2）版本更新与营销活动：这两者处理为0/1结构，即当天有更新发生则数值记为1，反之为0；当天有营销活动则记为1，反之为0。这样就相当于间接给有更新和营销活动的日期标注，方便日后分析当日APP流行度所受的影响因素。

（3）实时排名：针对每一类APP进行实时排名的升序排列。存在一种情况：部分排名在中段的APP因数据类型不全而被剔除，注意更新排名的数字。

（4）同类APP数量：通过统计每种类型中APP的个数来得到同类APP 的数量，用于日后结合实时排名进行关乎市场竞争的综合判断。

（5）评论量：针对获取的每日评论进行计数，用数值大小来代表当日用户评论的活跃情况。

（6）评分：用户切换至APP市场的评论界面时可以对APP直接打分。假设没有用户恶意评论的情况，直接对每日评分求平均值，这个平均值代表当日该APP获得的评分。最后针对一年的评分做归一化处理。

（7）评论情感：本文采用SnowNLP（https://github.com/isnowfy/snownlp）计算评论的情感得分。SnowNLP是用于切割识别中文短语的Python 语言类库，用来对评论量化生成情感评分。在计算每日评论情感得分的平均值后针对一年的数据进行归一化。

4 移动APP流行度分析

本章通过对APP一年时间内流行度演化的过程进行统计和分析，旨在发现流行度演化的基本原子结构，挖掘频繁序列模式并探究演化发展的规律及其背后的原因。

4.1 原子结构

本文采用APP的日下载量来刻画APP在用户市场中的流行程度，以每日时间点作为横坐标，每日下载量作为纵坐标的取值。这里给出原子结构的形式化定义。

原子结构：给定某APP的流行度演化曲线，原子演化结构是其中一段由相邻连续坐标点组成的整体符合单调增或减的二维序列，保证序列在维持原有增减性下的最大化。增减过程中允许出现若干小型波动，但波动处的差值不能超过序列首尾纵向差值的θ（0 ＜θ＜1）。

下面对以上定义进行解释。APP 流行度演化整体符合上升-下降模式，但允许在上升或者下降过程中出现并不影响整体走势的波动。这些波动可能是因为APP的连续更新动作导致流行度迎来持续的脉冲式增长（对应波动式增长原子），也有可能是因为更新后APP的不稳定性导致用户评分走低从而流失部分潜在用户（对应波动式下降原子），具体原因将在第5章给出。但并不代表只要存在波峰或者波谷就应该被划分为不同子序列，这样做可能会破坏在升降中出现的异常。

下面给出切割算法。

算法1演化曲线切割算法

输入：流行度演化序列和生命周期时间序列。

输出：流行度单调子序列集合。

1.读取流行度波峰值和波谷值；

2.分别读取波峰值，划分振幅阈值内的邻居点作为上升子序列；

3.保存上述序列至单调增序列集合中；

4.分别读取波谷值，划分振幅阈值内的邻居点作为下降子序列；

5.保存上述序列至单调降序列集合中；

6.输出两个单调子序列集合；

7.结束。

针对APP 流行度拟合曲线切割后，得到对应时序数据的原子结构序列。针对原子结构进行聚类时，本文采用K-means 聚类算法（https://github.com/skyline0623/K-meansCluster），这是一种通过计算欧氏距离来寻找聚类中心点的迭代算法，由于移动APP数据之间差别很大，上升和下降情况十分复杂，聚类并不局限于增降过程的速率。聚类后得到并定义7种原子结构，结果如图1所示。其中原子结构A2和A4表示上升和下降环节中存在一个或多个小型的波峰或波谷，图中一律使用一个波折段表示。A5和A6表征了更新动作发生时下载量尖峰式的脉冲。A7表示了较长一段时间内APP流行性维持平稳状态波动很小的状态。

Fig.1 APP popularity atomic evolution structure图1 APP流行度原子演化结构

4.2 序列模式挖掘

本文采用APP的日下载量来刻画APP在用户市场中的流行程度，以每日时间点作为横坐标，每日下载量作为纵坐标的取值。这里给出原子结构的形式化定义。

由于APP 的流行演化基本遵循上升-下降的过程，因此本文针对得到的原子结构序列进行相邻奇偶位置组合统计，筛选高频出现的原子结构对归纳为演化模式，共得到6个不同类型的组合即流行度演化模式，结果如图2所示。

Fig.2 APP popularity evolution pattern图2 APP流行度演化模式

（1）P1模式

这种模式最为常见，是最主流的APP演化模式，在绝大多数APP 的生命周期中均会存在。P1代表一种相对稳定的流行度变化状态。它表征APP在发展过程中受到某些内部或者外部刺激时，其流行度产生相对稳定的应激反应。其中的上升与下降过程均为幂律消长状态。整个过程可理解为，流行度上升过程中未受到消极因素影响而阻碍正常进度，下降过程也符合幂律型自然发展规律，未受到人为干预或干预较小。

（2）P2模式

这种模式是继P1后较常见模式之一，流行度的下降过程仍遵循幂律形式，但上升中存在一个及以上的中断或者波动，流行度的增长受到一定内部或外部阻碍。本文认为中间的波动存在两种可能：正常增长过程受到内部或外部影响因素的阻碍而减缓增长速度；增长处于瓶颈状态因采取一定措施（连续更新或者营销活动）而挽回一定的增加量。

（3）P3模式

这种模式是继P1之后另一种较为常见的模式，其流行度上升过程遵循幂律形式，但在下降过程中存在一个及以上的中断或者波动，流行度的降低受到一定内部或者外部的积极刺激而产生正向反馈。中间的波动存在两种可能：正常下降过程受到内部或外部的积极影响，例如开发商的一系列有效动作等，从而在流行度下降的中段位置维持了一段时间的稳定水平；某些导致流行度下降的不利因素级联式地扩大，从而牵连至原本较为稳定的用户群体。

（4）P4模式

P4是一种不常见的模式，其上升和下降阶段中都存在若干波动，但整体仍呈幂律走势。导致P4的原因较为复杂，两个阶段的波动除受上述评论、更新等因素影响外，可能还存在其他组合因素的影响。整体而言，演化模式P4代表APP受内外部因素影响后波动最为复杂，稳定性较差，尚未形成自身的发展规律。

（5）P5模式

P5代表存在更新动作时APP 流行度演化的模式。本文将更新动作发生的前一天作为第一个数据点，以完整表现更新动作对APP 流行度的巨大影响。由于使用下载量量化APP 流行度，因此大量已经安装此APP的用户可能会选择更新，从而P5会显示出急速的上升和下降。

（6）P6模式

P6被定义为连续7天及以上只发生微小变化的情况。事实上，数据统计显示大多数情况下一段时间内的下载量趋于零。因为流行度演化通常是遵循上升、下降的模式，所以这是一种异常的演化模式。排除数据采集出现的缺失，这可能是APP 流行度演化中较为严重的瓶颈期，大多存在于流行度排名较差的APP中。

4.3 演化模式分析

针对不同APP 的频繁模式序列，本文进行了数量、频率、类别、排名等不同方面的统计工作，并从统计结果中分析得到了系列论点以及论点的合理解释。由于P5和P6代表特殊情况的演化模式，因此本文暂不考虑。

4.3.1 生命周期中的演化模式数量

演化模式P1在各类APP 的生命周期中大量存在，是最为常见的演化模式，因此P1的数量可用于刻画大部分APP 生命周期中演化模式的整体数量。另外，由于数据时间跨度较长，因此某类演化模式出现数量的多少在一定程度上可以反映这类演化模式出现的频率。

P2与P3属于较为常见的演化模式，其中大多数类别的APP 的生命周期中P3的出现次数较P2多。这是由于APP 市场本身并不稳定，内外部影响因素繁多复杂，APP 的流行度增长的原因较为清晰，但导致下降的因素较为复杂多变，这也是APP 市场波动频繁剧烈的因素之一。

P4是这4类中出现次数最少的演化模式，它代表着APP的不稳定状态，受内部外部影响变化剧烈，但这种不稳定状态并不常见。

4.3.2 不同演化模式的占比

不同模式所占百分比情况如图3所示。

P1在各类APP中的出现次数均达到整体模式的43%以上，是所有APP中的主流模式。

P2与P3所占百分比浮动较大，但其加和不超过P1所占百分比。P2与P3的比重变化更多受APP所属类别以及该类市场发展情况的影响。

Fig.3 Percentage of 4 evolution patterns图3 4种演化模式出现次数所占百分比

P4所占百分比浮动不大，一般在5.50%左右。

4.3.3 不同流行度之间的演化模式差异

这里根据APP的市场排名对不同APP的流行度进行排名，考察当流行度逐渐下降时演化模式的不同表现。

（1）演化模式数量差异明显

随着APP 流行度的下降，演化模式数量出现一定规律的波动，波动情况如图4所示。其中位于流行度排名中上段和中后段的APP 其模式数量较大，具体为25.0%左右与80%左右。

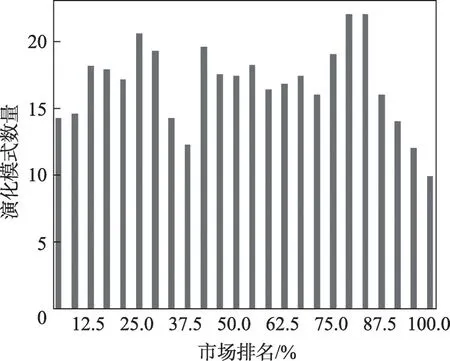
Fig.4 The number of 4 patterns as APP ranks down图4 随APP排名下降4种演化模式出现次数

分析认为排名在25.0%左右的APP 正处于加速上升的竞争阶段，这期间开发商更新动作频繁，流行度变化速度加快，因此演化模式数量在该类APP 中占据高点。

分析认为排名在79.2%左右的APP 用户群体较小，APP 的流行度发展远远未到达稳定状态，受内外部冲击后波动幅度频繁且剧烈，因此演化模式数量明显大于其他排名的APP。

排名理想的APP多属于行业巨头，其发展稳定，更新动作规律，评论真实性较高，具有稳定的用户群体，因此受内部、外部影响波动小。

（2）演化模式占比变化较大

随着流行度的下降，演化模式P1所占比例在逐步下降，演化模式P2、P3、P4都有不同幅度的波动且总体呈上升趋势，这证明随流行度下降，APP 发展所受影响因素增多，波动增多，常见的稳态模式逐渐减少，富于波动的模式的出现更加频繁。

（3）演化模式的活跃位置不同

这里以演化模式出现的百分比量化该演化模式的活跃度。在生命周期中，演化模式出现百分比越大，则证明当前时期该演化模式越活跃。不同模式在APP排名中活跃位置如图5所示。

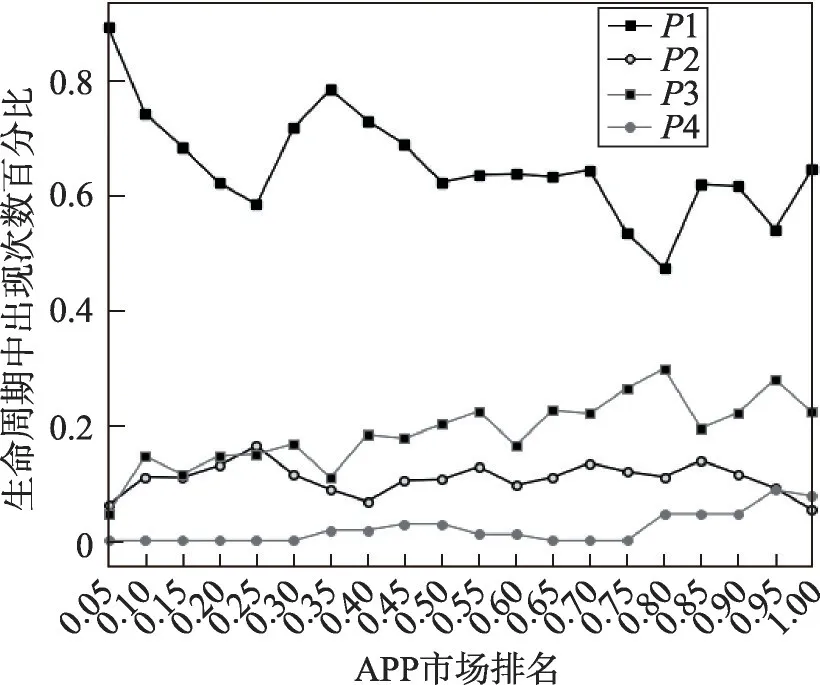
Fig.5 Active position with 4 patterns as APP ranks down图5 随APP排名下降4种演化模式的活跃位置

P1在整个生命周期中都十分活跃，但随着流行度的下降，演化模式P1的活跃度整体呈下降趋势。排名在50%左右的APP 是演化模式P1占比下降的分水岭，前后两阶段的APP 的演化模式P1出现的百分比差异较大。

P2的最活跃期出现在25%左右，说明对于流行度增长速度表现强劲的APP，P2是它们最受欢迎的模式，这既代表开发商对于增长的努力，也代表未来发展良好的能力。当然这也与APP 发展现状相吻合，同行竞争大，流行度上升难，但APP稳定性强，因此需要采取措施不断提高流行度增长的速度。

P3的最活跃期出现在70%左右，大多出现在排名的中后段位置，说明流行性表现不佳的APP 在针对降低下降速度而做出努力，此处开发商的关注点可能已转移到如何减小损失，降低每次下降的速率。这也与APP 发展现状相吻合，来自相同位次的同行间竞争较小，流行度上升较为容易，但APP发展的稳定性差，因此需要不断采取措施减缓流行度下降的速度。P2与P3的活跃位置还受其他因素影响。

P4因出现数量较少无法得到确切的规律，但可以看出其多活跃于排名中后段的APP 的生命周期中。说明流行度排名较为优越的APP很难出现上升下降过程中都包含曲折过程的演化模式，当排名不佳时，其演化过程更为复杂，所受影响因素更多，更加不稳定。

4.3.4 演化模式平均持续时间的差异

并非是TOP APP 就一定稳定，它们的每一次更新影响深远，波及用户人数多，演化模式持续时间较短但演化模式种类较为单一。

排名中上段较为稳定，演化模式持续时间较长，种类开始增多，上升需要更多助力，主要精力放在增加下载量上。中下段不是非常稳定，演化模式持续时间短，变化多，开发商动作频繁但影响并不深远，主要精力放在减慢下降速度上。最后段表现不佳，变化多但可能更多是受外部影响，稳定性差。根据统计计算，演化模式的平均持续时间如表2所示。

Table 2 Average duration of each pattern表2 演化模式平均持续时间

5 APP流行度预测方法

5.1 CrowdPop预测模型架构

本文提出基于随机森林（random forest，RF）的CrowdPop 预测模型，将深远影响APP 流行度的8种特征作为预测因子输入，通过训练21天（第1至3周）的APP数据来预测后7天（第4周）的APP流行度。采用MSE（mean square error）与RMSE（root mean square error）来验证模型的准确性。为了进行对比，采用多元线性回归（linear regression，LR）和支持向量机回归（support vector regression，SVR）两种算法作为参考基准。CrowdPop模型架构如图6所示。

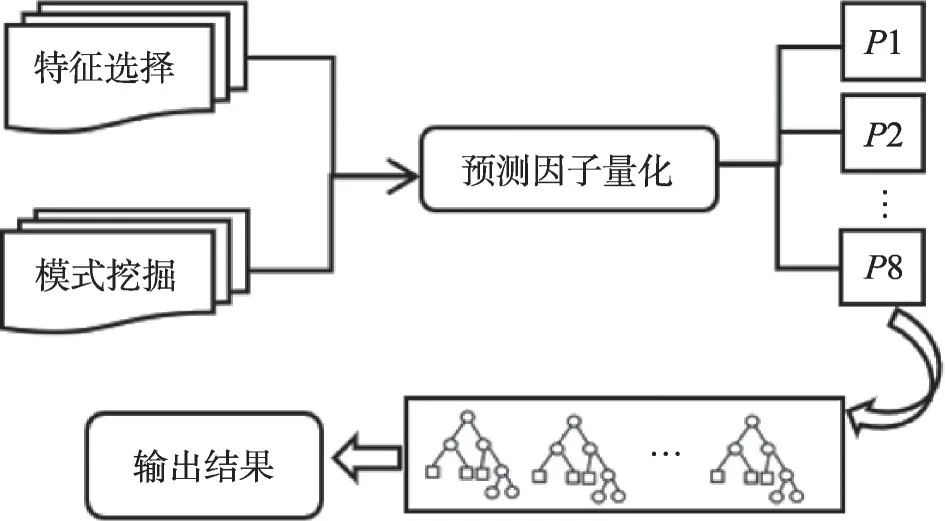
Fig.6 CrowdPop model architecture图6 CrowdPop模型架构

5.2 CrowdPop预测因子

CrowdPop 模型的预测因子包括P1、P2、P3和P4的表现、评论量、评分、评论情感、更新动作，需要将其量化为8种时序数据作为CrowdPop模型输入。

为方便区分，将APP 的更新频率、评论量、评分和评论情感这4种特征称为显式特征，因为其源于APP的维护运营和用户反馈中；对应的隐式特征是包含APP生命周期中流行度演化过程反映出的演化模式组成、持续时间等特征信息。

为了更加显著地表现出CrowdPop 模型的优越性，实现演化模式组成这一预测因子的最佳量化，本节共提出4种表示隐式特征的方法，分别为：

方法1当天演化模式占比序列

即当前时间内所处演化模式的类型。这里数据采用稀疏矩阵的表示方法，每行4个状态中仅有一个状态取值为1，代表当前正处于这类演化模式的过程中。

方法2叠加式演化模式占比序列

考虑到演化模式并不只是作用于相邻的有限时间内，方法2将针对方法1中的稀疏矩阵进行纵向叠加，叠加后每行数据代表截止到当天，之前出现的所有演化模式的组合情况。

方法3叠加式持续时间序列

参考本文在4.3.4小节中得到的结论即不同演化模式的持续时间差别较大，考虑到仅仅标记演化模式的出现并不能准确刻画出不同模式在APP流行度演化过程中的持续性，这里提出方法3，将矩阵表示为直至当天时间，之前出现的各演化模式的持续时间的叠加，不同演化模式的出现频率不同，出现次序不同，其持续时间也不同，方法3更加细化了演化模式对于未来流行度的影响和作用。

方法4时间窗口式持续时间序列

设置时间窗口滑动机制，通过改变窗口长度来确定叠加的时间长度，矩阵数据仍表示为持续时间的叠加，但不直接设定为截至当天出现的所有演化模式的持续时间。

CrowdPop模型分别采用以上4种方法作为输入并依次计算不同方法下CrowdPop 模型的预测精度，最终发现方法4作为最佳输入有效优化了基准研究的预测精度。实验输出为模型中的各概率初始参数，预测周的平均下载量和预测周的流行度演化曲线。

5.3 CrowdPop预测算法

CrowdPop 模型采用随机森林RF 算法对输入的预测因子进行APP未来一段时间内流行度的预测工作。之后分别与多元线性回归LR、支持向量机回归SVR算法的预测精度进行对比，以验证CrowdPop模型在预测算法方面的优越性。首先对RF算法进行简要介绍。

随机森林是一种多功能机器学习算法，能够执行回归和分类的任务。在APP流行度的预测工作中，随机森林算法主要从以下步骤完成回归预测工作：

（1）针对训练集生成多个决策树并组成决策森林；

（2）基于APP 的8种特征数据进行未来流行度的预估；

（3）随机森林中的每一棵树都会给出自身的分类输出值；

（4）森林整体将所有决策树输出的平均值作为输出结果，即对应当前特征取值的APP一周下载量。

另外本文引入多元线性回归与支持向量机回归两种算法与CrowdPop模型进行对比，下面分别对LR和SVR进行简要介绍。

（1）LR算法

多元线性回归算法用于刻画与APP流行度演化相关的8个自变量与APP未来流行度间的线性关系。通过LR算法建立训练集中7天前特征的取值与当前流行度的线性关系，并得到不同特征的权重参数，以便实现通过当前特征取值预测未来流行度的工作。

（2）SVR算法

SVR 算法本质为寻找一个回归平面，让一个集合的所有数据到该平面的距离最近。它从训练集数据中选取一部分更加有效的支持向量，根据这些训练样本的值通过回归分析预测对应当前特征数据取值的未来一段时间APP流行度的取值。

6 实验验证

预处理的数据包括7个功能分类共126个APP，每4周为一组数据，共计6 148组。其中每组数据包括21天（3周）的训练数据和7天（1周）的测试数据。

6.1 实验设置

为了更加清晰地对比CrowdPop模型结合4种不同量化方法的预测精度，以及引入P1、P2、P3和P4这一隐式特征对于APP 流行度预测的必要性，本节设置基准方法，实现结果的清晰对照。这里仍采用CrowdPop 预测模型架构，但只引入除去演化模式的其他4类影响因子：评论量、评分、评论情感和更新动作。并将预测结果的MSE 与RMSE 作为对比基准。在增加演化模式组成与持续时间这一影响特征后，通过比较不同方法的MSE与基准方法MSE的大小，从而判断不同方法下CrowdPop 模型针对APP 流行度预测的性能差异，选取最优模型与方法。

首先建立4类显式特征与APP 流行度间的数学关系。分别采用LR、RF和SVR算法针对显式特征与APP流行度之间建立数学关系，计算对应测试集的预测数据集，并计算测试集与预测集的MSE和RMSE，统计针对每个APP 产生最小MSE 值的算法，结果如表3所示。

其中，最优百分比表示这种算法在针对同一APP进行预测时，相比其他两种方法，其MSE 值最小，即预测准确性最优。可以看出，LR 与RF 在这6 148组数据中的表现平分秋色，MSE 的均值也在同一数量级上，相差较小。而SVR在预测精度上则表现不佳，其MSE值与RF相差一个数量级，当对同一APP进行预测时，更是很难表现绝对优势。因此下一步实验摒弃SVR算法，采用LR与RF进行性能对比。

Table 3 Accuracy comparison of predictive algorithm表3 预测算法精度对比

6.2 实验结果

方法1当天演化模式占比序列

这里采用稀疏矩阵表示，通过0或1来代表当天流行度处于何种演化模式。设置为4×365的稀疏矩阵，其中行值代表时间序列，列值表征4种演化模式在某一天的取值，当天如果正处于演化模式P2，则该天P2特征值取值为1，P1、P3和P4特征值取值为0。从横向的角度看，P1、P2、P3和P4的取值构成了4个隐式特征，0/1取值反映当天APP 所处演化模式的状态。从纵向来看只研究一周前的同一时间APP所处演化模式对于当下流行度的影响，实际上可以理解为历史流行度对于当前流行度如何演化的影响。将演化模式序列与其他4个显式特征对应组合后，应用LR 和RF 两种算法分别对APP 的一周流行度进行预测和计算MSE，并将实验结果与6.1节中对应数据的MSE 比较，从而发现方法1对于预测模型的优化情况。其中优化结果如表4所示。

Table 4 Method 1 optimization表4 方法1优化情况

隐式特征的引入能切实提高模型的预测精度，但是并不能实现对所有实验集的优化，排除APP 个体差异，有理由认为只是反映当前APP 演化模式的状态并不能完全涵盖演化模式中蕴含的信息。例如一个APP如果连续处于多个P1模式中，那么在一段时间内其隐式特征取值就不会改变，如果考虑演化模式的出现对于未来APP 流行度演化的叠加式效应，模型的预测精度是否会进一步提升呢？

方法2叠加式演化模式占比序列

引入隐式特征的叠加式数据来探究其对APP流行度演化的影响和对模型的优化。具体为实现方法1中代表4个隐式特征的稀疏矩阵进行纵向的叠加，即当前隐式特征仍表示为4×365的数值矩阵，但每一个数值代表截止到当前时间，之前出现过某种演化模式的次数。在对模型进行进一步的改进之后将实验结果继续与基准研究对比，对比结果如表5所示。

Table 5 Method 2 optimization表5 方法2优化情况

实验结果显示方法2针对基准研究优化范围十分有限，即当引入演化模式在时间推移上的叠加式影响时，模型的准确性并没有得到预期效果。为此本文分析方法2得到的各个特征数据的平均参数，并与基准研究中4个显式特征的参数进行对比。对比结果如图7所示。对比发现，显式特征在不同模型中的变化并不显著，针对不同APP 进行预测时其值在正常范围内波动。图7展现了在基准研究和方法2中采用特征不同但显式特征参数近似的情况。之后统计所有样本集P1、P2、P3和P4这4个隐式特征的参数并求取平均值，结果如表6所示。

各演化模式表现在方法2模型中的参数值依次递减，其中P2至P4和P1对应的参数相差4个数量级。模型不够合理，因为P2、P3和P4在影响流行度的过程中权重太低以至于没有考虑它们的必要。但从4.3节中得知不同演化模式都因代表不同状态而存在，因此考虑这4类常见演化模式并没有问题。方法2在处理演化模式这一类隐式特征的方法有待优化，因为：

Fig.7 Explicit feature weights of method 2 vs.benchmark studies图7 方法2与基准研究的显式特征权重对比

（1）P1出现最为频繁导致其特征值远远超过P2、P3和P4的特征值。P1作为最常见的模式，叠加式统计出现次数和整体归一化的计算方法无疑缩小了原本就出现次数较少的P2、P3和P4这3类演化模式间的差异。

（2）不同演化模式本身的影响和作用并没有单独量化。方法2中简单地用0/1来表示在某一时间点下某种演化模式是否出现，这基于一项基本假设：任意一个演化模式对APP未来流行度的影响只与其在生命周期中出现的次数有关，而与演化模式的不同种类无关。

（3）演化模式的持续时间各不相同。在4.3.4小节中明确指出模式的持续时间，并且不同演化模式的持续时间的差异显然是不能粗略认为是等同的。

因此需要针对方法2中不同演化模式的同种量化方法进行改进。

方法3叠加式持续时间序列

方法2认为演化模式这种隐式特征可以量化为两种统计数值的乘积：某种演化模式的影响力和它在生命周期中出现的次数。这里可以选取演化序列中统计的演化模式的持续时间来表征不同演化模式对于APP 未来流行度的影响，显然这两者确实是直接相关的，并且持续时间是由统计工作得到，本身能够较为客观地反映演化中的复杂影响。

采用累加式持续时间来表征隐式特征P1至P4的数值。这里继续采用数值矩阵表示，仍以一天时间为单位，即每过一个时间单位，若某种演化模式仍在持续就在数值上叠加1。例如演化模式P3在某个APP的生命周期中持续8天，则这8天内隐式特征P3的取值为（1，2，3，4，5，6，7，8），当然在统计工作结束后需要对隐式特征的取值统一归一化。这里采用LR和RF两种算法分别针对新的数据集进行训练并输出预测结果，同时计算测试集与预测集之间MSE 取值来衡量模型的精度。

图8显示了集中于前40%时间段内的数据的详细分析。其中横坐标表示预测集中的周序号，纵坐标表示预测的优化率与失误率，优化率定义为方法3中模型预测后成功降低原始模型（只考虑显式特征）MSE数值的百分比，而失误率则代表方法3模型与原始模型相比MSE 反而升高的百分比。可以清楚看到，方法3模型除了在初始周的优化率达到100%，最高优化率出现在第8周，之后便逐渐降低，在第20周甚至小于50%；相反的是，其失误率从第9周开始逐周增长，且具有持续增长的走势。

Fig.8 Accuracy of top 40%data prediction result in method 3图8 方法3前40%数据预测结果准确率

通过对方法3的细致分析，认为改进的模型相比原始模型确实能够有效降低MSE 数值，这说明将演化模式量化为持续时间着实是正确的。但新模型的优化性能却因APP生命周期的推移而受限。这里尚待商榷的因素还有一个：持续时间的累加程度。方法3将某一天的演化模式表征为之前所有持续时间的加和，这存在前提假设：之前所有的演化模式的出现都对未来流行度产生相同程度的影响。显然这不够合理，例如100天前的演化模式的构成比例对于当前的流行度的影响十分微妙。因此再次对模型进行改进，提出方法4。

方法4时间窗口式持续时间序列

设置滑动时间窗口，每次选取固定时长的演化特征的取值来引入模型。也就是说，在每天特征中，演化模式处的4个特征值分别为之前42天（6周）的持续时间的叠加值。分别计算不同时间窗口下对应模型的优化率，实验结果如图9所示。

Fig.9 Accuracy of prediction results in method 4图9 方法4预测结果准确率对比

由图9可知，当时间窗口为4周时方法4的优化率能够达到最高为85.7%。

7 总结与展望

本文采集大量APP 群智感知数据，通过对APP流行度演化曲线的切割与聚类归纳出7种原子演化结构；之后通过序列模式挖掘发现APP 流行度演化过程的6种基本演化模式；针对统计数据分析后，探究了影响APP 流行度演化的7种影响因素：更新动作、营销活动、同类APP 数量、实时排名、评论量、评分和评论情感。之后将演化模式与7种影响因素结合，针对其内源性联系和相互影响进行探究并得到一系列普适结论；之后本文提出预测APP流行度演化的CrowdPop 模型，模型采用随机森林算法，将演化模式的组成与作用以及探索得到的7种影响因素归纳并量化为8种特征数据作为预测因子，并提出量化演化模式的4种不同方法并与其他两种算法进行对比，实验证明，CrowdPop模型能够有效提高预测精度。

本研究中仍有很多问题值得继续探索，例如扩展CrowdPop 预测模型，通过引入更加细粒度的APP使用数据作为预测因子来提高预测精度，并针对不同类型、不同市场排名等分类方式细化CrowdPop 模型，训练APP不同标签的特征参数，使预测模型针对性更强且又涵盖全面。