基于Voronoi划分的位置数据KNN查询处理方法*

宋宝燕，孟彦伟，丁琳琳

辽宁大学 信息学院，沈阳 110036

1 引言

空间数据描述了实体对象的形状、位置等属性信息，广泛应用在社交网络、物流系统等领域[1]。随着计算机技术和位置数据采集技术的愈发成熟，位置数据的规模急剧增长，且不断随机变化。K最近邻（K-nearest neighbor，KNN）查询是空间数据查询的重要研究内容。

Fig.1 Take-out service图1 外卖服务图

图1表示外卖服务的场景。在外卖服务中，假设d1、d2、d3配送员同时接收到store 和business 和其余很多商家发送的订单消息，d1、d2、d3配送员如何快速地从多个消息中找出与商家距离最近的K个订单进行派送，即KNN查询问题。然而，位置数据是不断随机变化的，该区域内的配送员数量是随机增加和删除的，同时某一时间段内，需要派送的商家和数量也是变化的。面对这些海量、随机变化的位置数据，目前的KNN 查询方法面临查找和更新间的失衡问题[2-4]，不能及时地给出有效的查询结果。如何更高效、准确地处理KNN查询成为了研究重点。

本文借助于Voronoi 图[5]在空间区域划分方面的优势，提出了一种基于Voronoi划分的位置数据KNN查询处理方法，解决了大规模位置数据的KNN 查询问题。首先，针对数据的原有性保持问题，提出了基于K-means算法的位置数据重新分布方法，实现了空间数据的不完全聚类。其次，提出了一个二级空间索引结构——VRI（VHash and VR index），包含VHash（Voronoi Hash）和VR（Voronoi and R）树两部分。一级索引结构VHash 表示Voronoi 图的直邻，二级索引结构VR 树，按照各Voronoi 单元所在的最小矩形区域的重叠面积，自下而上地生成对应的R 树。再次，基于VRI索引结构提出了位置数据的KNN查询算法及动态维护算法，采用VR树进行定位，VHash查找K近邻，能够有效地对查询点定位，查找速度快。最后，针对数据更新的情况，索引结构也能够及时更新，在更新的时间段内，对于位置数据随时间变化的KNN查询，提出了利用记录表进行有效查询的方法。

2 相关工作

2.1 分布式空间索引结构

目前，关于分布式空间索引技术的研究取得了一定的研究成果。文献[6]提出了基于空间填充曲线网格划分的最近邻查询算法，该算法解决了R树变体中的区域重叠现象，但破坏了数据的原有性，未能使位置更近的中间节点组合，导致查询结果的不准确和查询效率低。文献[7]提出了基于R树索引的内容地址网络（R-tree based index in content addressable network，RT-CAN）的空间索引结构，即一种基于路由协议的CAN 索引技术[8]和基于R 树的索引技术的结合体。这种空间索引结构，在处理少量高维数据查询时具有一定的优势，但是在处理海量空间数据时，存在查询与更新失衡的问题。文献[9-10]提出了并行的空间查询处理算法，提高了查询处理的效率，但是查询采用自上而下地遍历索引结构的方法导致根节点及靠近根节点的中间节点的负载量过大的问题。文献[11-12]提出了一次性的空间索引方法，使用一个分离的内存数据结构跟踪这些数据的变化，通过延时更新来缓解更新的高负载问题。这两种索引结构都需要维护一个更新跟踪缓冲区，该缓冲区存储了全部数据的有序的更新，并用于缓冲区和基础的空间索引结构交换对象。文献[13]提出了一种基于Voronoi的Merkel R树(Merkel R-tree，MR-tree)索引，实现了区域覆盖的最小化，但该索引在的划分方法，未能保持数据的原有性，中间节点间区域存在区域覆盖及未能将距离近的中间节点区域结合的问题。

2.2 KNN查询

KNN 查询问题也取得了很多研究成果。文献[14]提出了改进的增量最近邻查询算法，该算法是通过一定的内存资源代价，减少最近邻居查询索引遍历过程中的时空运算次数，但在复杂空间数据和高维空间中，还是具有一定的空间代价。文献[15]提出了基于Δ-tree 的自底向上的KNN查询算法，该算法使用类似Δ-tree 中节点生成方法确定查询点在Δ-tree 中所隶属的叶子节点及其所有祖先节点，但存在索引结构的更新与查询失衡的问题，并且在处理大量随机变化的空间数据时效率较低。文献[16]提出了将KNN 查询转换为多个区域查询的方法，在进行区域查询时，利用查询点与关键点间的距离逐层缩小查询空间，提高了查询的效率，但区域查询的初始半径和查询半径的增大速率有待进一步提高。文献[17]以Voronoi 单元代替最小边界矩形，自下而上地生成了一种新的空间索引结构——VR树，避免了基于R树及其变体空间索引结构中的区域覆盖问题，提高了查询的效率，尤其是1NN 查询，但该索引结构适合静态的空间数据，不适宜动态、随机变化的位置数据。

3 Voronoi划分的空间索引

二级索引结构包括VHash表和VR树，形成了二级索引结构——VRI。

3.1 分布式Voronoi空间划分

3.1.1 重新分布

位置数据一般是随机分布在若干服务器中，这种存储没有考虑到位置数据的相对位置、距离等，而KNN 查询是依据位置数据的相对位置和距离完成的。为了保持数据的原有性，即位置数据的相对位置和距离，本文对需要随机分布的位置数据进行重新分布。

K-means 算法[18]通常是依据位置数据间的欧式距离聚类的，聚类后可以保持这些数据间的相对位置。本文采用K-means算法聚类时，首先将具有经纬度的位置数据映射为欧式空间数据，选择的聚类中心个数是服务器数量S，迭代次数是依先验知识设定的，此迭代计算进行聚类，聚类后，每个服务器存储一个聚类结果与对应的聚类中心。

仍以图1中例子进行说明，某一时刻，随机选取11个有订单需求的商家，其位置在欧式空间中的表示如图2所示。

随机分布的位置数据进行重新分布前后的存储结果，如图3所示。

3.1.2 初始Voronoi

Fig.2 Euclidean representation of location data图2 空间数据欧式图

Fig.3 Schematic diagram of redistribution data图3 数据重新分布示意图

Voronoi 图是依据欧式距离进行空间区域划分的，可将空间划分为相邻而互不重叠的区域，隐含地构建了离散点之间的邻近关系，可有效支持K近邻的快速查找。本文对每个服务器上重新分布的位置数据创建局部Voronoi图。

各个服务器中，这种局部Voronoi 图的创建采用多核技术和改进的扫描线算法[16]并行生成。各服务器中生成的初步局部Voronoi 图如图4所示。图4中的1到11为位置数据的欧式表示，也是原始生成点，原始生成点所在的多边形为Voronoi单元，在S1服务器中，L2、L3为S1、S2服务器的边界点。

Fig.4 Initial local Voronoi diagram of each server图4 各服务器的初始局部Voronoi图

3.1.3 Voronoi优化

在各服务器初步生成的局部Voronoi 图中，没有考虑服务器边界点间的影响关系，导致生成的局部Voronoi图是不准确的。

为了优化不准确Voronoi 单元的数量，找出每个服务器上的聚类中心，聚类中心代表各服务器上的聚类结果，而各个服务器中的聚类中心可能是不存在的位置数据，本文选取距离聚类中心最近的位置数据代表各个服务器中的聚类结果。

定义1（近心点）给定各服务器重新分布的位置数据O及个数n和各服务器聚类中心C及个数s，对于各服务器任意的，即oy为近心点。

Voronoi 优化的一个方面是近心点优化，近心点优化可以利用空间复制技术实现。首先，根据近心点生成Voronoi 边界，S1、S2、S3服务器间的Voronoi边界如图5所示，再由先验知识设定边界点到边界的距离，即边界距离，计算各边界点到边界的距离，得计算后的距离。将计算后的距离与边界距离比较，当计算后的距离小于等于边界距离时，则将该边界点复制到有影响的服务器中，在各服务器中并行地完成上述过程，即实现了近心点的优化。优化后的结果如图6所示，其中下划线标识数据为需要复制的位置数据。

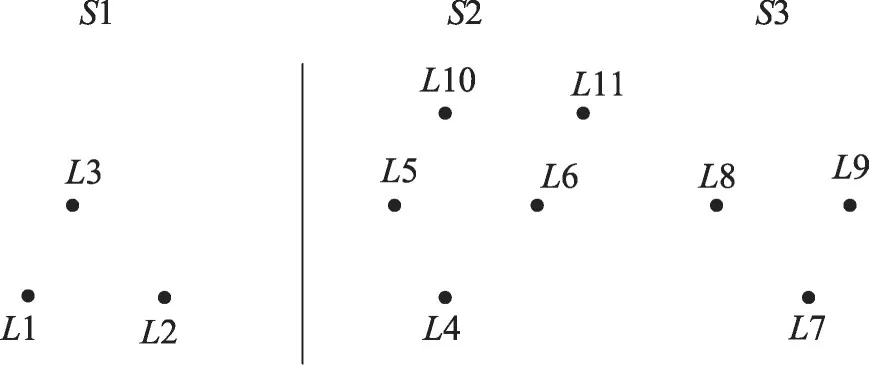
Fig.5 Voronoi boundary图5 Voronoi 边界

Fig.6 Close heart point optimization of data graph图6 近心点优化数据图

Voronoi 优化的另一个方面是不准确Voronoi 单元的识别和修复，利用影响区域[18]对各服务器边界点所在的Voronoi 单元进行识别和修复，从而生成正确的局部Voronoi图。如图7为优化后生成的正确的局部Voronoi图。

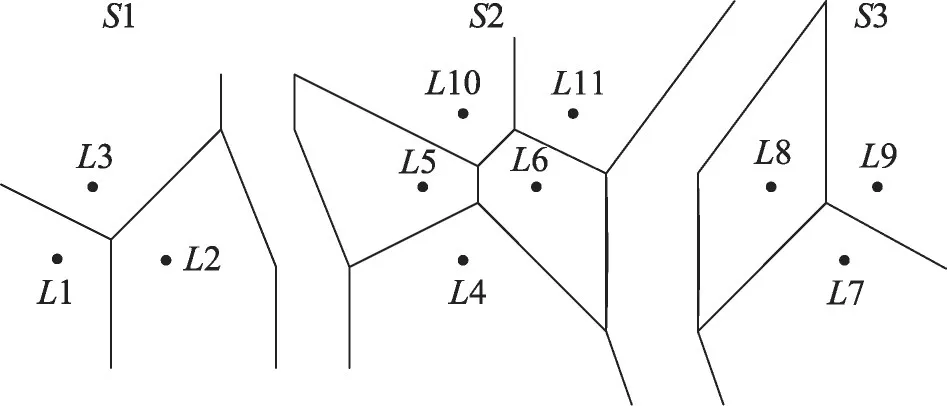
Fig.7 Local Voronoi diagram of each server图7 各服务器的局部Voronoi图

3.1.4 局部Voronoi的直邻表示——VHash

定义2（直邻表示）给定一Voronoi图VG，VG中的Voronoi 单元为VC，对于任意VC ∈VG，具有共享边和共享顶点VC 的生成点为该VC 的直接邻居，存储在哈希表中。

Voronoi 图可表示邻居间的关系，根据优化后正确的Voronoi 图生成直邻表示——VHash，作为一级索引结构，直邻表示不仅支持1NN查询，还支持KNN（K≠1）查询。

Fig.8 Voronoi schematic diagram图8 Voronoi示意图

由于映射快，方便查找，VHash采用Hash表进行存储，本文直邻表示存储的是具有共享边和共享点的生成点。如图8中，查询点q为配送员的位置，其余为需要派送订单的商家的位置，当配送员选择多个派送订单时，在第二个订单的选择时，若只考虑共享边为其邻居的因素时，在o2的邻居中，配送员位置q到o1的距离最近，因此配送员需要派送的第二单为o1，而实际存在配送员位置q到商家o4的距离小于到o1的距离。只考虑共享边会导致查询结果的不准确，因此本文选取具有共享边和共享点的生成点为直邻判断的依据。

表1～表3分别为各服务器中对应的直邻表示，在VHash 中，存储的是Object 和Neighbors，Object 为原始生成点，Neighbors为原始生成点的直邻。

Table 1 S1 VHash表1 S1 VHash

Table 2 S2 VHash表2 S2 VHash

Table 3 S3 VHash表3 S3 VHash

3.1.5 Voronoi划分后的全局信息

在经过位置数据的重新分布，初始Voronoi 图的生成和近心点Voronoi 的优化后，各个服务器完成了分布式的Voronoi划分，各个服务器存放的信息是（重新分布后的位置数据，边界点，近心点，VHash 表）。这些信息的全局概要，即全局信息，为各个服务器的（邻居，近心点）信息。通过全局信息，获得各服务器的相对位置和服务器间的Voronoi 边界，方便了优化和查找。

3.2 Voronoi划分的R树索引

3.2.1 Voronoi单元的最小矩形覆盖

在正确的Voronoi图中，找到能够覆盖Voronoi单元所在的最小矩形区域，并用横纵坐标的区间进行表示，即Voronoi单元所在的最小矩形区域。

3.2.2 组合表示（VR）生成

定义3（组合区域）给定一Voronoi 单元覆盖的最小矩形区域MR，将MR任意组合，将重叠面积大者任意组合，形成组合区域。

组合表示是按照Voronoi多边形所在最小矩形区域重叠面积的大小组合生成的，而重叠面积反映了对应Voronoi 多边形中生成点间的距离关系，将重叠面积较大的区域组合，减少了组合表示的数量，并使距离近的位置数据组合在一起。

由此，在找到每个Voronoi 单元所在的最小覆盖矩形区域后，将这些区域随机地组合，找出这些组合区域的重叠面积，重叠面积比较大者为一个组合表示，再找出已经生成的组合表示所在的最小覆盖矩形区域。同样，将这些区域随机地组合，找出重叠面积较大的组合区域，为新生成的组合表示，以此迭代地进行，直到新生成的一个组合表示中覆盖了服务器中所有的原始生成点，由此自下而上地生成了一个二级索引结构——VR树，如图9所示。

Fig.9 VR tree index structure图9 VR树索引结构

VR 树是由根节点、中间节点和叶子节点组成的，其中叶子节点的存储结构为(object，VC，data)，object 为位置数据，即Voronoi 单元原始生成点，VC为所在Voronoi区域唯一标识，data为Voronoi区域存储的近似表示；根节点和中间节点的存储结构为(objects，child，VR，data)，objects 为组合区域的生成点，即组合生成点，child 为指向孩子节点指针，设定M为该节点存放的最大记录数，m≤M/2为该节点存放的最小记录数，则child指针的个数为[m,M]。

VR 树的主要实现步骤是将数据集中的每个位置数据所在Voronoi 单元的矩形区域，与具有共享边的Voronoi 单元所在矩形区域重叠的面积比较，选取最大的重叠面积，并记录对应的Voronoi单元；将所有的重叠面积快速排序，按照从大到小的顺序，两两组合，在组合过程中，删除已经组合的数据，依次组合。对于每个服务器中的数据集，调用此方法，生成对应的VR 树。算法1表示基于Voronoi 划分的R 树生成算法。

算法1基于Voronoi划分的R树生成

输入:各服务器中数据集Oi，总数据集O。

输出:VR树。

在算法1中，第3行至第6行为服务器中每个位置数据所在的矩形区域及重叠面积的初始化，时间复杂度为O(1);第7行至第17行为选取某位置数据与其具有共享边的Voronoi单元所在矩形区域的重叠面积的最大值，并记录其矩形区域，算法的时间复杂度为O(n)；第18行至第21行为每个服务器中所有位置数据对应的最大重叠面积，并记录该数据与其重叠面积最大的Voronoi 单元所在的矩形区域，完成了整个服务器中数据集的最大重叠面积。该算法整体的时间复杂度为O(n2)，第22行为快排，算法的时间复杂度为O(nlgn)，第23行至第28行为VR树非叶节点和叶子节点的生成，算法的时间复杂度为O(n2lgn)，第29行至第31行为每个服务器中数据集的遍历，由此整个VR树生成算法的时间复杂度为O(n3lgn)。

3.2.3 VR全局信息

在经过了Voronoi 单元的最小覆盖和组合表示后，各个服务器完成了基于Voronoi 划分的R 树索引——VR 树，各个服务器存放的信息是（最小矩形区域，组合区域）。这些分布信息的全局概要，即全局信息，为各服务器的根节点组合区域，通过根节点组合区域这个全局信息，获得各服务器的最小覆盖矩形区域。

3.3 二级索引动态维护

在现实世界中，位置数据是随时变化的，要实现索引结构跟随空间数据的实时变动是不可能的，而且索引的创建也需要时间，这种现象在生活中也可见到，如手机地图中人的位置信息并不是实时更新的，而是每隔一段时间更新，以此延长电池的使用寿命，因此本文每隔一段时间重新创建二级索引——VRI。

在位置数据变动不大的情况下，根据位置数据的变化进行数据的增加或删除，在新增位置数据中，需判断新增数据到各近心点的距离，以完成数据的重新分布。例如在外卖非高峰期时，因移动位置数据变化比较小，某一时刻需要发送订单的商家变化也不大，在偶数次索引创建时，可不用对发送订单的商家进行重新分布，只依据奇数次，即前一次索引创建的数据分布即可，缩短了索引的创建时间。算法2为索引创建算法。

算法2索引创建

输入：数据集O。

输出：二级索引结构。

在算法2中，第2行为生成局部Voronoi 图，第3行为生成VR 树，整个索引创建的时间复杂度为O(n4lgn)。

4 位置数据KNN查询

通过R 树确定查询点所在的Voronoi 单元，进一步通过VHash 获得KNN 查询结果；在VHash、VR 二级索引更新期间，针对变化的位置数据，实现了近似查询及精确查询。

4.1 KNN查询

4.1.1 查询点定位

全局信息可以确定查询点可能所在的服务器，而VR 树中的组合区域可以逐步缩小查找范围。在KNN查询中，首先结合全局信息，利用VRI索引中的VR树进行查询点的定位。

例如，假设服务器S1接到查询Q（包含查询点q和查询条件），S1服务器会判断查询点q是否在本服务器中，若查询点q在S1服务器中，则查询Q在服务器S1中进行处理；若查询点q不在S1服务器中，则S1服务器将查询Q发送至具有全局信息的服务器，该服务器将q的横纵坐标与存储的各服务器的根节点组合区域比较，得到查询点q可能所在的服务器，并将查询Q发送至可能所在服务器，在这些服务器中，并行地遍历VR树，找到查询点q所在的服务器，并将结果返回至全局信息服务器。

在确定查询点q所在的服务器后，在该服务器中，利用VR 树查找查询q所在的Voronoi 单元。在确定查询点q所在的Voronoi 单元时，自上而下地遍历VR 树。将q的横纵坐标与VR 树的组合区域比较，直到遍历整个VR树为止。找到查询点q可能所在的Voronoi单元，计算查询点q到这些Voronoi单元对应的生成点的距离，距离最短的生成点对应的Voronoi单元为查询点q所在的Voronoi单元。

4.1.2 近邻确定

VHash 是直邻表示，也就是生成点的直接邻居，即与该生成点有共享边的Voronoi单元的生成点。在确定查询点q所在的Voronoi单元后，根据Voronoi图中具有共享边的Voronoi单元的生成点间距离最近这一性质，可利用VHash 进行查询点近邻的确定。针对查询点q，其第一个近邻是所在Voronoi 单元的生成点，而q的第二个近邻在第一个近邻的邻居中，此时遍历查询点所在服务器的VHash索引，根据VHash可找出第一个近邻的邻居，并计算查询点q到这些邻居的距离，距离最短的为第二个近邻，依次迭代地进行，直到找到K个近邻为止。算法3表示KNN 查询算法。

算法3KNN查询

输入：空间数据集O，查询点q，整数K，VR树节点存储的Voronoi区域G，VHash。

输出：所有符合查询条件的数据对象。

在算法3中，第1行到第3行为查询点的定位，算法的时间复杂度为O(n3)，第4行为第1个近邻的查找，算法的时间复杂度为O(1)，第6行到第11行为剩余K-1个近邻的查找，算法的时间复杂度为O(n2)，因此算法的时间复杂度为O(n3)。

例如，在利用二级索引结构进行KNN查询时，查询Q：查询点q(13,1),K=3。需要在已知的11个需要发送订单的商家位置中，找出满足该查询条件的商家。

首先，结合VR树进行查询点q的定位。S1服务器接到查询Q时，S1服务器在本地将查询点q的横纵坐标与其最小覆盖矩形区域进行比较，得知查询点q不在本服务器中，则将查询Q发送至具有全局信息的服务器，全局信息服务器依据存储的根节点组合区域与q横纵坐标比较，得q在S2服务器中，将查询Q发送至S2。

在S2接收到查询Q后，将查询点q的横纵坐标与VR 树的组合区域进行比较，自上而下地遍历VR树，直到遍历结束，找到q可能在L4、L6、L11这三个生成点对应的Voronoi 单元中，计算q到这些生成点的距离，得知q到L6距离最近，即查询点q在L6这个Voronoi单元中。

在确定查询点q在L6这个Voronoi单元后，利用VHash 进行近邻的确定。依据Voronoi 图的性质，查询点q的第一个近邻为其所在的Voronoi单元对应的生成点L6；q的第二个近邻在第一个近邻的邻居中，在S2服务器的VHash 索引中，如表2所示的VHash中，找到L6的邻居。表2中，L6的邻居为L4、L5、L10、L11、L8、L7，比较查询点q(13,1)到这些邻居的距离，距离最短的L11为q的第二个近邻；同样，q的第三个近邻在6和11这两个生成点对应的Voronoi单元的邻居中，即在L4、L5、L10、L7、L8、L9中，找出q到这些点中距离最短的L4、L8为q的第三个近邻。由此，找到查询点q(13,1)的三个近邻，为L6、L11、L8或者L6、L11、L4。

4.2 动态维护

4.2.1 原始生成点结构扩展

各服务器中的位置数据是随时变化的，实时地增加或删除，针对这些动态变化的空间数据，要实现索引结构的实时更新是不可能的，需要一个记录表记录t+Δt时刻，每个服务器中位置数据的增加或删除情况。如表4为t+Δt时刻记录表，记录了各服务器某一时刻，需要发送订单的商家的位置变化情况。

Table 4 Record table for location data表4 位置数据记录表

在Δt索引更新期间，进行查询时，先在原索引结构中进行KNN查询，再利用t+Δt记录表和VR树进行近似查询和精确查询。

在动态维护中，为了实现近似查询和精确查询，需要对叶子节点的存储结构扩展，增加一个parent的指针，在回溯方法中便于找到上一层中间节点。

4.2.2 近似结果

当KNN查询结果只作为对整体趋势的一个参考时，已有的KNN查询结果即可满足需求，此结果为一级近似结果。

如上述例子中，KNN 查询结果为L6、L11、L8或者L6、L11、L4，则一级近似的结果为L6、L11、L8或者L6、L11、L4。

当依据KNN 查询结果确定其所在的区域时，利用回溯方法找到KNN查询结果对应的上一层节点区域，判断新增加的位置数据是否在该区域中，若在该区域，则保存，并删除已有结果中的位置数据，找出满足需求的一个二级近似结果。

如上述例子中，KNN 查询结果为L6、L11、L8或者L6、L11、L4，在进行二级近似查询时，只需要在VR树中找到L6、L11、L4、L8对应的上一层节点区 域，得 到(S2,R1)、(S2,R2)、(S2,R3)、(S3,R1)、(S3,R2)，而新增位置数据L12(13,3)在中间节点(S2,R1)和(S2,R3)中，L13(17,3)在中间节点(S3,R1)中，删除已经变化的空间数据L11和L8，可得二级近似查询结果为L8、L11、L12、L13。

4.2.3 精确结果

当根据KNN查询结果确定空间数据的具体位置时，如配送员在选择派送的订单时，需要对选择发送订单的商家位置有一个精确的结果时，需对KNN 查询结果变化数据进行查找和计算，找出满足需求的精确结果。首先在VR树中，利用回溯方法找到KNN查询结果对应的上一层节点区域，判断新增加的位置数据是否在该区域中，若在该区域，则保存，并删除已有结果中的空间数据；其次遍历VHash，找出前K-1个近邻的邻居；最后计算前K-1个近邻中不变的空间数据及邻居和记录的新增的空间数据到查询点q的距离，升序排序后，选择前三个生成点即为查找的三个近邻。算法4表示精确查询算法。

算法4精确查询

输入：KNN查询结果集kobject，记录表，VHash。

输出：符合变化的所有数据对象。

在算法4中，第1行为依据VR树，找到已有KNN查询结果的上层节点区域，算法的时间复杂度为O(n)，第2行至第3行找到在步骤1中区域的新增数据并记录，时间复杂度为O(n)，第4行至第5行为删除KNN查询结果k-1个近邻中位置变化的数据，算法的时间复杂度为O(n2)，第6行至第7行为计算查询点q到步骤5中数据的距离，并进行排序，算法的时间复杂度为O(n2)，第9行至第10行为选取前K个，算法的时间复杂度为O(n)，因此精确查询算法的时间复杂度为O(n2)。

如上述例子中，KNN 查询结果为L6、L11、L8或者L6、L11、L4，当查询只需要精确结果时，只需要在VR树中找到L6、L11、L4、L8对应的上一层节点区域，得 到(S2,R1)、(S2,R2)、(S2,R3)、(S3,R1)、(S3,R2)，而新增位置数据L12(13,3) 在中间节点(S2,R1) 和(S2,R3)中，L13(17,3)在中间节点(S3,R1)中，删除已经变化的空间数据L11和L8，在VHash 中找出前K-1个近邻的邻居，计算查询点q到L6、L4、L5、L10、L7、L8、L9、L12、L13的距离，升序排序后，前三个近邻为L6、L12、L4。

5 实验

5.1 实验环境

本实验环境为16台配备英特尔奔腾G3220双核处理器，4 GB内存，500 GB硬盘的计算机和16台具有4 GB内存的双核虚拟机，它们具有相同Ubuntu16.04操作系统，编程环境为Eclipse10.0，编程语言为Java，集群环境为hadoop2.6。

实验所用数据集如表5所示。

Table 5 Datasets table表5 数据集表

真实数据集为外卖服务（take-out service，TS）中数据集。数据集为1 827个配送员在一周的轨迹数据，包含了107万个坐标。在删除了方向、速度等因素后，筛选出了用户有效属性信息，共由bk id、date time、longitude、latitude这四部分组成，bk id为配送员的车辆编号，具有唯一性，对应配送员身份的识别，date time 为位置上传时间，longitude 为经度，latitude为纬度。随机选取其中84 h 的运动轨迹，并将这些数据按每10.5 h 为一个区间段进行分割，共分为8组，每组数据包含6.68万个坐标。把每个区间段的所有坐标进行重新标识，并使用mapgis 软件进行坐标的转换，作为每组的实验数据集。

模拟数据集（uniform dataset，UD）为含有x和y值的实体对象，随机生成100万个坐标作为空间实体对象。为实现数据集变化，对应的x和y值进行加减，实现数据集的更新。在100万个坐标中，随机选取6.68万个坐标为一个初始数据集，同时进行x和y值的加减操作，将数据更新，得到8组变化的数据集。

5.2 索引

本节实验通过改变服务器中数据集的变化幅度和集群中节点的数量在真实数据集和模拟数据集中进行实验，观察VRI索引的创建时间。

在通过改变数据集变化幅度来观察VRI、RTCAN和VoMR-tree创建索引的时间这一实验中，需要选取数据集的更新百分比为1%、5%、10%、15%、20%、25%、30%的7组数据集。在真实数据集中，以最初的实体对象为基础，统计每分钟内变化的实体对象的数量，并计算变化的实体对象的数量占初始的实体对象的百分比，选取变化百分比为1%、5%、10%、15%、20%、25%、30%的7组数据进行实验，观察VRI 和ToSS-it创建索引的时间。在虚拟数据集中，以最初随机生成的数据集为基础，分别选取占总数据集百分比为1%、5%、10%、15%、20%、25%、30%的7组数据集，并将每组数据集的x和y值进行加减，实现数据集的更新，以进行实验，观察VRI、RT-CAN和VoMR-tree创建索引的时间。其实验结果如图10和图11所示。

随着数据更新幅度的增加，VRI创建索引的时间总体趋于平稳，说明VRI索引结构都适应于随机变化的位置数据对象，基于K-means算法进行的不完全聚类比在随机选取的数据间的距离和大者为关键点聚类的效果好，减少了局部Voronoi 生成过程中消息传递的数量，提高了索引创建的效率；RT-CAN 索引结构随着数据更新幅度的增加，索引的创建时间增长较大。因为随着更新量的增加，传递消息的总量以将近7倍的数量在增加，少量的更新都可能导致R树的整体更新，所以RT-CAN索引结构不适应随机变化的位置数据；而VoMR-tree索引的创建时间随着数据更新幅度的增加而急剧增加，因为更新幅度的增加意味着需要增加或删除的数据增加，所需要的时间也就增加了。

Fig.10 Creation time of index with data updating in uniformed dataset图10 模拟数据集数据更新索引创建时间

Fig.11 Creation time of index with data updating in TS dataset图11 真实数据集数据更新索引创建时间

在通过改变集群中节点数量来观察索引创建时间这一实验中，在增加集群中节点数量的同时，需增加处理的实体对象的数量以进行实验，即在分割的16组数据随机选取需要的组数。在模拟数据集和真实数据集中，分别选取集群中4个节点、8个节点、16个节点和32个节点进行实验。其中对于真实数据集，在4个节点实验、8个节点实验、16个节点实验和32个节点实验中，其对应的数据集分别为1组数据集、2组数据集、4组数据集和8组数据集；对于模拟数据集分别生成与真实数据集中同等数量的数据集进行实验，然后观察索引的创建时间及变化曲线。如图12、图13为模拟数据集和真实数据集中，索引创建时间的变化曲线。

Fig.12 Creation time of index with changes of nodes in uniformed dataset图12 模拟数据集节点变化索引创建时间

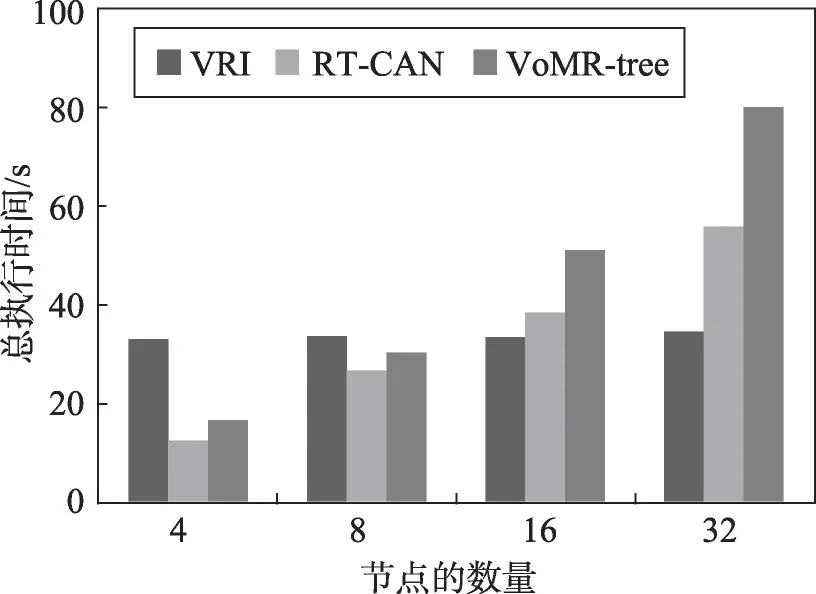
Fig.13 Creation time of index with changes of nodes in TS dataset图13 真实数据集节点变化索引创建时间

随着集群中节点数量的增加，VRI结构的创建时间基本没有明显的变化，而RT-CAN 和VoMR-tree 索引结构在创建时间上增长较快，说明VRI空间索引结构具有较好的性能，RT-CAN 和VoMR-tree 创建效率较低。同时，观察到VRI总的索引创建时间随着节点数量和数据集的增加，有一个稍微的增加，因为在数据重新分配阶段和R树生成阶段中，距离的计算和面积组合的计算需要稍长的时间。

5.3 查询

在评估KNN 查询算法性能这一实验中，通过改变K值和数据集的数量来进行查询性能评估。分别在真实数据集和模拟数据集中进行实验，观察KNN查询算法每秒处理的查询的数量的曲线变化，来对KNN查询算法的性能进行评估。

将整数K值在1到32之间进行变化，数据集不变，在真实数据集和模拟数据集中同时进行实验，观察每秒处理的KNN查询量。图14、图15为模拟数据集和真实数据集中，KNN 算法每秒处理的查询量随着整数K在1到32间变化的曲线。

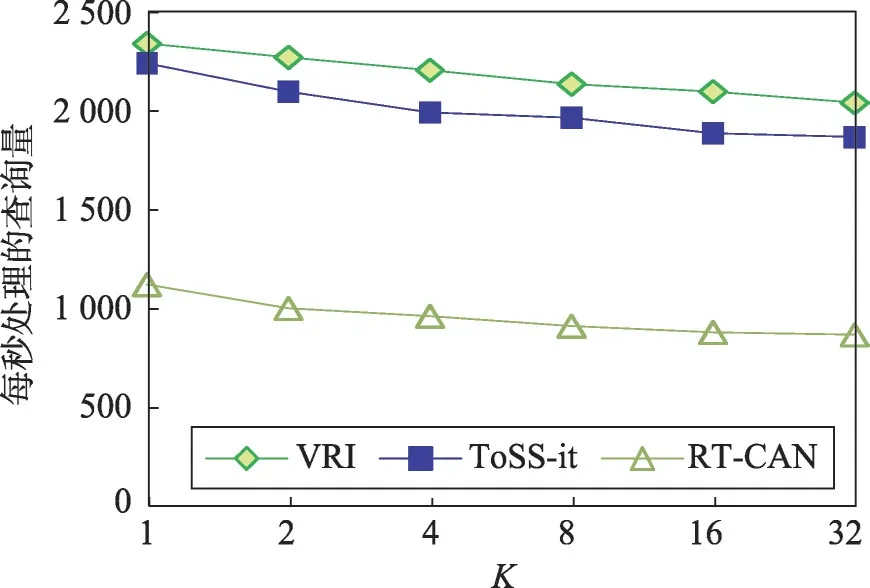
Fig.14 K value diagram in uniformed dataset图14 模拟数据集K值变化图

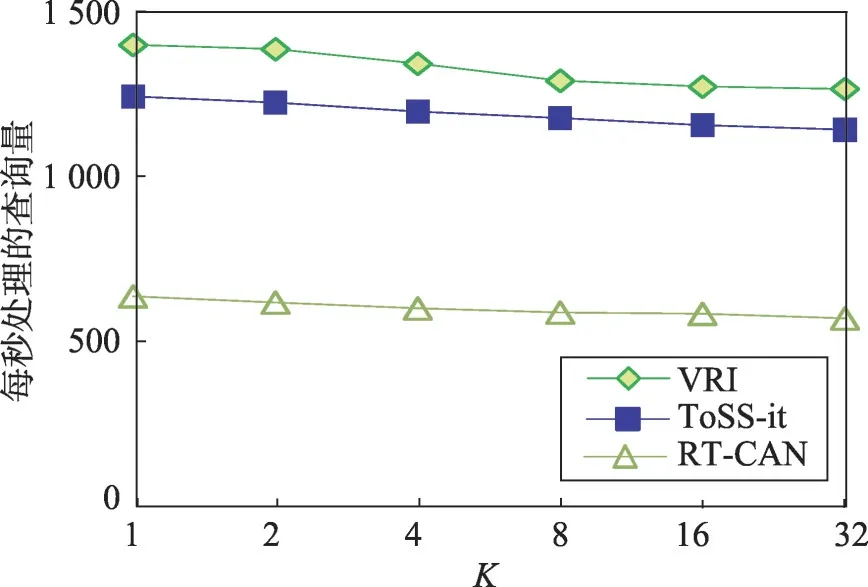
Fig.15 K value diagram in TS dataset图15 真实数据集K值变化图

两种数据集随着K值的增加，每秒处理的查询量逐渐减少，因为K的值增加，意味着在每个查询中，需要比较的实体对象的数量增加，从而增加了每个查询处理的时间，降低了查询的效率；VRI 索引结构中KNN查询处理速率高于ToSS-it和RT-CAN中的查询处理速率，而且模拟数据集中的处理速率高于真实数据集中的处理速率，即模拟数据集中KNN 查询算法的性能高于真实数据集中KNN查询算法的性能。

在确定K值之后，选取集群中节点数量为8，数据集组数分别为1组、2组、4组和8组进行实验，观察KNN 查询算法每秒处理的查询的总量。图16、图17为模拟数据集和真实数据集中，随着节点数量的变化，KNN查询算法每秒处理的查询量的变化曲线。

Fig.16 Data sizes diagram in uniformed dataset图16 模拟数据集数据量变化图

Fig.17 Data sizes diagram in TS dataset图17 真实数据集数据量变化图

同等条件下，随着数据集组数的增加，KNN查询算法每秒处理的查询量逐渐减少。在VRI中，数据集数量增加，意味着Voronoi图中的Voronoi单元数量增加，基于Voronoi图的R树中节点的数量增加，需要进行比较的区域和数据量增加，降低了KNN 查询的处理速率，而且模拟数据集中，KNN查询的处理速度高于真实数据集中的处理速度。

6 结论

随着位置收集技术的日渐成熟，移动位置数据爆炸式地增长，与之相对应的空间索引技术和查询方法也在不断地改进。KNN查询作为空间数据查询研究的重要内容之一，在现实生活中得到广泛应用和迅速发展。基于Voronoi 划分的位置数据的KNN查询方法，将VHash 和VR 树结合，构建了一个二级索引结构。其中，在一级索引结构VHash 创建过程中，基于K-means 的重新分布，保持了位置数据的原有性，且VHash 存储的是具有共享边和共享点的邻居，精确了查找；二级索引VR树，自下而上地进行节点结合，将重叠面积大者组合在一起，生成上层节点，由此实现了中间节点的聚类，加快查找，且弥补了R树变体空间划分中的兄弟节点交叠和覆盖问题，使查询路唯一，提高了查找效率。在KNN查询中，利用VR树进行查询点的定位，解决了频繁定位及定位时间长的问题，同时在索引更新期间，对KNN查询结果进行近似查询和精确查询，满足了多方查询需求，确保了查询的有效性。